最短路径算法小结

不同性质的图中，所采取的策略有所不同，自然存在各样的求最短路径的算法。

• 无向无权图：BFS
  
• 有向正权图：Dijkstra
  
• 有向无负环图：Bellman-Ford（单点），Floyd-Warshall(任意两点）
  
• 有向无环图（dags）： 基于动态规划的算法。

广度优先搜索（BFS）

对于无向无权图（也可以假设权值为1），就可以使用最基本的广度优先搜索算法，从源点开始对整个图进行搜索，访问到所有的点。因为广度优先搜索最先访问到的是相邻的点，所以距离最近的点最先访问到，记录的距离也就最小。

算法伪代码，时间复杂度为 $O(|V|+|E|)$。

for all u in V:
     dist(u) = INF

dist(s) = 0
Q = [s] (FIFO 队列)
while Q is not empty:
     u = eject(Q)
     for all edges (u,v) in E:
          if dist(v) = INF:
               inject(Q, v)
               dist(v) = dist(v)+1

Dijkstra 算法

Dijkstra 算法是基于广度搜索的单源最短路径算法，利用此算法可以在无负边的有向图中求得一点到图中其他点的最短路径。算法的基本思想是每个点记录源点到其他点的距离，在从以按距离值大小排列的优先队列中选取值最小的点，再更新相邻点的距离值，直到队列为空。

假设求点 s 到图中其他点的最短路径，$dist(u)$ 表示 s 到 u 的距离。 H 表示优先队列。
Dijkstra 算法伪代码表示如下

for all u in V:
     dist(u) = INF
     prev(u) = None

dist(s) = 0

H = makequeue(V) (using dist-values as keys)
while H is not empty:
     u = deletemin(H)
     for all edges (u, v) in E:
          if dist(v) > dist(u) + l(u,v):
               dist(v) = dist(u) + l(u,v)
               prev(v) = u
               decreasekey(H, v)

算法总共涉及 $|V|$ 次队列删除操作，$|V|+|E|$ 次队列插入和更新操作。如果优先队列的实现是基于二叉堆（binary heap）则队列插入和删除操作时间算法复杂度都为 $O(log|V|)$，算法的时间复杂度为 $O((|V|+|E|)log|V|)$。

Bellman-Ford 算法

Bellman-Ford 算法跟 Dijkstra 算法一样都是单源最短路径算法，但是可以应用于存在负边的有向图中。Dijkstra 算法中最关键的步骤就是当前距离值最小的点根据到相邻的点距离，更新相邻点到源点的距离，被选出的距离值最小的点的距离值是成递增关系。如果存在负边则前面已经被选为距离值最小的点的值可能改变，变得更小，也就使得 Dijkstra 算法不适用。

Dijkstra 算法的关键步骤是更新点到源点的距离值，更新按照距离值递增的顺序。如果存在负边就不能确保仍然按照这种递增的顺序更新，但最终仍是更新路径上所有点的距离值直到不再改变。一条最短路径最多经过|V|-1条边，所以 Bellman-ford 通过|V|-1次重复更新所有的边，来确保更新是按照正确的顺序进行。

如果图中不存在负环，则|V|-1次更新后，所有点的距离值都达到最小，不会再改变。存在负环的话，再进行一次更新，有的点的距离值仍然会改变。通过这种方法也可以判断图中是否存在负环。

算法伪代码如下，时间复杂度 $O(|V|*|E|)$

for all u in V:
     dist(u) = INF
     prev(u) = None

dist(s) = 0
repeat |V|-1 times:
     for all (u,v) in E:
          dist(v) = min{dist(v), dist(u)+l(u,v)}

动态规划算法

对于一个有向无环图，可以通过深度优先搜索获得其线性化顺序（linearised order），如下图

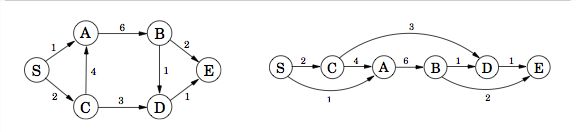
dist(u)表示从源点 s 到 u 的最短距离。求上图中的D点 的dist(D)，则只要知道跟 D 相邻并指向 D 的点的距离值（dist(B), dist(C)），通过比较取最小值：
$$ dist(D) = min\lbrace{dist(B)+1, dist(C)+3}\rbrace$$

要求得到某个点的最短距离前，要先求得到所有指向该点的最短距离。求解一个问题前，先要解决多个子问题，这也就利用了动态规范方法。
算法的伪代码如下，时间复杂度$O(|V|+|E|)$（DFS 获得线性化顺序的时间复杂度）。

for all u in V:
     dist(u) = INF
dist(s) = 0

LV = DFS(s) # linearised order

for v in LV:
     dist(v) = min{ dist(u)+l(u,v) for (u,v) in E }

Floyd—Warshall 算法

Floyd-Warshall 算法是一种基于动态规划的算法，利用此算法可以求得无负环有向图中任意两点间的最短路径。
无负环图中的点记为 $\lbrace{1, 2,...,n}\rbrace$，$dist(i,j,k)$ 表示 $i$ 到 $j$ 最短路径长度，路径经过的点只能是 $\lbrace{1,2,...,k}\rbrace$ 集合中的。

如何从 k-1个点扩展到 k 个点？

k 个点中，从 i 到 j 的最短路径只有两种可能，经过 k 点或不经过。如果经过 k 点，则以 k 为中间点，$dist(i,j,k)$ 可以表示为 $dist(i,k,k-1)$ 和 $dist(k,j,j-1)$ 的和值，如下图所示。

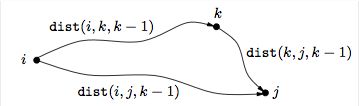
那么 dist(i,j,k)的值就为两条路径中值最小的一个。
$$min\lbrace{dist(i,k,k-1)+dist(k,j,k-1), dist(i,j,k-1)}\rbrace$$

算法伪代码表示如下，算法时间复杂度$O(|V|^3)$

for i=1 to n:
     for j=1 to n:
          dist(i,j,0) = INF
for all (i,j) in E:
     dist(i,j,0) = l(i,j)

for k=1 to n:
     for i=1 to n:
          for j=1 to n:
               dist(i,j,k) = min{dist(i,k,k-1)+dist(k,j,k-1), dist(i,j,k-1)}

参考资料

• Algorithms