切比雪夫滤波器的特性分析和设计

作者：Joseph Pan （转载请保留出处：http://www.cnblogs.com/weizhoupan/archive/2011/03/26/1996500.html）

一、实验背景

数字滤波器是DSP中非常重要的组成部分。滤波器有两种用途：分离混合的信号，复原失真的信号。在基频分析器中，伴奏是对人声的一种噪音干扰，因此需要尽可能减少噪音的影响。由于人的音高在300Hz~2000Hz之间，因此可以构造一个带通滤波器去除这个频段以外的信号。在常见的滤波器中，由于切比雪夫滤波器运算性能较好，且工作在频域上，因此最适合应用在基频分析器中。

 

二、实验目的

分析切比雪夫滤波器的特性，并完成切比雪夫系数的设计。

 

三、实验环境和工具

1. 实验平台：Windows
2. 开发语言：Fortran

 

四、常见滤波器的分类和切比雪夫滤波器的选择

根据应用场合和实现方式，常见滤波器可以如表1所示来进行分类：

	卷积	递归
时域	移动平均滤波器	单极点滤波器
频域	加窗sinc滤波器	切比雪夫滤波器
任意频响	FIR任意频响滤波器	迭代设计滤波器

表1 常见滤波器的分类

根据表1，由于基频的分析提取是工作在频域上的，因此滤波器主要在加窗sinc滤波器和切比雪夫滤波器两者间进行选择。根据系统的需求，为了实现快速获取基频分析结果，选择的标准主要取决于两者在速度上的优劣。

对加窗sinc和切比雪夫滤波器的速度的比较，即是对卷积滤波器（FIR）和递归滤波器（IIR）的比较。图1的曲线展示了加窗sinc滤波器和等效的6极点递归滤波器的相应执行时间。其中，标准卷积和快速傅里叶卷积是两种算法下构造的加窗sinc滤波器。加窗sinc滤波器的运行时间在低频和高频段上升，这是因为为了跟上递归滤波器在这些效率上更好的性能，必须增加滤波器内核的长度。总的来说，IIR滤波器要比相应的FIR滤波器快1个数量级。

图1 FIR滤波器和IIR滤波器的速度对比

 

五、切比雪夫滤波器的特性分析

切比雪夫滤波器（又译车比雪夫滤波器）是在通带或阻带上频率响应幅度等波纹波动的滤波器。在通带波动的为“I型切比雪夫滤波器”，在阻带波动的为“II型切比雪夫滤波器”。

1. 切比雪夫的频率响应特性

切比雪夫的频率响应如图2所示：

（a） 低通频率响应

（b） 低通频率响应（dB）

（c） 高通频率响应

（d） 高通频率响应（dB）

图2 切比雪夫频率响应

如图1所示，图a和图b是0.5%纹波的低通切比雪夫滤波器的频率响应，图c和图d是相应的高通滤波器的响应。

2. 阶跃响应的过冲

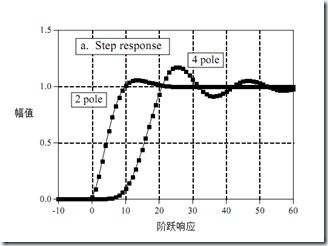
切比雪夫滤波器的阶跃响应有5%~30%的过冲，且随着极点数的增加而增大。图3是切比雪夫滤波器阶跃响应的两个例子。

图3 切比雪夫阶跃响应

3. 稳定性

递归滤波器运行很快，但在性能上受限。如果是低通高通滤波器，极点实际的数量将略微取决于纹波。单精度的近似数字如表2所示。

截止效率	0.02	0.05	0.10	0.25	0.40	045	0.48
最大极点数	4	6	10	20	10	6	4

当接近这一极限时，滤波器的性能将变差。阶跃响应将出现更大的过冲，阻带衰减将变差，频率响应将出现过多纹波。如果滤波器的设计指针太高，或系数中出现了错误，输出可能振荡直至有溢出发生。

为了增加极点的最大数目，以提高运算结果的准确性，可以采用分阶段实现滤波器，在本系统的基频分析模块中，我们将滤波器分为9级。如果每一级产生n个极点，则该滤波器将会产生9*n个极点的滤波器。

 

六、 切比雪夫滤波器的设计

递归滤波器是由差分方程描述的。

（1）

其中，x[]和y[]分别是输入和输出信号，a和b是递归系数。可以写成下面的形式：

（2）

滤波器的设计关键就在于a和b系数的获取。

递归系数可以使用下面的Fortran程序来获得：

   1: 100 'CHEBYSHEV FILTER- RECURSION COEFFICIENT CALCULATION

   2:  

   3: 110 '

   4:  

   5: 120 'INITIALIZE VARIABLES

   6:  

   7: 130 DIM A[22] 'holds the "a" coefficients upon program completion

   8:  

   9: 140 DIM B[22] 'holds the "b" coefficients upon program completion

  10:  

  11: 150 DIM TA[22] 'internal use for combining stages

  12:  

  13: 160 DIM TB[22] 'internal use for combining stages

  14:  

  15: 170 '

  16:  

  17: 180 FOR I% = 0 TO 22

  18:  

  19: 190 A[I%] = 0

  20:  

  21: 200 B[I%] = 0

  22:  

  23: 210 NEXT I%

  24:  

  25: 220 '

  26:  

  27: 230 A[2] = 1

  28:  

  29: 240 B[2] = 1

  30:  

  31: 250 PI = 3.14159265

  32:  

  33: 260 'ENTER THE FOUR FILTER PARAMETERS

  34:  

  35: 270 INPUT "Enter cutoff frequency (0 to .5): ", FC

  36:  

  37: 280 INPUT "Enter 0 for LP, 1 for HP filter: ", LH

  38:  

  39: 290 INPUT "Enter percent ripple (0 to 29): ", PR

  40:  

  41: 300 INPUT "Enter number of poles (2,4,...20): ", NP

  42:  

  43: 310 '

  44:  

  45: 320 FOR P% = 1 TO NP/2 'LOOP FOR EACH POLE-PAIR

  46:  

  47: 330 '

  48:  

  49: 340 GOSUB 1000 'The subroutine in TABLE 20-5

  50:  

  51: 350 '

  52:  

  53: 360 FOR I% = 0 TO 22 'Add coefficients to the cascade

  54:  

  55: 370 TA[I%] = A[I%]

  56:  

  57: 380 TB[I%] = B[I%]

  58:  

  59: 390 NEXT I%

  60:  

  61: 400 '

  62:  

  63: 410 FOR I% = 2 TO 22

  64:  

  65: 420 A[I%] = A0*TA[I%] + A1*TA[I%-1] + A2*TA[I%-2]

  66:  

  67: 430 B[I%] = TB[I%] - B1*TB[I%-1] - B2*TB[I%-2]

  68:  

  69: 440 NEXT I%

  70:  

  71: 450 '

  72:  

  73: 460 NEXT P%

  74:  

  75: 470 '

  76:  

  77: 480 B[2] = 0 'Finish combining coefficients

  78:  

  79: 490 FOR I% = 0 TO 20

  80:  

  81: 500 A[I%] = A[I%+2]

  82:  

  83: 510 B[I%] = -B[I%+2]

  84:  

  85: 520 NEXT I%

  86:  

  87: 530 '

  88:  

  89: 540 SA = 0 'NORMALIZE THE GAIN

  90:  

  91: 550 SB = 0

  92:  

  93: 560 FOR I% = 0 TO 20

  94:  

  95: 570 IF LH = 0 THEN SA = SA + A[I%]

  96:  

  97: 580 IF LH = 0 THEN SB = SB + B[I%]

  98:  

  99: 590 IF LH = 1 THEN SA = SA + A[I%] * (-1)^I%

 100:  

 101: 600 IF LH = 1 THEN SB = SB + B[I%] * (-1)^I%

 102:  

 103: 610 NEXT I%

 104:  

 105: 620 '

 106:  

 107: 630 GAIN = SA / (1 - SB)

 108:  

 109: 640 '

 110:  

 111: 650 FOR I% = 0 TO 20

 112:  

 113: 660 A[I%] = A[I%] / GAIN

 114:  

 115: 670 NEXT I%

 116:  

 117: 680 ' 'The final recursion coefficients are in A[ ] and B[ ]

 118:  

 119: 690 END

第270~300行，4个参数被输入到程序中。截止频率FC，被表达为抽样频率的分数形式，因此必须在0到0.5的范围内。变量LH，设置为1时对应高通滤波器，设置为0时对应低通滤波器。变量PR的输入值要在0到29之间，表示滤波器频率响应的纹波在0%到29%之间。滤波器的极点数通过变量NP输入，且必须是2到20见的一个偶数。程序运行完成时，a和b系数存放在数组A[]和B[]中（a0 = A[0]，a[1] = A[1]，等等）。

上面的程序只能用于获取高通或低通滤波器的系数，对于带通滤波器，则需要再进一步进行构造。在DSP系统中，带通滤波器可通过低通滤波器和高通滤波器级联而形成，如图4所示。

图4 级联构成的带通滤波器

图4所示的带通滤波器由一个低通滤波器和一个高通滤波器串联而成。设两个滤波器的系数分别为a₀、a₁、a₂、b₁、b₂和A₀、A₁、A₂、B₁、B₂，则整个系统的传递函数H[z]由两级传递函数相乘得到

（3）

进行多项式相乘和合并同类项后得到下面的形式

（4）

公式（4）符合公式（2）的形式，因此我们可以直接提取实现串联系统的递归系数

上面的计算过程可以交由计算机程序来实现。如下所示：

   1: 100 'COMBINING RECURSION COEFFICIENTS OF CASCADE AND PARALLEL STAGES

   2:  

   3: 110 '

   4:  

   5: 120 ' 'INITIALIZE VARIABLES

   6:  

   7: 130 DIM A1[8], B1[8] 'a and b coefficients for system 1, one of the stages

   8:  

   9: 140 DIM A2[8], B2[8] 'a and b coefficients for system 2, one of the stages

  10:  

  11: 150 DIM A3[16], B3[16] 'a and b coefficients for system 3, the combined system

  12:  

  13: 160 '

  14:  

  15: 170 'Indicate cascade or parallel combination

  16:  

  17: 180 INPUT "Enter 0 for cascade, 1 for parallel: ", CP%

  18:  

  19: 190 '

  20:  

  21: 200 GOSUB XXXX 'Mythical subroutine to load: A1[ ], B1[ ], A2[ ], B2[ ]

  22:  

  23: 210 '

  24:  

  25: 220 FOR I% = 0 TO 8 'Convert the recursion coefficients into transfer functions

  26:  

  27: 230 B2[I%] = -B2[I%]

  28:  

  29: 240 B1[I%] = -B1[I%]

  30:  

  31: 250 NEXT I%

  32:  

  33: 260 B1[0] = 1

  34:  

  35: 270 B2[0] = 1

  36:  

  37: 280 '

  38:  

  39: 290 FOR I% = 0 TO 16 'Multiply the polynomials by convolving

  40:  

  41: 300 A3[I%] = 0

  42:  

  43: 310 B3[I%] = 0

  44:  

  45: 320 FOR J% = 0 TO 8

  46:  

  47: 330 IF I%-J% < 0 OR I%-J% > 8 THEN GOTO 370

  48:  

  49: 340 IF CP% = 0 THEN A3[I%] = A3[I%] + A1[J%] * A2[I%-J%]

  50:  

  51: 350 IF CP% = 1 THEN A3[I%] = A3[I%] + A1[J%] * B2[I%-J%] + A2[J%] * B1[I%-J%]

  52:  

  53: 360 B3[I%] = B3[I%] + B1[J%] * B2[I%-J%]

  54:  

  55: 370 NEXT J%

  56:  

  57: 380 NEXT I%

  58:  

  59: 390 '

  60:  

  61: 400 FOR I% = 0 TO 16 'Convert the transfer function into recursion coefficients.

  62:  

  63: 410 B3[I%] = -B3[I%]

  64:  

  65: 420 NEXT I%

  66:  

  67: 430 B3[0] = 0

  68:  

  69: 440 ' 'The recursion coefficients of the combined system now

  70:  

  71: 450 END 'reside in A3[ ] & B3[ ]

在本系统中，选用44100的采样频率，高通频率为30Hz，低通频率为2Khz，为了获得更快滚降特性，选用4%的纹波。使用上面的程序获得a、b系数如下：

	A	B
0	9.684457e-07	0
1	6.779120e-06	-7.616874e+00
2	1.936891e-05	2.634041e+01
3	2.711648e-05	-5.424242e+01
4	1.355824e-05	7.325881e+01
5	-1.355824e-05	-6.726091e+01
6	-2.711648e-05	4.196424e+01
7	-1.936891e-05	-1.715111e+01
8	-6.779120e-06	4.166027e+00
9	-9.684457e-07	-4.581673e-01

七、实验总结

通过本实验，我们深入了解了切比雪夫滤波器的特性，并成功构造了一个4%纹波的切比雪夫带通滤波器，以提高基频提取结果的正确性。

参考文献：

[1] Steven W.Smith. Digital Signal Processing: A Practical Guide for Engineers and Scientists.[M] California Technical Publishing, 2003

感谢：

Special thanks to Steven W.Smith for his great tutorial and craigeaton for the parameters data in his project.