数据聚类综述第5章——聚类技术
原文:A.K.JAIN,M.N.MURTY和P.J.FLYNN所写的Data Clustering:A Review的第5章,本文系毕业设计时与搭档的外文翻译。转载请说明出处。前7节(11页)由搭档翻译,后5节(12页)由我翻译。
5. 聚类技术
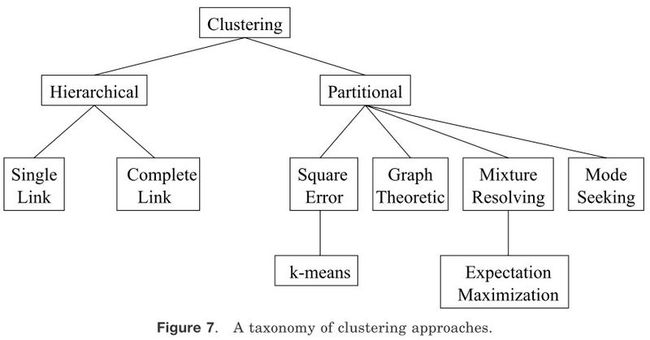
不同的文本聚类技术可以用图7的层次图来加以描述(其它对于聚类方法的分类描述也是可以的;我们的方法是基于在Jain和Dubes的描述[1988])。在顶层,层次聚类和划分聚类有所不同(层次聚类产生一系列嵌套的分区,而划分聚类产生只一个分区)。
在图7中显示的分类必须以跨领域的问题讨论作为补充,这些问题可能会影响所有分类方法,不管它们在分类法中的位置如何。
图7 聚类方法分类
——聚合VS划分:这方面涉及到算法的结构和运行。一个聚合方法开始时,每种模式都在一个独立的(单一的)类中并且此后持续的合并类在一起知道某一个停止条件被满足。一个划分方法开始时,所有的模式都是在一个类中,并以此为基础进行分裂知道某个停止条件被满足。
——单元VS多元:这方面涉及到在聚类过程中文本特征的连续或关联应用。大部分的算法是多元的;也就是说所有的特征都进入到特征之间距离的计算,并且结论是以这些距离为基础。在安德伯格会议上[1973]的一个简单的单元算法是循序的考虑文本特征来划分给定模式的集合。这在图8中有阐明,根据特征x1把集合分为两组;垂直的虚线是一个分割线。每一个分组有根据特征x2划分为独立的分组,如图虚线H1和H2所示。这种算法最主要的问题是会形成2d个聚类(d是模式的维度)。当d的值很大时(信息检索应用中一般使用d>100[Salton 1991]),聚类结果如此巨大以至于数据集被分成没有意义的小碎片。
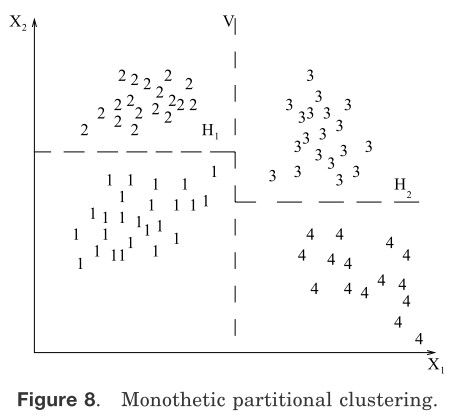
图8 单元分割聚类 图9三个聚簇中的点
——精确VS模糊:硬聚类算法在执行和它的输出中会把每一个模式分配给唯一的聚类结果。一个模糊聚类会根据隶属程度把一个模式划分到几个类当中。模糊聚类可以通过把模式划分到最大隶属程度的类中的方式转换为硬聚类。
——确定性VS随机: 这个问题和为优化方差函数的分割方法联系最紧密。最优化可以通过传统的技术或者通过一个针对包含所有标签的状态空间的查询。
——增量VS非增量:当用于分类的模式集很大时并且受到执行时间的限制或者内存空间的影响算法的体系结构时,这个问题就会产生。早起的聚类方法论不包含一些用于大数据集的算法的例子,但是数据挖掘的出现促进了聚类算法的发展,这些算法通过模式集合使扫描达到最少,在运行过程中减少对模式的检测或减少算法操作中的数据结构尺寸。
Jain和Dubes[1988]切实观察到聚类算法的规范化常常会为实现留出灵活性。
5.1. 层次聚类算法
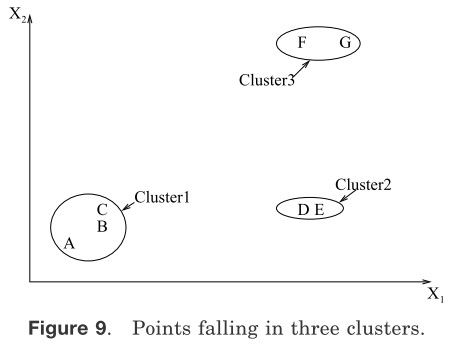
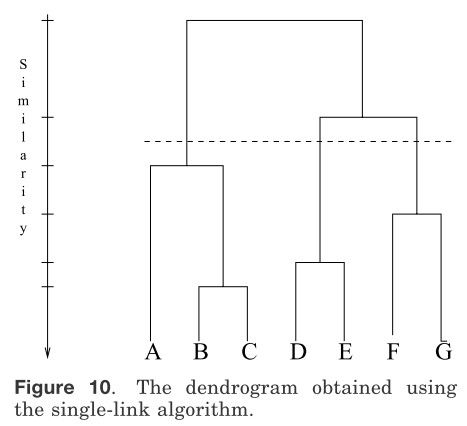
图9中用二维数据集阐明了层次聚类算法的操作。这个图形描述了七个特征标签A、B、C、D、E、F和G在3个聚类中。一个层次聚类算法生成 一个树来表示嵌套的分组模式和相似的水平在分组内改变。一个生成树和图九中相一致的七个点(从Jain和Dubes单连接算法得到)在图10中表示。生成树可以被分成不同的层次来表不同的聚类子集。
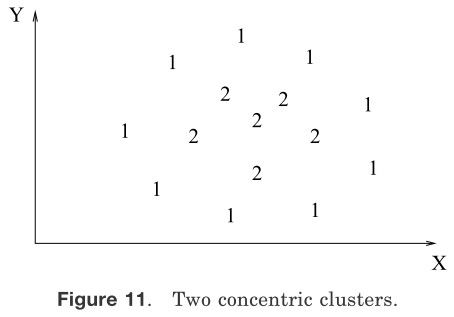
大部分的层次聚类算法是单连接层次算法[Sneath 和Sokal 1973]、全连接[King 1967]和最小方差连接算法[Ward 1963;Murtagh 1984]的变形,其中单连接和全连接是最常用的。这两种算法在描述相似群集的方法上不同。在单链接方法中,两个聚类的距离用聚类之间所有模式距离(一个模式来自一个聚类,另一个模式来自另外一个聚类)的最小值来表示。在全连接算法中,聚类之间的距离是两个类中相距最远的两个对象的距离。在这两种情况下,两个较小聚类合并成为一个大的聚类是基于最短距离标准。全连接算法产生紧密牢固或者紧凑的聚集。与之相比,但连接算法则受到连接的影响[Baeza-Yates 1992].可能会倾向于产生散乱或者瘦长的聚类集合。在图12、图13中有两个聚类集通过噪音模式被分割。单连接算法产生的聚类在图12中表示,而全连接算法的结果在图[13]中表示。全连接算法获得的聚类结果比但连接算法的聚类结果更紧凑;由但连接获得的标签为1的聚类是瘦长的,这是因为标注为“*”的噪音模式。然而单连接算法比全连接算法更灵活。例如,单链接算法可以提取如图11所示的同中心的聚类,但是全连接不能。然而,从现实应用来看,全连接算法在许多应用当中能比单链接产生更有用的分类[Jain 和Dubes 1988]。
图12 两个以噪声(*)相连的类(1和2)的单链接聚类 图13 两个以噪声(*)相连的类(1和2)的全链接聚类
凝聚的单链接聚类算法
(1)把每一个模式放到自己的聚类当中。构建一个基于双模式的无序对序列并按降序排列。
(2)遍历分类距离列表,形成每一个不同的距离值dk模式曲线,在这个曲线里模式对里距离权值小于dk的形成连接区域。如果所有的模式都是属于一个连接区域,则停止,否则继续上述操作。
(3)算法的输出是一个嵌套的层次图,在相应的图表中通过简单连通分量,这个层次图可以按照所希望的相异水平划分为不同的区域(聚类)。
凝聚的全连接算法
(1)把每一个模式放到自己的聚类当中。构建一个基于双模式的无序对序列并按降序排列。
(2)遍历分类距离列表,形成每一个不同的距离值dk模式曲线,在这个曲线里模式对里距离权值小于dk的形成连接区域。如果所有的模式都是属于一个连接区域,则停止,否则继续上述操作。
(3)算法的输出是一个嵌套的层次图,在相应的图表中通过完全连通分量,这个层次图可以按照所希望的相异水平划分为不同的区域(聚类)。
层次聚类算法比划分聚类算法更加灵活。例如,当数据集包含各向异性聚类包括良好分治、相似链和同心数据集时但连接算法工作很好,然而一个典型的划分算法例如K-means只有当数据集有各向同性[Nagy 1968]时工作良好,另一方面,划分算法的时间和空间复杂度[Day 1992]明显比层次聚类算法要低。利用两种方法的共同优点开发包含混合聚类算法[Murty和Krishna 1980]是可行的。
层次凝聚聚类算法
(1)算出包含每对模式指间距离的邻接矩阵
(2)在邻接矩阵中找到距离最小的聚类对。把这两个聚类合并为一个聚类。通过合并操作更新邻接矩阵。
(3)如果所有的模式都在一个聚类中,则停止,否则,继续第2步操作。
基于第二步更新邻接矩阵的方法,可以设计出多种的凝聚算法。层次划分算法以一个包含所有元素的聚类作为开始,并且给予一定的规则持续的对聚类进行分割得到单一聚类集的一个划分。
5.2. 划分算法
划分聚类算法得到数据的一个单独的划分,而不像层次算法产生系统树那样产生一个聚类结构。划分算法对于那些构造系统树时受到计算能力限制时的大数据集应用中有优势。伴随着划分聚类算法应用产生的一个问题是期望得到的数据集数目的选择。一个优秀论文[Dubes 1987]对这个关键问题提供了指导。划分聚类算法经常通过最优化基于全局(在所有的模式上)或局部(模式的一个子集)的准则函数来产生聚类结果。对可能标记集的组合搜索得到最佳准则很明显计算代价太大。因此,在实践中,这个算法典型的运行关联的次数以不同的开始状态,并且从所有的运行中获得最好配置被运用在输出聚类中。
5.2.1. 方差算法
在划分聚类中最直观和最常用的目标函数方法是方差准则,这在单独的和紧凑的聚类中表现良好。一个模式集X(包含K聚类)的聚类L的方差方法是:
\[\large e^2\left (\mathcal{X},\mathbf{L} \right )=\sum_{j=1}^{K} \sum_{i=1}^{n_j}\left \| \mathbf{x}_i^{(j)} -\mathbf{c}_j\right \|^2 \]
其中$\large \mathbf{x}_i^{(j)} $是第i个模式属于第j个聚类并且cj是第j个聚类的中心。
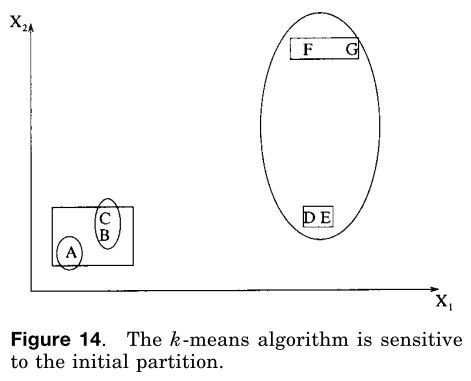
k-means算法是最简单和最常用的应用方差准则[McQueen 1967]的算法。它以一个随机的初始划分作为开始,并且依据两个模式之间的相似度合聚类中心来指派模式属于哪一个聚类集直到某一个收敛准则被满足(例如,不存在任何从一个聚类到另一个聚类的模式再赋值,或者在迭代多次后方差停止明显的减少)。K-means算法之所以流行是因为它很容被实施并且它的时间复杂度为O(n),其中n为模式的数量。K-means算法的一个主要问题是它对初始划分敏感,并且如果初始划分不合适,则可能会集中于准则函数的局部最小值。图14展示了七个二维模式。如果我们一开始以A、B、C三个模式作为构造三个数据集的初始的方法,紧接着,我们以如图椭圆所示的{{A}、{B,C}、{D,E,F,G,}}作为划分结果。这种划分的方差准则值远比如长方形所示的最佳划分{{A,B,C}、{D,E}、{F,G}}的大,最佳划分对于一个包含三个子集的聚类产生一个基于方差准则的最小值。正确的划分为三个子类的解决方案是通过选择得到的,例如,A、D和F作为初始聚类方法。
方差聚类方法
(1)选择一个具有既定聚类数目和聚类中心的初始划分。
(2)分派每一个模式到离他最近的数据中心的类中并计算新的数据中心作为新类的数据中心。重复这一步骤指导聚集被获得,也就是说,直到所有的聚类成员都是稳定的。
(3)基于一个启发信息来合并和分裂聚类,有选择的重复第(2)步。
k-Means聚类算法
(1)选择与K个随机选择的模式一致的K个数据中心或者在包含模式集的超体积的K个随机定义的点。
(2)分派每一个模式到聚类中心离它最近的聚类当中。
(3)用当前的聚类成员重新计算聚类中心。
(4)如果收敛判定准则没有满足,则重复第(2)步。典型的收敛判定准则是:没有(或最低)模式指派到新的聚类中心,或者方差没有减少。
K-means算法的几个变异算法[Anderberg 1973]已经在文献里被提出。它们中的一些试图选择一个好的初始划分以至于算法更可能找到全局最小值。
另一个变异是允许分割和合并生成的聚类结果。有代表性的是当一个聚类的方差大于预先定义的阈值时,它需要被划分,当两个聚类中心距离小于另一个预先的阈值时,它们需要合并。运用这个变异,从任何初始划分中得到最佳聚类是可能的,前提是指定的阈值要合理。
著名的ISO-DATA算法[Ball和Hall 1965]使用了这种合并和划分聚类的技术。如果图14所示的椭圆划分作为ISODATA的初始划分,它将产生最优的三个聚类划分。ISODATA将会首先合并{A}和{B,C}到一个聚类当中因为他们的中心距离很小。紧接着因为存在着大的方差,所以{D,E,F,G}类会被分割成两个类{D,E}和{F,G}。
图14 k-means算法易受初始划分的影响
K-means算法的另一个变异是涉及选择一个完全不同的准则函数。动态聚类算法(允许除了中心之外的代表)被提出来在Diday[1973]和Symon[1977]并且描述了一个动态的聚类方法,这个方法是在系统阐释最大似然函数框架中得到的。正规化的马氏距离被用在Mao和Jain[1996]来获得层次化聚类。
5.2.2. 图论聚类
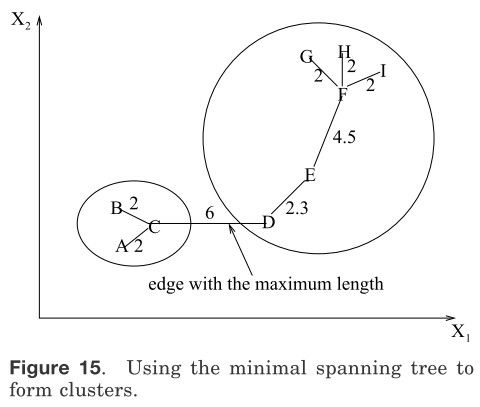
最著名的图论划分聚类算法是基于数据的最小生成树(MST)[Zahn 1971]并且用最大的距离探测MST的边缘。图15表明MST是从9个二维点获得。通过用一段6单位来破坏标签C、D之间的连接(边缘具有最大的欧氏距离),得到两个聚类{A.B.C}和{,D,E,F,G,H,I}。第二个类可以继续划分为两个聚类通过分裂边缘距离为4.5单位的EF。
图15 使用最小生成树生成聚簇
层次聚类和图论算法是有联系的。单链接聚类是数据最小生成树[Gower 和 Ross 1969]的子图也是联通分量[Gotlieb和 Kumar 1968]。全链接聚类是最大完整子图并且和图节点的着色性有关[Backer 和 Hubert 1976]。在Augustson 、Minker[1970]和Raghavan 、Yu[1981]看来最大完全子图被认为是聚类最严格的定义。对于一个没有层次结构和重叠的聚类图驱动的方式在Ozawa[1985]中有表现。通过连接泰森多边形法的所有邻接点对得到德劳内图(DG)。DG包含所有的在MST中包含的所有信息和关联的邻接图(RNG)[Toussaint 1980]。
5.3. 混合分析和模式探索方法
聚类分析的混合分析算法已经考虑到很多方式。基础的假定是将要聚类的模式是从几个分派中获得并且目标是识别出每一个的参数和(也许)它们的数量。这一部分的大部分的工作已经假定混合密度的独立组件是高斯分布的并且在这种情况下每个独立的高斯的参数将通过程序来估计。对于这个问题的传统方法涉及到得到(迭代的)这些元件密度参数[Jain 和 Dubes 1988]向量的最大似然估计。
最近,期望(EM)最大化算法(一个通用的解决遗漏数据问题的最大似然估计算法)已经被用在了参数估计的问题上。一本近期的书[Mitchell 1997]对于这种技术提出了一种可接受的描述。在EM框架中,像混合参数一样,元件密度参数是未知的并且从模式中有估计。EM程序以一个参数向量的初始估计开始并且迭代的通过参数向量产生的混合密度来修复模式。被修复的模式将被用来更新参数状态。在一个聚类文本中。大量的模式(本质上测量把它们从混合的单一组件中提取出来的可能性)可以被看做模式类的暗示。这些放在一个特殊组件中模式将被看成是属于相同的聚类。
对于密度聚类算法的非参数技术也已经被开发出来[Jain 和 Dubes 1988]。受到非参数密度估计的派忍创制方法的启发,相关的聚类程序探索具有大数量频率在输入模式集的混合模式直方图中。其它的方法包括其它划分或层次聚类算法的应用用一个基于无参密度估计的距离度量。
5.4. 最邻近聚类
因为在我们的直观感觉里紧邻扮演着关键角色,最近对距离可以作为聚类程序的基础。Lu和Fu[1978]提出了一种迭代处理过程,它是把每一个没有标注的模式分派到离它最近的聚类中,前提是它到标签邻居的最近距离小于某一个阈值。持续以上处理直到所有的模式都被标注或没有添加标签发生。相互邻接距离(在先前的距离计算中有描述)可以被用来从相邻类中生成聚类。
5.5. 模糊聚类
传统的聚类方法形成划分;在每一个划分里,每一个模式仅属于一个聚类。因此,在一个硬聚类中类与类之间是不相交的。模糊聚类扩展了这个概念用成员函数[Zadeh 1965]来联系每一个模式和所有聚类。这些算法的输出时一个聚类但不是一个划分。我们在下面给出了一个高级的划分模糊聚类算法:
模糊聚类算法
(1)选择一个初始模糊划分,划分通过选择N×K的成员矩阵U把N个实体分配到K个聚类当中。这个矩阵中的一个元素uij表示成员xi在聚类cj的可能性。典型的,uij[0,1]
(2)利用U找到模糊准则函数的值,例如一个加权的平方差准则函数,来联系关联划分。一个可能的准则函数是
\[\large E^2\left ( \mathcal{X},\mathbf{U} \right )=\sum_{i=1}^{N}\sum_{k=1}^{K} u_{ij}\left \| \mathbf{x}_i-\mathbf{c}_k \right \|^2\]
,其中$\large \mathbf{c}_k=\sum_{i=1}^{N} u_{ik}\mathbf{x}_i$ 是第k个模糊聚类的中心。
再分配模式到聚类当中来减少这个准则函数的值并重新计算U。
(3)重复第二步直到进入U不再很大程度的改变。
图16 模糊聚簇
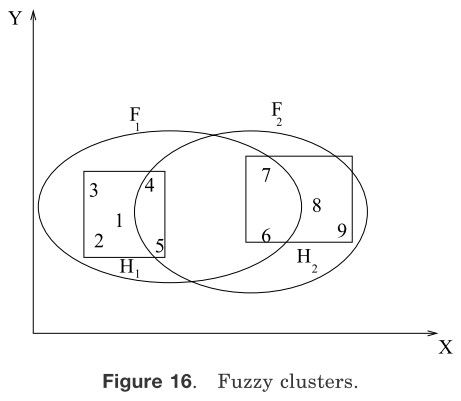
在模糊聚类当中,每一个类对于所有的模式都是一个模糊的集合。图16阐释了这个观点。长方形围绕数据的两个硬聚类:H1={1,2,3,4,5}和H2={6,7,8,9}。一个模糊聚类算法可能会产生两个模糊由椭圆描述的聚类F1和F2。模式将有对于每一个类的属于[0,1]的隶属度值。例如,模糊聚类F1可以被简单地描述如下:
{(1,0.9),(2,0.8),(3,0.0),(4,0.1),(5,0.55),(6,0.2),(7,0.2),(8,0.0),(9,0.0)}
F2可以被描述如下:
{(1,0.0),(2,0.0),(3,0.0),(4,0.1),(5,0.15),(6,0.4),(7,0.35),(8,1.0),(9,0.9)}
有序对(i,ui)在每一个聚类中表示第i个模式和它与模式ui的关联权值。较大的隶属度表示模式分配到该聚类的较高的置信度。一个模糊聚类可以通过隶属度阈值转换得到硬聚类。
模糊数据集理论最初被Ruspini[1969]应用在聚类中。Bezdek[1981]著的书是关于模糊聚类很好的资源。最为流行的模糊聚类算的是模糊c-means(FCM)算法。尽管在避免局部极值方面它要比硬聚类K-means算法要好,但是它仍会聚集于方差的局部极值。联系函数的设计是模糊聚类最重要的问题;不同的选择包括基于相似分解和型心的聚类。FCM的一般性算法是Bezdek[1981]通过一个目标函数族来提出的。一个c-shell算法和一个适应探测圆和椭圆边界的变异算法被Dave[1992]提出来。
5.6. 表征聚类
在一个应用当中,类的数目或数据集的聚类被发现,数据的划分是最终结果。此时,一个划分给出了一个数据点到类的可分性思路并且怀疑假定在数据集上给定类的数目的有监督分类是否有意义的。然而,在涉及决策的很多应用中,结果聚类不得不被以一个紧凑的方式表现或描绘来获得数据抽象。尽管一个聚类表现的结构在决策机制中是重要的一步,但是它并没有被研究者紧密的检查。聚类表示的概念被Duran和Odell[1974]提出来并且随后被Diday、Simon[1976]和Michalski[1981]等加以研究。他们提出以下表示机制:
(1)通过它们的图心或聚类中一些远距离点的集合代表一个聚类。图17表现了这两种思路。
(2)运用分类树中的节点代表聚类。如图18所示。
(3)通过连接的逻辑表达式来表示聚类。例如,图18中表达式[X1 >3][X2 <2]表示X1的逻辑状态大于3并且X2的逻辑状态小于2
图17 使用点代表聚簇
图18 使用连接陈述或分类树来代表聚簇
利用图心来代表一个聚类是最常用的机制。当聚类是紧凑或各向同性时这种机制效果良好。然而,当聚类是松散的或不是各向异性的时候这种机制就不能很好的表现。在这样的情况下,运用采集聚类边界点的方法能很好的捕获它的外观。用来表示聚类的边界点的数目随着形状的复杂度的增加而增加。这两种描述在图18中被等价表示了出来。在分类树中,从根节点到叶子节点的每一条路径与连接词状态相符。简单连接词表示概念的一个重要的限制是它们只能够描述特征空间是矩形或各向同性聚类。
数据抽象之所以有用是由于一下原因:
(1)它提供一个让人们易于理解的简单和直观的聚类描述。在概念聚类[Michalshi和Stepp 1983]和符号聚类[Gowda 和 Diday 1992]着种描述都不需要用附加的步骤来得到。这些算法既生成聚类也生成它们的描述。一个模糊规则的集合能够从数据集中的模糊聚类来得到。这些规则能够被用来建立模糊分类器和模糊控制器。
(2)它帮助获得能够更用电脑进一步开发的数据压缩[Murty 和 Krishna 1980]。图19显示了标签为1和2的两个链装聚类。像K-means算法一样的划分聚类算法不能够很好的划分这两个结构。单连接算法在这个数据集上表现良好,但是运算复杂度太高。所以一个混合方法可以用来开发这些算法共同的属性。用K-means(高效运算)算法我们得到了8 个子聚类。如图19(a)所示,每个聚类都可以被它们的中心来代表。现在单链接算法可以单独被应用与它们得到两组。结果组在图19(b)中显示。在这里,数据简化是通过中心表示子聚类来表示的。
图19 使用聚类压缩
(3)它增加了决策的效率。在一个基于聚类的文档检索技术[Salton 1991]中,大量的文档被聚类并且每一个聚类结果都是用中心来表示。检索文档需要相关的查询,查询是与聚类中心相比较而不是和所有的文档。这能高效的检索相关文档。在涉及到大量数据集的几个应用当中,聚类是用索引来表现,而这能够帮助高效率的检索[Dorai和Jain 1995]。
5.7. 人工神经网络聚类
人工神经网络(ANNs)[Hertz et al 1991]是由生物神经网络产生的。人工神经网络在过去30十年已经被广泛的应用在分类和聚类[Sethi 和 jain 1991;Jain 和 Mao 1994]中。ANNs在模式聚类中很重要的一些特征是:
(1)ANNs处理数值向量,所以这要求模式只能用数值特征来表现。
(2)ANNs是内在关联的和分布式处理架构。
(3)ANNs可以学习它们的权值进行自适应[Jain 和 Mao 1996;Oja 1982]。更专业的来说,通过适当的选择权值,它们能够进行模式标准化和特征选取。
竞争(胜利者优先)神经网络经常被用来聚类输入数据。在竞争性学习中,相似的模式被分为一组并且用一个单独的单位(神经元)表示。这个分组过程是依据数据相关自动完成的。用来聚类的ANNs的著名的例子包括神经网络学习向量量化(LVQ)和自组织映射(SOM)[Kohonen 1984]以及自适应谐振理论模型[Carpenter 和 Grossberg 1990]。这些ANNs的结构很简单:它们都是单层的。模式再输入时加入并且在输出节点相联系。输入节点之间或输出节点之间的权值是不断变化(这被称为学习)的直到一个结束标准被满足。竞争性学习已近被发现存在于生物神经网络。然而,学习或权值更新程序和那些经典聚类过程相当相似。例如,K-means和LVQ之间的联系Pal et al[1993]有阐释。在ART模型中的学习算法和领导者聚类算法相似[Moor 1988]。
SOM对于多维数据集给出了一个直观上吸引人的二维映射,并且它已经被应用在矢量分层和语音识别[Kohonen 1984]。然而,就像连续的副本,在初始分组没有被合适的选择的情况下,SOM产生一个次优的划分。更有甚者,它的收敛控制是通过各种参数如学习速率和一个邻居节点的胜利而发生的。对于一个特定的输入模式,通过不同的迭代次数产生不同的输出单元是可能的;这就产生了学习系统的稳定性问题。在有限的学习迭代之后训练数据集中没有模式改变它的所属类别时,它就被认为是稳定的。这个问题是和可塑性紧密相连的,可塑性就是算法适应新的数据集的能力。为了稳定性,当迭代过程和这影响到可塑性时,学习率应该被减至零。ART模型被认为是稳定和可塑性的[Carpenter 和Grossberg 1990]。然而,ART网是依赖有序的;也就是说,网中数据展现的不同数据顺序导致不同的划分。同时,从ART网中产生的聚类的规模和数量依赖于选择的警戒阈值,警戒阈值被用来决定一个模式是否属于一个已经存在的聚类中或者开始一个新的聚类。更进一步,SOM和ART适用于探测超球面聚类[Hertz 等 1991]。在两层的网络中运用正规化的马氏距离来提取超球面聚类被Mao和Jain[1994]提出来。所有这些ANNs都运用固定数目的输出节点来限制可能产生的聚类数量。
5.8. 用于聚类的进化算法
进化算法的灵感来自于自然界的进化演变,利用进化运算子和众多解来获取数据的全局最优划分。聚类问题的候选解被编码为染色体。最常用的进化运算子是选择,重组和突变。每次输入一个或多个染色体,经过转换,输出一个或多个染色体。适应函数会评价染色体下次迭代中幸存的概率。我们给出一个应用于聚类的进化算法的抽象描述如下:
用于聚类的进化算法
(1) 随机选择一组解,每个解对数据集的一个合法的k划分。然后为每个解设置一个适应值。一般来说,适应值与方差成反比,所以一个方差较小的解的适应值也较大。
(2) 使用进化算子(选择、重组和突变)生成下一代解。计算这些解的适应值。
(3) 重复步骤2直到满足停止条件
著名的进化算法有遗传算法(GAs)[Holland 1975; Goldberg 1989],进化策略(ESs)[Schwefel 1981]和进化规划(EP)[Fogel et al. 1965]。这三种算法中,最常在聚类应用的算法是GAs。GAs的解一般为二进制字符串。在GAs的步骤中,选择算子根据解的适应性将解从当前这一代繁衍到下一代。选择算子是以一种概率方法进行的,具有高适应性的解其生殖的可能性越高。
图20 交叉操作
重组的方法有很多,其中交叉是最常用的。如图20所示,交叉是一对染色体(父母)转化为另一对新染色体(孩子或后代)。图20显示的是一个单点交叉运算,它将父母染色体中超过交叉点的片段进行了交换。例如,父母染色体为二进制字符串“10110101”和“11001110”。交换父母染色体在交叉点(从左数的第四位和第五位之间)之后的片段,这样就产生了孩子染色体。突变运算子是将一个染色体上任意一位置上比特值取反。例如,将突变运算应用于字符串“10111110”,对其(从左数)第二位比特取反,就得到了字符串“11111110”。交叉和重组都是根据染色体的适应性,以某一预设的概率作用于染色体上的。
GAs以二进制字符串来表示点,并依靠交叉算子来搜索点空间,使得点空间的所有部分都不会被遗漏。在解的表现形式和交叉算子的类型上,ESs和EP与GAs不同。EP没有重组算子,只有选择和交叉算子。当用以聚类问题时,这三种算法用以减小方差。Fogel和Fogel[1994]研究了这些算法的理论问题,诸如收敛性等。
\[\large \begin{matrix}
01!000\\
11!111 & \\
\end{matrix}\]
GAs是全局搜索,但大多数其它聚类方法是局部搜索。在局部搜索中,下一次迭代的解是在当前迭代的解的附近。从这个意义上讲,k-means算法,模糊聚类算法,ANNs,各种不同的退火方法(如下所述)和tabu搜索都是局部搜索技术。而GAs通过交叉和突变运算子可以产生与当前解完全不同的新解。如图21所示。假设标量X由5比特表示,S1和S2代表一维空间中的两点,其值为8和31,相应的它们的二进制数分别为01000和11111。我们将交叉点设置在第二位和第三位之间,并执行交叉运算。
交叉运算将产生新染色体:S3=01111和S4=11000,对应的十进制数为15和24。类似地,通过使二进制字符串01111(十进制值15)的最高位发生突变,就生成了二进制字符串11111(二进制值31)。
最早将GAs应用于聚类的论文大概是Raghavan和Birchand[1979],在这篇论文里,GA用于最小化聚类的方差。这里,我们将每个点或染色体用长度为N的K进制字符串代表。例如,假设有6个模式——A,B,C,D,E和F和字符串101001。这个6比特二进制(K=2)字符串表示将6个模式放入两个聚簇中,其中第一个,第三个和第六个模式放入一个聚簇,第二个聚簇拥有剩下的模式。也就是说,这两个聚簇是{A,C,F}和{B,D,E}(6比特二进制字符串010110代表的就是这个意思)。当有K个聚簇时,就会有K!个不同的数据集的K划分,也就是有K!个染色体。这样,有效的搜索空间就以K!倍数增加。此外,两个较好的染色体交叉后,其后代可能较差。
例如,上述6个模式的一种聚簇为{A,B,C}和{D,E,F},对应的染色体为111000和000111。通过交叉这两个字符串第三个之后的片段,我们得到111111和000000。而这两个后代对应的划分较差。这些问题促使研究者们设计更好的表现形式和交叉算子。
Bhuyan等人[1991]提出了一种改进的表现形式,即使用一种额外的分割符(*)和模式标志来代表某一划分。染色休ACF*BDE代表两个划分{A,C,F}和{B,D,E}。使用这一表现形式使得它们可以将聚类映射到排列组合问题,而诸如旅行商问题这样的麻烦可以使用排列组合交叉算子解决[Goldberg 1989]。但这一解决方法会遇到排列冗余的困难。例如,划分{A,C,F}和{B,D,E}就有72个等价的染色体。
最近,Jones和Beltramo[1991]研究了如何将边界交叉[Wihitley et al. 1989]用于聚类。他们假设将聚簇中的所有模式相互连接成一个完全图。父母模式产生的后代继承了从其父母出发的边。研究观察到这种交叉算子需要Ο(K6+N)的时间将N个模式聚集成K个聚簇,而且当聚簇超过10个时,其对实际数据集就没有通用性了。Babu和Murty[1993]提出了一种混合方法,他们只将GA用于寻找好的初始聚簇中心,而使用k-means算法寻找最终聚簇。这种混合方法要比单纯的GA好。
GAs的最大问题在他们易受诸如数据集大小,交叉和突变概率等各种参数的影响。Grefenstette[Grefenstette 1986]研究了这个问题,并提出了选择这些控制参数的准则。但是在诸如模式聚类这样的特殊问题上,这些准则不一定会产生好结果。Jones和Beltramo[1991]的研究表明,特殊问题启发式的混合遗传算法擅长聚类。Davis[1991]研究了GAs在其它实际问题中的应用,得出与Jones和Beltramo相似的结论。GAs的另一个问题是选择一个适当表现形式,这一表现形式的规则要少,定义的长度要短。
我们可以将聚类看成最优化问题,直接找出聚簇的最优质心,而不是使用GA寻找最优划分。这一想法使ESs和EP变得可用,因为这些算法支持实数向量解的直接表示,能很容易对质心进行编码。Babu和Murty[1994]将ESs用于硬和模糊聚类问题。EP已经用于产生模糊最小最大聚簇[Fogel and Simpson 1993],结果表明聚类效果比传统的k-means算法和模糊c-means算法要好。但是,与GAs和ANNs类似,这些算法也都易受控制参数的影响。所以人们不得不专门为每一个问题调谐参数值。
5.9. 基于搜索的技术
用以获得判别函数的最优值的搜索方法分为确定性搜索方法和随机性搜索方法。确定性搜索方法通过穷举法来产生最优分割,而随机性搜索方法可以快速地生成近似最优分割,并能确保逐渐接近最优分割。至此,我们讲的所有算法中,进化算法是随机性,其它算法都是确定性的。它用聚类的确定性方法还包括Koontz等人[1975]和Cheng[1995]采用的分枝定界法,这一方法需要大量的计算才能生成最优分割。Rose等人[1993]提出一种用以聚类的确定性退火算法,这一算法采用了一种误判面平滑的退火技术,但不能保证收敛到全局最优。Hofmann和Buhmann[1997]研究了使用确定性退火的接近模式的聚类(模式是以成对指定而不是多维点);他们接着又将确定性退火技术应用于文本分割[Hofmann and Buhmann 1998]上。
确定性方法是典型的贪婪下降方法,而随机性方法允许以非零的概率在非局部最优方向上趋近于解。随机性方法不是串行的,就是并行的,但是进化算法的本质就是并行。模拟退火算法(SA)[Kirkpatrick et al. 1983]是一种串行随机搜索算法,Klein和Dubes[1989]讨论了其在聚类中的应用。模拟退火算法通过以某些概率来接受新解使得下一迭代较差(通过判别函数度量),避免(或从中恢复)陷入使用目标函数局部最优的解。接受新解的概率由判别参数——温度(与现实中的退火类似)决定,温度通常由初始温度(第一次迭代)和最终温度决定。Selim和Al-Sultan[1991]研究了控制参数对算法性能的影响。Baeza-Yates[1992]使用SA获取数据集的近似最优解。SA从统计学上保证找到全局最优解[Aarts and Korst 1989]。基于SA的聚类算法的抽象步骤如下:
基于退火算法的聚类
(1) 随机选择一个初始划分P0,并计算其方差Epo。为控制参数(初始温度T0和最终温度Tf);
(2) 选择P0的一个邻居P1并计算其方差Ep1。如果Ep1比Ep0大,那么将P1中的元素以与温度有关的概率分配给P0,否则将P0分配给P1。按预先设置的次数重复此步骤;
(3) 减小T0,比如T0=cT0,其中c是预先设置的常量。如果T0比Tf大,跳至第2步,否则停止。
由于每次迭代搜索最优值时温度必须下降得很慢,所以SA算法可能会比较慢。
与SA类似,Tabu搜索[Glover 1986]是一种跳出可行性边界或局部最优,系统地允许和约束对其它禁止区域进行搜索的算法。Al-Sultan[1995]里就将Tabu搜索用于聚类问题。
5.10. 聚类技术对比
在这一节里,我们将像解最优化问题那样,使用各种确定性和随机性搜索技术来解决聚类问题。这些技术中大部分使用方差判别函数。所以,它们生成的分块并不像层次算法那样通用。进化算法是全局性搜索技术,而其它方法则是局部搜索技术。ANNs和GAs的本质是并行的,所以它们可以使用并行硬件来加速。进化算法是基于群的;也就是说,这些方法一次使用多种解来搜索,而其它方法一次只能使用一种解。ANNs,GAs和SA和Tabu搜索(TS)都易受到学习参数或控制参数的影响。从理论上看,由于这四种方法都没有使用明确的领域知识,所以它们都是弱方法[Rich 1983]。评价方法的一个重要特征在于它能找到最优值,即使判别函数是离散的。
Mishra和Raghavan[1994]对启发式方法的聚类效果进行了实验研究;评价了SA,GA,TS,随机化分枝定界(RBA)[Mishra and Raghavan 1994],混合搜索(HS)策略[Ismail and Kamel 1989]。结果表明:一维数据情况下GA表现较好,但是GA在高维数据集上的表现较差;SA由于太慢而不引人注意;RBA和TS表现最好;HS擅长处理高维数据;没有一种方法远胜于其它方法。Al-Sultan和Khan[1996]对k-means,SA,TS和GA进行了实验研究,结果表明:TS,GA和SA在解的质量上可圈可点,而且都比k-means方法好。但是k-means的执行时间更短;其它方法则需要更多的时间(倍数为500到2500)来将大小为60的数据集分割为5个聚簇。此外,在产生最好解的速度方面GA快于TS和SA,SA的速度最慢。但是GA聚类的时间最长,也就是获得最佳解的时间最长,TS和SA的效果则相对较差。值得注意的是Mishra和Raghavan[1994]与Al-Sultan和Khan[1996]进行实验的数据集都较小,都没少于200个模式。
Mao和Jain[1996]使用了一种二层网络。第一层网络包括一些主要部件分析子网,第二层网络使用竞争网络。这一网络通过正规化的马氏距离来进行分割式聚类。先使用1000个从大图像中随机选择的像素点来训练网络,然后用心对图像中的每个像素点进行分类。Babu等人[1997]提出一种随机连接方法(SCA),并在标准数据上与SA和k-means进行性能比较。结果表明SCA在解的质量上高于SA和k-means。但只有当数据为低维数据且其数量小于1000时,评价指标才算是好的。
总之,只有k-means算法及其ANN等价算法——Kohonen网[Mao and Jain 1996]已经被应用于大数据集处理中;其它算法已经处在测试阶段,但一般来说,还是在小数据集上试验。这是因为ANNs,GAs,TS和SA的学习参数和控制参数很难获取,而且这些算法在大数据集上的执行时间太长了。[Selim and Ismail 1984]显示k-means方法会收敛到局部最优解,这与k-means算法在初始种子上的选择有关。所以如果能使用其它方法快速地得到一个好的初始划分,那么即使是在大数据集上,k-means也能很好地进行聚类。尽管本节讨论的各种方法效果相对较差,但经验表明,领域知识可以帮助改善性能。例如,进行图像分类时,ANNs使用从原始图像提取的特征进行聚类的效果比直接使用原始图像更好。同样的,混合分类器比ANNs[Mohiuddin and Mao 1994]。类似地,将领域知识加入GA可以改善其性能[Jones and Beltramo 1991]。所以使用领域知识可以提高诸如GA,SA,ANN和TS这类算法的性能。但是这类算法(具体就是算法的判别函数)倾向于生成超球面的聚簇分块。例如,[Rasmussen 1992]的研究表明在基于聚类的文档检索中,层次算法表现得要比划分算法好。
5.11. 聚类的域约束
聚类作为一个任务带有主观性质。为了不同的目的,可能需要对相同的数据进行不同的划分。例如这样的数据,一条鲸鱼,一只大象和一条金枪鱼[Watanabe 1985]。鲸鱼和大象组成哺乳动物的聚簇。但是,如果用户对水中生物感兴趣的话,那么鲸鱼和金枪鱼就会被聚合在一起。一般来说,通过将领域知识加入到聚类的一个或多个过程中,可以将这种主观观念加入到聚类判断标准中。
每一种聚类算法都明着暗着使用了某些知识。“暗着”的知识能起到如下作用:(1)选择一种模式代表方法(例如使用一个人的过去的经历来选择特征和对特征进行编码);(2)选择一种相似度度量方法(例如,使用马氏距离来获得超椭圆体的聚簇,而不是欧氏距离);(3)选择一组方法(例如如果预先得知聚簇是超球面的,使用k-means算法)。“暗着”使用领域知识的算法有ANNs,GAs,TA和SA,它们使用领域知识用心寻找使用算法性能最好的控制参数或学习参数。
我们同样可以使用明确可用的领域知识来限制或指导聚类过程。这种专门的聚类算法已经被某些应用系统所使用。领域概念可以在聚类过程中发挥不同的作用,所以从业者可以有多种不同的选择。一个极端的例子是可用的领域概念能简单地作为额外的特征加入聚类,但聚类过程的其他部分却不受影响。另一方面,领域概念可能被用于证实或否定传统聚类算法独立作出的决策,或者被用于通过近似来影响聚类算法中距离的计算。领域知识的加入主要由专业但共同点少的算法构成,相应地,我们对想法的讨论将主要由动机和过去工作的简要调查构成。这一领域是机器学习和模式识别的交叉领域,感兴趣的读者可以进一步阅读机器学习领域的著名期刊(如Machine Learning,Journal of AI Reserach或者Artifical Inteligence)。
如Cheng和Fu[1985]所提,专家系统的规则可能会被聚集以减少知识数据库的大小。聚类上的这一改变也被Lebowitz[1987]应用在大学,国会投票记录和恐怖事件上。
5.11.1. 相似度计算
在Michalski和Stepp[1983]里概念知识已经被明确地应用于相似度计算阶段。它是基于这些假设,即有模式表现且使用动态聚类算法[Diday 1973]来对模式进行分组。组成的聚簇使用连接的陈述的谓词逻辑表达。Michalski和Stepp[1983]和[1986]提到,使用概念聚类得到的分组比使用数值方式要好。Dale[1985]鉴定分析了这些工作,它观测到单元划分聚类算法可以生成使用连接的陈述描述的聚簇。例如在图8里,使用单元算法获得的四个聚簇可以使用连接的概念进行陈述,如下所示:
\[\large \begin{matrix}
Cluster1:\left[\mathbf{X} \leqslant a \right] \wedge \left[\mathbf{Y} \leqslant b \right] \\
Cluster2:\left[\mathbf{X} \leqslant a \right] \wedge \left[\mathbf{Y} > b \right] \\
Cluster3:\left[\mathbf{X} > a \right] \wedge \left[\mathbf{Y} > b \right] \\
Cluster4:\left[\mathbf{X} > a \right] \wedge \left[\mathbf{Y} \leqslant b \right]
\end{matrix}\\
\]
其中^是布尔连接操作符“和”,a,b和c是常量。
5.11.2. 模式表示
Srivastava和Murty[1990]表明,与数值分类方法类似,模式表示阶段隐式地使用知识,可以生成与概念聚类相同的划分。在这个意义上,概念聚类和数值分类就是等价的,而不是完全对立的。概念聚类显式地使用领域知识来计算内模式的相似度计算,而数值分类则隐式地假设模式表现由领域知识获得。
5.11.3. 聚簇描述
一般来说,在基于知识的聚类过程中,会生成聚簇及其说明或特征[Fisher and Langley 1985]。但也有例外,比如Gowda和Diday[1992]就只生成了聚簇,但没有显式地生成任何聚簇描述。在概念聚类中,事物的一个聚簇是由连接起来的逻辑表达式表达的[Michalski and Stepp 1983]。尽管连接陈述是人类最常用的描述形式,但它是受限制的。Shkar等人[1987]使用事物的功用性知识生成更加直观且吸引人的聚簇描述,这些聚簇描述使用布尔隐式操作符。Fisher[1987]提出了一种显示聚簇概率的系统;这些描述比连接概念更加通用,而且非常适合层次化分类领域(比如动物物种层次)。Fisher和Langley[1985]第一个完成了概念聚类系统,产生的聚簇使用概率进行描述。Murty和Jain[1995]也提出了一个类似的聚类模式,但其使用所有连接和非连接的逻辑表达式进行描述。
如果聚类过程会产生连接概念,那概念聚类可以将以定性或定量的特征描述的事物进行分组,这是概念聚类的一个重要特征。例如板球,
\[\large \begin{align*}
color = red&\wedge \left ( shape=sphere \right ) \\
&\wedge (make=leather)\\
&\wedge (radius=1.4inches)
\end{align*}\]
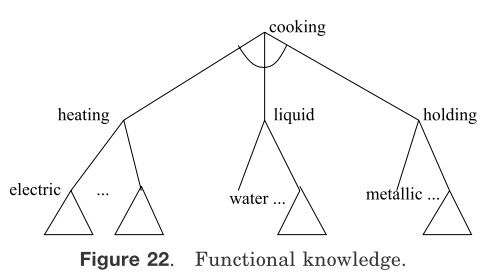
这个概念以半径作为其定量描述,其它板球特征则是定性特征,这些可以用来描述板球聚簇。Stepp和Michalski[1986]使用一种图(目的依赖网络)来对结构化事物进行分组。Shekar等人[1987]使用功用性知识来对人工事物进行分组。功能性知识可以使用“和/或”树加以描述[Rich 1983]。例如图22的cooking,cooking可以分解为holding、heating和liquid(将材料放入水中并加热)。每个人工事物都有其主要功用,不然它们为什么要被造出来呢?此外基于其特征,它可能有其它功能。例如,一本书可以被用于阅读,但如果书很重的话,还可被用做镇纸。Sutton[1993]提出使用事物函数构建类属的识别系统。
图22 功用性知识
5.11.4. 实际困难
所有显式地将领域概念加入聚类技术的系统实现都必须解决好以下几个重要的实际困难:
(1) 领域概念的描述,可用性和完整性;
(2) 如何使用知识进行推论
(3) 如何根据动态知识进行调整
在某些领域,完整的知识是明确可用。比如Murty和Jain[1995]使用ACM Computing Reviews分类树就是完整的,明确可用的。但是在某些领域,知识是不完整,而且不是明确可用的。一般来说,机器学习技术被用于自动抽取知识,这是困难且充满挑战性的问题。最常使用的学习方法是从例子中学习[Quinlan 1990]。这是一种用于从不同领域的每个类中的例子中获取知识的归纳学习范式。即使知识是明确可用的,也很难知道其是否是完整健全的。而且,验证从实际数据集中抽取的知识的完整性和健全性是极其困难的,因为这类知识不能以命题逻辑的形式描述。数据和知识是随着时间而不断变化。例如,图书馆里会不断有新书加入,一些旧书则会从书架上拿下。所以图书馆采用的(知识)分类系统也得定期更新。
基于知识的聚类的一个主要问题在于其还没有应用于大数据集或者拥有大数据集的领域。这是因为一般来说,知识聚类所处理的需要分组的事物数量少于1000,知识规则的数量少于100。所以,最困难问题在于使用大规模知识库对在数据挖掘、图像分割和文档检索中的事物进行聚类。
5.12. 大数据集的聚类
在实际应用中,有时候我们需要对数量庞大的模式进行聚类。那么怎样才叫做数量庞大呢?这是随着计算机技术工艺水平的改变而改变,比如内存和处理时间。在19世纪60年代,几千个模式就称得上数量庞大[Ross1968];而现在,应用系统需要对数量百万级的高维模式进行聚类。例如,为了分割一个长宽500×500的图像,需要对250,000个像素进行聚类。在文档检索和信息过滤领域中,为了完成数据抽象,需要对数百万个维度超过100的模式进行聚类。然而科学文献中提到的大多数方法和算法都无法处理如此庞大的数据集。最优化方法如遗传算法、Tabu搜索和模拟退火受限于适当小的数据集。概念聚类的实现可以优化某些基准函数,但通常其计算代价高昂。
收敛的k-means算法和其ANN等价物——神经网络已经应用于大数据集的聚类[Mao and Jain 1996]。k-means算法的通用性在于以下几点
(1) k-means的时间复杂度为Ο(nkl),其中n为模式的数量,k为聚簇数,l为算法收敛需要的迭代次数。一般来说,k和l是预先设定的,所以k-means具有与数据集大小线性相关的时间复杂度[Day 1992]。
(2) k-means的空间复杂度为Ο(k+n)。它需要额外的空间存储数据矩阵。我们可以将数据矩阵存入一个二级内存,这样就可以按需存取模式。然而由于k-means要反复迭代以收敛,存取时间就多,进而导致处理时间巨量增加。
(3) 它是无规则的,对于一个给定的聚簇中心的初始种子集来说,它会生成的相同划分。这一划分与模式在算法出现的顺序无关。
即使是在最好的情况下,k-means算法的效果也与初始种子的选择有关,它可能只产生超球面的聚簇。
层次聚类算法则更加通用。但是他们都有着如下的缺点:
(1) 层次聚类算法的时间复杂度为Ο(n2logn)[Kurita 1991]。单链接的聚簇可以使用数据的最小生成树获得,二维数据情况下的时间复杂度为О(nlog2n)[Choudhury and Murty 1990]。
(2) 层次聚类算法的空间复杂度为Ο(n2)。这是因为相似度矩阵的大小为n×n。大小为100×100的图像中的所有像素的聚类需要近200M的空间(假设相似度使用单精度存储)。可以按需计算矩阵的元素而不是将它们全部存储起来,但这样会增加算法的运行时间[Anderberg 1973]。
表I 聚类算法的复杂度
表I列出了一些著名算法的时间复杂度和空间复杂度。其中n是被聚类的模式的数量,k是聚簇的数量,l是迭代的次数。
一种对大数据集进行聚类的解决方案应适当少地牺牲聚簇的通用性,以实现更有效的变异的聚类算法。Ross文章中使用了一种混合的方法,像k-means算法一样选择引用点,剩下的数据点被分配到一个或多个引用点或聚簇。为每组点独立地生成最小生成树,合并所有的最小生成树获得全局最小生成树的近似。这种方法的相似度只计算所有点对的一部分,10,000个模式的相似度的数量只相当于2,000个点的所有点对的数量。Bentley和Friedman[1978]提到一种复杂度为Ο(nlogn)的计算近似最小生成树的算法。Zupan[1982]提出一种运行时间以Ο(nlogn)逐渐增加的生成一棵近似系统树图的方法。Venkateswarlu和Raju[1982]提出一种算法加速ISO-DATA。Eddy等人[1994]研究了大数据集的近似单链接聚类分析。
数据挖掘(第6节会作为一个应用系统进行讨论)的兴起驱使大数据集聚类算法的发展。有两个算法不得不提一提,Ng和Han[1994]提出的CLARANS和Zhang等人提出的BIRCH算法。CLARANS(Clustering Large Application based on RANdom Search)通过原数据中重复的随机样本来确定候选聚类矩心。由于随机采样的关系,算法的时间复杂度为Ο(nlogn),其中n为模式的数量。BIRCH(Balanced Iterative Reducing and Clustering)使用动态树来存储候选聚簇的概要信息。这棵分层次地组织在叶节点的聚类。当人为改变聚簇大小的阈值或内存不足时,这棵树将被重新建立。像CLARANS这样的算法的时间复杂度与模式数量线性相关。
以上讨论的在大数据集上工作的算法需要将整个模式集存储在主存里,然而,有些应用系统的主存容量有限,不能将整个数据集存入主存中。对此有三种可能的解决办法:
(1) 模式集可以被存储在二级内存,数据的各个部分可以独立地进行聚类,之后进行合并。这样就不是对整个模式集进行聚类。我将这一方法称为分治法。
(2) 使用递增聚类算法。整个数据矩阵被存储在一个二级缓存中,每次读入一个数据到内存中进行聚类,而且内存中只驻留聚簇的代表以进一步减少空间。
(3) 聚类算法的并行实现。我们接下来用三个小节来讨论这类方法。
5.12.1. 分治法
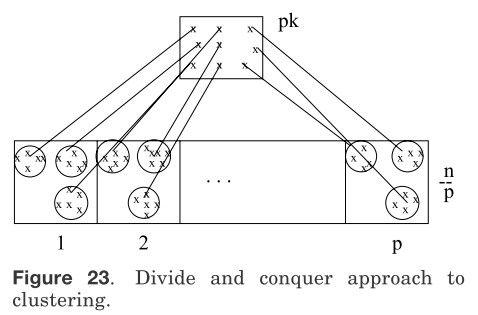
我们将整个n×d模式矩阵存入二级存储空间(比如磁盘文件)。使用[Murty and Krishna 1980]中的聚类算法选择最优的p值,将整个数据分成p块。假设每个数据块中包含n/p个模式。将每个数据块传入主存中并使用标准算法将数据聚类至k个聚簇中,每个聚簇的一个或多个数据代表被单独地存储;这样如果从聚簇中选择一个数据代表,我们就可以得到pk个模式代表。这pk个模式代表可以进一步地被聚类至k个聚簇中,然后这些模式代表所属的聚簇标记用以对原模式矩阵进行重新标记。我们在图23中描述了这一算法的两层结构,这类算法其实可以扩展到任意层次;如果数据集非常大,主存又非常小,那么就需要更高的层次进行聚类[Murty and Krishna 1980]。如表II所示,当使用单链接算法来获得5个聚簇时,聚簇的数量被设置为5,p选取最优值,可以看到计算量有大幅地下降。然而,只有当每个数据块中的数据点都是适当均匀(比如图像)时,这种算法才会运行良好。
表II 双层分治算法法和单链接聚类算法的距离计算次数
Stahl[1986]描述了对2000个模式进行聚类的双层策略。在第一层里,使用领先算法对数据集将聚集成数量巨大的聚簇。通过Ward's的层次方法可以获得每个聚簇的数据代表,并作为第二层聚类的输入。
5.12.2. 增量式聚类
增量式聚类是基于这样的一个假设,即每次只对一个模式进行聚类,其中每次加入聚簇的新数据项不会显著地影响已有聚簇。关于增量式聚类的更深描述如下:
增量式聚类
(1) 置第一个数据对象为聚簇;
(2) 斟酌下一个数据对象。可以置其为新的聚簇,也可以将它加入新的聚簇中。这一步骤需要根据某些判断标准,比如新数据对象与已有聚簇重心的距离;
(3) 重复步骤2,直至所有数据项都已被聚合。
增量式聚类算法的主要优点在于不需要将所有模式矩阵存储到内存中,所以这一算法的空间复杂度非常小。通常他们是非迭代的,所以它们的时间复杂度也非常小。目前的增量式聚类算法列举如下:
(1) 时间复杂度最小的是领导聚类算法[Hartigan 1975],只有Ο(nk)。它因其神经网络的实现——ART网络[Carpenter and Grossberg 1990]而知名。它的空间复杂度仅为Ο(nk)且非常容易实现;
(2) 最短生成路径算法(SSP)[Slagle et al. 1975]起初是用于数据重组,后来被用于自动审计记录[Lee et al. 1978],其中SSP用于对有18个特征的2000个模式进行聚类。这些聚簇被用于估计数据项中丢失的特征值和识别错误的特征值;
(3) cobweb系统[Fisher 1987]也是一种增量式的、概念上的聚类算法。它已经被成功地应用于工程应用系统[Fisher et al. 1993];
(4) Can[1993]提到一种用于动态信息处理的增量式聚类算法。在动态数据库中,数据项每时每刻都在被增加或删除。这便是产生这一算法的动机。这些改变必须反应在生成的分割区内,但不能对现有的聚簇有很大的影响。这一算法被用于对INSPEC数据库中的12.684篇文章进行增量式地聚类。
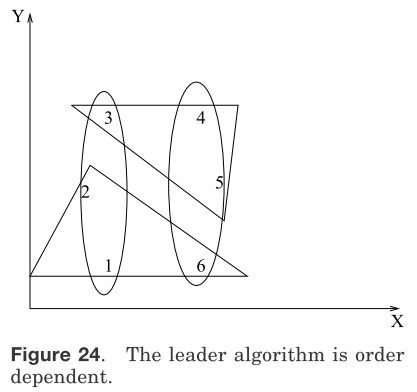
图24 领导算法是次序相关的
聚类算法的一个重要属性就是次序无关性。如果某种算法对于任意次序的数据所产生的分割都是相同的,那么这种算法就是次序无关的,否则就是次序相关的。上述的增量式算法中大多数都是次序有关的,如图24所示。图24中有6个点,分别标记为1,2,3,4,5和6。如果以2,1,3,5,4,6的顺序提供给领导算法进行聚类,所得到的两个聚簇如椭圆形所示。如果以1,2,6,4,5,3的顺序进行聚类的话,所得到的两个聚簇如三角形所示。SSP算法,cobweb和Can[1993]的算法都是次序相关的。
5.12.3. 并行实现
最近,[Judd et al. 1996]表明改进的聚类算法与工作站网络的分布式计算的结合可以使得大小为512×512的图像在数分钟内被聚类完毕。依靠常用的聚类,代码的并行化和提高效率的数据复制可能会使得聚类麻烦不少,然而,一个全局的共享数据结构,即聚簇成员表被保留下来了,它可以被定期地集中管理、复制和同步。在未来,鲁棒且高效的并行聚类技术是决定大规模数据挖掘应用系统的成绩的关键。