Quasi-Newton Method--LBFGS
Quasi-Newton Method
Quasi-Newton Method每一步计算过程中仅涉及到函数值和函数梯度值计算,这样有效避免了Newton Method中涉及到的Hessian矩阵计算问题。于Newton Method不同的是Quasi-Newton Method在每点处构建一个如下的近似模型:
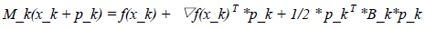
从上面的近似模型我们可以看出,该模型用B_k代替了Newton Method中近似模型中涉及到的Hessian矩阵。因此Quasi-Newton Method中方向计算公式如下所示:
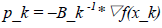 (24)
(24)
这里有必要解释一下用于近似Hessian矩阵的B_k可行性,及一个指导性方案。根据Taylor(泰勒)级数可知如下公式:
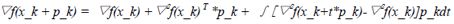
由于函数▽f(.)连续,因此上式可以表示为:
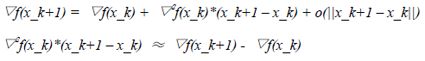
(25)
因此每一选择Hessian矩阵的近似B_ k+1时,可以像式(24)那样模仿真实的Hessian矩阵的性质。得到下式:
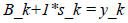 (26)
(26)
其中:
s_k = x_k+1 – x_k y_k = ▽f(x_k+1) – ▽f(x_k) (27)
同时要求B_k+1为对称正定矩阵。
BFGS Method
从Quasi-Newton Method方向公式 (24) 中,可以看到每一步计算方向的过程中均涉及到B_k+1矩阵求逆的问题,为了避免该计算,通过分析公式(26)可知,我们可以构建一个近似H_k+1,该近视满足如下方程:
H_k+1*y_k = s_k (28)
同时要求H_k+1为对称正定矩阵。因此BFGS Method中,每个点处的方向由如下公式计算:
p_k = –H_k*▽f(x_k) (29)
在此基础上,BFGS方向迭代公式如下所示:
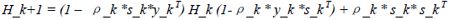
(30)
其中ρ_k为一个标量:
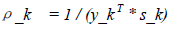
有了上面(30)的H_k迭代公式后,还有一个问题就是初始的H_0如何计算,目前常用的方法是初始的H_0直接设为单位矩阵I。因此BFGS Method用于解无约束最优化的过程可以表示为如下过程:

LBFGS Method
上一节所介绍的BFGS Method比较适合解决中小规模无约束最优化问题,但是BFGS算法产生的Hessian近似矩阵H_k为n * n的,同时该矩阵非稀疏,因此当n的规模较大时将面临两个问题:
1) 存储问题:n规模较大时,n*n矩阵对内存的消耗将较大;
2) 计算问题:n规模较大,同时n*n矩阵非稀疏时,计算复杂度将较高;
为了解决以上问题,引申出了Limited-Memory Quasi-Newton Method,目前使用较多的LBFGS算法即属于该类算法。为了减少H_k矩阵的存储,LBFGS算法利用最近几代的curvature 信息来构建Hessian矩阵的近似。由BFGS Method我们知道:
x_k+1 = x_k + a_k * H_k*▽f(x_k)
其中a_k为步长,H_k为Hessian矩阵的近似,可以通过如下迭代公式计算:
H_k+1 = V_k* H_k*V_k+ρ_k * s_k* s_k (31)
其中:
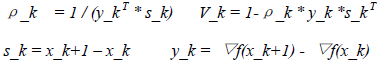
从上面的H_k的迭代计算公式可知,H_k会慢慢由稀疏矩阵转变为稠密矩阵,因此存储该矩阵以及进行该矩阵和向量的相乘运算的消耗将较大。为了避免该问题,LBFGS算法在BFGS算法的基础上从两点进行了改进:
1)估算每一步对应的Hessian近似矩阵时,给出一个当前步的初始Hessian矩阵估计H_k0
2) 利用过去当前代及过去m-1代的curvature信息修正初始Hessian矩阵估计H_k0,得到最终的Hessian矩阵近似估计H_k。
计算式如下所示:
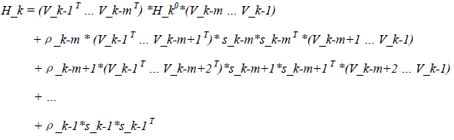
(32)
上述计算式(32),可以通过公式(31)递归计算获取。公式(32)可以用以下算法表示:
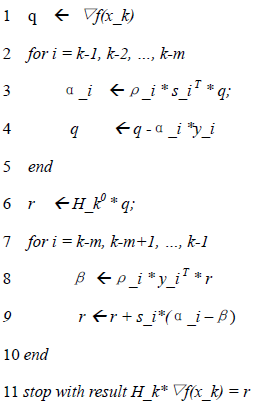
从上面计算H_k的公式(32)可知,要估算每个点x_k处的Hessian矩阵近似,需要给出初始估计H_k0,H_k0一般通过以下公式计算:
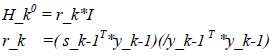
有了上面的方向计算算法后,LBFGS算法用于解无约束最优化问题,可以表示为如下算法:
1 选择一个初始点x_0,并选择收敛判断条件 ε> 0,以及常量m(代表过去代数)一般为6
2 k left 0 H_0 left I,因此r = H_0 *▽f(x_0) =▽f(x_0)
3 while ||▽f(x_k)|| > ε
4 计算从当前点x_k走到下一个点x_k+1的方向
p_k = –r
5 采用line search策略计算步长a_k
6 x_k+1 = x_k + a_k * p_k
7 if k > m
删除LBFGS计算H_k时用不上的向量对(s_k-m, y_k-m)
8 计算并保存 s_k = x_k+1 – x_k y_k = ▽f(x_k+1) – ▽f(x_k)
9 采用LBFGS Hessian矩阵近似算法计算 r
10 k left k+1
4.算法总结
用于解无约束优化算法的Quasi-Newton Method中的LBFGS算法到这里总算初步介绍完了,不过这里笔者要承认的是这篇文档省略了许多内容,包括算法收敛性的证明以及收敛速度证明等许多内容。因此读者若希望对这一块有一个更深入的认识可以参考以下两本书:
1) Numerical Methods for Unconstrained Optimization and Nonlinear Equations(J.E. Dennis Jr. Robert B. Schnabel)
2) Numerical Optimization(Jorge Nocedal Stephen J. Wright)