UESTC 1447 Area 凸包+旋转卡壳 求最大四边形面积

http://acm.uestc.edu.cn/problem.php?pid=1447

给定一组点集，求至多选四点，使其所围成的面积最大。

刚开始四重循环，直接超时掉。后来听说要用到旋转卡壳，且是在求三角形面积基础上求四边形面积的。在AC了一道旋转卡壳法求最大三角形面积后，终于把这道给A了。

本题可以把四边形分为两个三角形的并，再用 旋转卡壳法分别求出这两个三角形的最大面积。

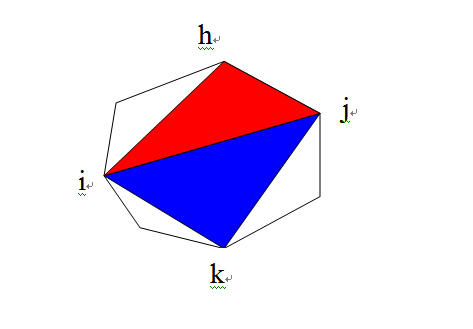
如下图所示，固定i，j点，分别找到这样的h，k点使三角形ijk和三角形ijh面积都最大。

 

#include<stdio.h>

#include<stdlib.h>

#include<string.h>

#include <iostream>

#include <algorithm>

#include<math.h>

using namespace std;

int num,top;

struct Point

{

 int x,y;

 bool operator < (const Point a)const

 {

  return y<a.y||(y==a.y&&x<a.x);

 }

}s[1005],res[1005];

bool multi(Point o,Point a,Point b)

{

 return (b.x-o.x)*(a.y-o.y)>=(a.x-o.x)*(b.y-o.y);

}

int graham(Point s[],int n,Point res[])

{

 sort(s,s+n);

 int len,top=1;

 if(n==0)return 0;

 res[0]=s[0];

 if(n==1)return 1;

 res[1]=s[1];

 if(n==2)return 2;

 res[2]=s[2];

 for(int i=2;i<n;i++)

 {

  while(top&&multi(res[top-1],res[top],s[i]))top--;

  res[++top]=s[i];

 }

 len=top;

 res[++top]=s[n-2];

 for(int i=n-3;i>=0;i--)

 {

  while(top!=len&&multi(res[top-1],res[top],s[i]))top--;

  res[++top]=s[i];

 }

 return top;

}

int Area(Point p1,Point p2,Point p3)

{

    return abs((p1.x*p2.y-p1.y*p2.x)+(p2.x*p3.y-p2.y*p3.x)+(p3.x*p1.y-p3.y*p1.x));

}

int MAX(int a,int b)

{

    if(a>b)

    return a;

    else

    return b;

}

int main()

{

    int aa=1,cas,n,i,j,h,k,top,minx=10005,miny=10005;

    int max1,max2,area,ans,ans1;

    scanf("%d",&cas);

    while(cas--)

    {

    ans=0;minx=10005;miny=10005;

    scanf("%d",&n);

    for(i=0;i<n;i++)

         scanf("%d%d",&s[i].x,&s[i].y);

     top=graham(s,n,res);

     if(top==0||top==1||top==2)

          ans=0;

     else if(top==3)

          ans=Area(res[0],res[1],res[2]);

     else if(top==4)

          ans=Area(res[0],res[1],res[2])+Area(res[0],res[3],res[2]);    

     else

     {

     for(i=0;i<top;i++)

     {

          j=(i+2)%top;

          k=(i+1)%top;

          h=(j+1)%top;

          while(Area(res[i],res[j],res[k+1])>Area(res[i],res[j],res[k]))

               k=(k+1)%top;

          max1=Area(res[i],res[j],res[k]);

          while(Area(res[i],res[j],res[h+1])>Area(res[i],res[j],res[h]))

               h=(h+1)%top;

          max2=Area(res[i],res[j],res[h]);

          ans1=0;

          while(max1+max2>ans1)

          { 

               j=(j+1)%top;

               ans1=max1+max2;

               while(Area(res[i],res[j],res[k+1])>Area(res[i],res[j],res[k]))

                   k=(k+1)%top;

               max1=Area(res[i],res[j],res[k]);

               while(Area(res[i],res[j],res[h+1])>Area(res[i],res[j],res[h]))

                   h=(h+1)%top;               

               max2=Area(res[i],res[j],res[h]);

              

          }

          ans=MAX(ans,ans1);

     }

     }

     printf("Case #%d: %d\n",aa++,ans);

     }

     //system("pause");

     return 0;

}