poj 1328 Radar Installation (简单的贪心)

Radar Installation

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 42925		Accepted: 9485

Description

Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.

We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.

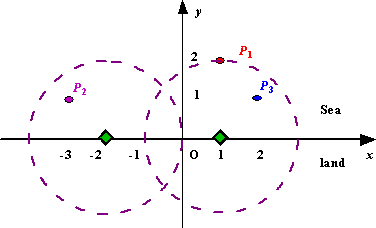
Figure A Sample Input of Radar Installations

Input

The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.

The input is terminated by a line containing pair of zeros

Output

For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.

Sample Input

3 2

1 2

-3 1

2 1



1 2

0 2



0 0

Sample Output

Case 1: 2

Case 2: 1

Source

Beijing 2002

题目链接：http://poj.org/problem?id=1328

题意：有一条直的海岸线，上面有雷达。以海岸线为x轴，x轴上面为海，下面为岸。海里面有很多岛屿。已知雷达的观测半径。问最少建多少个雷达能把所有岛屿都覆盖到雷达

           的侦测范围内。如果不能覆盖全部的岛屿，按样例输出Case数和-1，反之输出Case数和最少需要建立的雷达数。

分析：首先算出经过每个雷达且平行于x轴的弦：假设雷达覆盖半径为d。则弦的左端点为x-sqrt (d*d-y*y),右端点为x+sqrt(d*d-y*y)。然后按左端点从小到大排序。由于不能受右

           端点的影响，将弦的左右端点横坐标用结构体存起来。然后，将第一个雷达放在排序后的弦投影在x轴的右端点temp。从过第2个岛屿的弦的投影开始扫描，如果右端点

           <temp即右端点在雷达左边。把雷达移动到此右端点，此时就能使雷达既覆盖到这个岛屿，又覆盖到前面的岛屿。如果左端点在雷达右边，则不能覆盖，需要再建立一个

            雷达。然后把新雷达建在此时弦右端点投影到x轴的坐标。忽略前面的，对后面的岛屿进行同样的操作。（贪心思想）

注意：半径和坐标都有可能是小数，所以用double类型比较好，不然用int又要注意计算时*1.000变为浮点数。

代码：

#include<cstdio>

#include<iostream>

#include<cstring>

#include<algorithm>

#include<cmath>

using namespace std;



struct point

{

    double left;

    double right;

}p[5012];

bool flag;

int cnt;



bool cmp(point &x,point &y)

{

    return x.left<y.left;

}



int main()

{

    int cases=0,i,n;

    double d;

    while(scanf("%d%lf",&n,&d)&&n&&d)

    {

        flag=true;

        double a,b;

        for(i=0;i<n;i++)

        {

            scanf("%lf%lf",&a,&b);

            if(fabs(b)>d)

	    flag=false;

            p[i].left=a-sqrt(d*d-b*b);

            p[i].right=a+sqrt(d*d-b*b);

        }

	printf("Case %d: ",++cases);

	if(!flag)

	    puts("-1");

	else

	{

	    sort(p,p+n,cmp);

	    double temp=p[0].right;

	    cnt=1;

	    for(i=1;i<n;i++)

	    {

		if(p[i].right<temp)

		   temp=p[i].right;

		else if(p[i].left>temp)

	        {

		   cnt++;

		   temp=p[i].right;

		}

	    } 

	    printf("%d\n",cnt);

	}

    }

    return 0;

}





//AC

 

 

 

11920732

fukan

1328

Accepted

188K

32MS

C++

981B

2013-08-05 00:20:15