记录近期小改Apriori至MapReduce上的心得
·背景
前一阵,一直在研究一些ML的东东,后来工作关系暂停了一阵。现在继续把剩下一些热门的算法再吃吃透,"无聊+逗比"地把他们搞到MapReduce上。这次选择的入手对象为Apriori,也就是大家俗称的"关联规则挖掘",有别于CF(协同过滤)的正交输出。再俗一点,就是常被人提及的"啤酒+面包"的故事。
·Apriori算法简介
在关联规则挖掘方面,有两项著名的算法:Apriori和FPgrowth。两者各有特点,由于计算量级别的差异,越来越多的人选择了后者。但这并不意味着Apriori就是垃圾。个人的理解,FPgrowth为MP而生,Apriori为容器而生。当单日志量达到5G,10G以上Apriori在计算方面的吃亏逐步显现,即便如此,对于人们对于尽可能减少Apriori扫描次数的优化机制仍然乐此不疲。尤其是作为容器方面的选择,可以极大的减少整个代码的实现过程和增加可读性,同时又能训练你的脑力和对容器的使用创意。
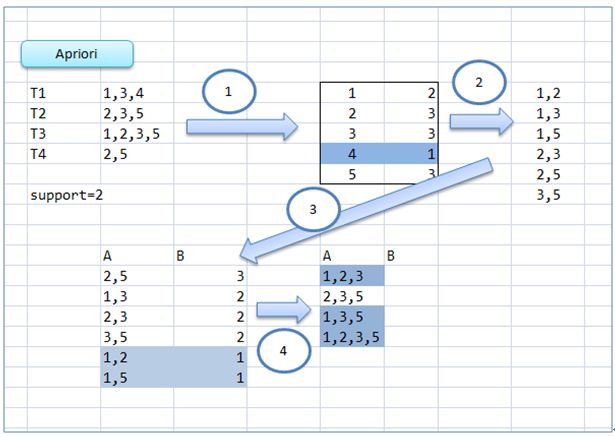
作为单机版本来说,整体Apriori的逻辑过程如上所述,相比"树"和"图"来说要简单许多,但是仍然暗藏不少重复计算的陷阱。
- 基本条件,有交易记录T和自己设定的支持度support。
- 从1维最小元素开始做group by+count(*),得到统计集合
- 按support条件,把不符合条件的统计对象过滤掉,类似oracle having追加条件。
- 把渣过滤完毕后,做完全组合,也就是大家在初中时候学的完全唯一组合,得到频繁项组合。这其中你也可以自己设个条件,认为XXX就是最大的频繁项。
- 以这频繁项为基础,去扫描交易记录T,得到步骤2。以此反复,找到你想要的关联组合。

作为MP版来说,Apriopi如何压榨Map的资源,真是件令人头痛的事情。如上图所述:
- 每个Map DataNode都会得到最大的频繁项。如果整体交易记录构成是完全随机分布,那最后的C的数量会非常集中而且稳定。
- 不幸的是,你无法保证十几,几十G的交易T中的交易习惯,一定是随机均匀分布,如果是正态、泊松、二项式等等。那C中最大项集合数量会猛增。
- 这时候,必须在从Map DataNode中继续过一遍集合,删除干扰度较高的最大频繁项,尽量找到唯一最大频繁。
· 一些心得体会
- 就像拍照一样,要先构图。整段代码在把小孩子哄睡后花了近一周时间才完成。其中6成时间用于数据结构设计,3成时间用来code,1成用来调试。
- 数据结构返工两次,最后剑走偏锋。楼主逗比地用了二维set,网上都了一把,用的人不多,不是那种new出来的不带属性那种,而是set套set,和map套set。极尽c++容器之能事。感觉好的数据结构,至少少写200行代码。代码思路: C[频繁set<set>]-> [Struct/raw_c] -> Map<set,int> -> L -> set<set>
- 如何减少计算量是件恶心的事,把文本入内存需要一次N量计算,扫面一次就是N量。整个Apriorio的计算至少K·N,着实笨重,这还不算不少代码洁癖的爱好,还会反复叠加计算量。
- 附属的是一个单机版的Apriori,MP的就补贴了,思路如上图所述。在生产环境中还需要考虑到hadoop的输出限制和函数返回值形式,需要尽可能使用引用和指针,减少内存交互。
- 官网有提到支持度这个概念,当然大家也可以完全按照自己的意愿做一些改动和设定,条条大道去罗马,基本就这个模式了。
· 单机版 centos 6(2.6)+gcc433
#include <iostream>
#include <sstream>
#include <fstream>
#include <string.h>
#include <vector>
#include <map>
#include <set>
#include <algorithm>
using namespace std;
typedef struct { //原始集合结构定义
vector<string> ss;
} t_raw_jh;
typedef struct { //有效数据/统计集合定义
set<string> ss;
int sup_num;
} t_raw_tj;
t_raw_jh raw_c[50]; //原始数据
map<set<string>,int> raw_cnt_base; //原始元素统计集合
t_raw_tj L[10]; //洗出来的单集合组合
//set<set> new_kc; //洗出来的排列对象集,作为下次扫描的催化剂
int raw_num=0; //原始数据计数器
int l_num=0; //统计数据计算器
int raw_msup=2; //频繁项支持度
/* C[频繁set<set>]-> [Struct/raw_c] -> Map<set,int> -> L -> set<set> */
void CountEleBase(string line,const char* delim,int raw_num); //1+pre,把一条元素洗到二维颗粒,同时统计group by count
void CountEleReal(set<set<string> > &cc); //1+real,根据3的催化剂,扫描原始记录,同时统计group by count
int WashEleBase(); //2,把MAP SORT[group by count]洗出大于支持度的对象集
set<set<string> > GetNewKc(int size); //3,把洗出的对象集合,极限排列出所有可能,作为下次扫描的催化剂
void Display(); //显示原始集合、单元素非排序group by count
void ClearTj(); //把统计表给清空
void RunApriori(set<set<string> > &fc); //嵌套跑,当然也可以迭代WHILE跑,入参为频繁项
int main()
{
std::ios::sync_with_stdio(false);
string filename="./ap001.txt";
string line;
ifstream ifs;
ifs.open(filename.c_str());
while(getline(ifs,line))
{
CountEleBase(line,",",raw_num);
raw_num++;
}
// Display();
//得到第一组经过支持度过滤的C
set<set<string> > aaa; //频繁项,根据有效支持元素得出的组合
aaa=GetNewKc(WashEleBase());
RunApriori(aaa);
}
void RunApriori(set<set<string> > &fc)
{
if(l_num==1) return;
CountEleReal(fc);
fc.clear();
fc=GetNewKc(WashEleBase());
RunApriori(fc);
}
void CountEleReal(set<set<string> > &cc)
{
//扫描记录集
cout<<"\n-----扫描记录集-----"<<endl;
//迭代器定义好,在该函数内之后会用到
set<set<string> >::iterator ot_it;
set<string>::iterator in_it;
raw_cnt_base.clear();
for(ot_it=cc.begin();ot_it!=cc.end();ot_it++)
{
int map_cc=0;
for(int i=0;i<raw_num;i++)
{
vector<string>::iterator res;
for(res=raw_c[i].ss.begin();res!=raw_c[i].ss.end();res++)
{
cout<<*res<<" ";
}
cout<<"|";
int map_in_cc=0;
for(in_it=(*ot_it).begin();in_it!=(*ot_it).end();in_it++)
{
cout<<*in_it<<" ";
res=find(raw_c[i].ss.begin(),raw_c[i].ss.end(),*in_it);
if(res!=raw_c[i].ss.end()) map_in_cc++;
}
if(map_in_cc==(*ot_it).size()) map_cc++;
cout<<"|"<<map_in_cc<<endl;
}
raw_cnt_base[*ot_it]=map_cc;
cout<<"-->"<<map_cc<<endl;
}
}
set<set<string> > GetNewKc(int size)
{
vector<string>::iterator ss_it;
set<string> kk[size];
set<set<string> > new_kc;
int pi=0;
set<string>::iterator kk_it;
//做两两极限排列组合
for(int i=0;i<l_num;i++)
{
set<string> tmp=L[i].ss;
for(int j=i+1;j<l_num;j++)
{
for(kk_it=L[j].ss.begin();kk_it!=L[j].ss.end();kk_it++)
{
tmp.insert(*kk_it);
}
new_kc.insert(tmp);
tmp=L[i].ss;
}
}
cout<<"有效支持元素 ---> C组合[频繁项]:"<<endl;
set<set<string> >::iterator out_it;
set<string>::iterator in_it;
for(out_it=new_kc.begin();out_it!=new_kc.end();out_it++)
{
for(in_it=(*out_it).begin();in_it!=(*out_it).end();in_it++)
{
cout<<*in_it<<",";
}
cout<<endl;
}
return new_kc;
}
int WashEleBase()
{
map<set<string>,int>::iterator raw_cnt_it;
int i=0;
l_num=0;
ClearTj();
for(raw_cnt_it=raw_cnt_base.begin();raw_cnt_it!=raw_cnt_base.end();raw_cnt_it++)
{
if(raw_cnt_it->second>=raw_msup)
{
L[i].ss=raw_cnt_it->first;
L[i++].sup_num=raw_cnt_it->second;
l_num++;
}
}
//Display
cout<<"有效支持元素:"<<endl;
set<string>::iterator ss_it;
for(i=0;i<l_num;i++)
{
for(ss_it=L[i].ss.begin();ss_it!=L[i].ss.end();ss_it++)
{
cout<<*ss_it<<",";
}
cout<<"|"<<L[i].sup_num<<endl;
}
return i;
}
void CountEleBase(string line,const char* delim,int raw_num)
{
char *p=NULL,*q=NULL;
p=const_cast<char*>(line.c_str());
while(p)
{
q=strsep(&p,",");
set<string> load_ss;
raw_c[raw_num].ss.push_back(q);
load_ss.insert(q); raw_cnt_base[load_ss]++;
}
}
void Display()
{
cout<<"----Print Map-------"<<endl;
map<set<string>,int>::iterator raw_cnt_it;
set<string>::iterator ss_it;
for(raw_cnt_it=raw_cnt_base.begin();raw_cnt_it!=raw_cnt_base.end();raw_cnt_it++)
{
for(ss_it=(raw_cnt_it->first).begin();ss_it!=(raw_cnt_it->first).end();ss_it++)
{
cout<<*ss_it<<" ";
}
cout<<":"<<raw_cnt_it->second<<endl;
}
//raw_cnt_base.clear();
cout<<"----Print Raw-------"<<endl;
vector<string>::iterator raw_c_it;
for(int i=0;i<raw_num;i++)
{
for(raw_c_it=raw_c[i].ss.begin();raw_c_it!=raw_c[i].ss.end();raw_c_it++)
{
cout<<*raw_c_it<<" ";
}
cout<<endl;
}
}
void ClearTj()
{
for(int i=0;i<10;i++)
{
L[i].sup_num=0;
L[i].ss.clear();
}
}
· 另
望各位路过的大侠,嘴上留情,手上斧正,看看能否进一步压缩计算空间量~~。^_^。