Render OpenCascade Geometry Curves in OpenSceneGraph

在OpenSceneGraph中绘制OpenCascade的曲线

Render OpenCascade Geometry Curves in OpenSceneGraph

[email protected]

摘要Abstract：本文简要说明OpenCascade中几何曲线的数据，并将这些几何曲线在OpenSceneGraph中绘制出来。 

关键字KeyWords：OpenCascade、Geometry Curve、OpenSceneGraph、B-Spline、NURBS 

一、引言 Introduction

结合《BRep Format Description White Paper》对OpenCascade中的几何数据结构有详细的介绍。OpenCascade中BRep格式中的曲线总共分为九种，不过有二维三维之分： 

1．直线 Line 

2．圆 Circle 

3．椭圆 Ellipse 

4．抛物线 Parabola 

5．双曲线 Hyperbola 

6．Bezier曲线 Bezier Curve 

7．B-Spline曲线 B-Spline Curve 

8．裁剪曲线 Trimmed Curve 

9．偏移曲线 Offset Curve 

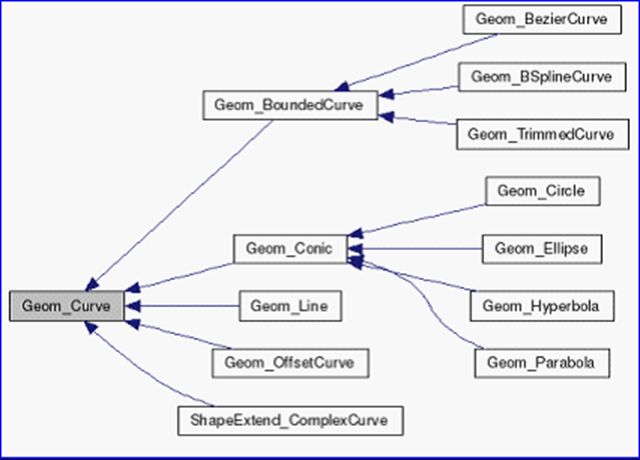
曲线的几何数据都有一个抽象基类Geom_Curve，类图如下所示： 

Figure 1.1 Geometry curve class diagram 

抽象基类Geom_Curve有几个纯虚函数FirstParameter()、LastParameter()、Value()，根据这几个虚函数，就可以计算曲线上对应参数U的值。类图如下图所示： 

Figure 1.2 Geom_Curve Inherited class diagram 

每种曲线都对那些纯虚函数进行实现，使计算曲线上点的方式统一。 

二、程序示例 Code Example

根据抽象基类Geom_Curve的几个纯虚函数： 

1．FirstParameter(); 

2．LastParameter(); 

3．Value(u); 

利用多态可将曲线上点都以统一的方式计算出来，并使用GL_LINE_STRIP绘制出来。示例程序如下所示：

/*

*    Copyright (c) 2013 eryar All Rights Reserved.

*

*        File    : Main.cpp

*        Author  : [email protected]

*        Date    : 2013-08-09 18:09

*        Version : 1.0v

*

*    Description : Draw OpenCascade Geometry Curves in OpenSceneGraph.

*                  

*/



// OpenSceneGraph library.

#include <osgDB/ReadFile>

#include <osgViewer/Viewer>

#include <osgViewer/ViewerEventHandlers>

#include <osgGA/StateSetManipulator>



#pragma comment(lib, "osgd.lib")

#pragma comment(lib, "osgDbd.lib")

#pragma comment(lib, "osgGAd.lib")

#pragma comment(lib, "osgViewerd.lib")



// OpenCascade library.

#include <TColgp_Array1OfPnt.hxx>

#include <TColStd_Array1OfReal.hxx>

#include <TColStd_Array1OfInteger.hxx>



#include <Geom_Circle.hxx>

#include <Geom_Ellipse.hxx>

#include <Geom_Hyperbola.hxx>

#include <Geom_Parabola.hxx>

#include <Geom_BezierCurve.hxx>

#include <Geom_BSplineCurve.hxx>



#pragma comment(lib, "TKernel.lib")

#pragma comment(lib, "TKMath.lib")

#pragma comment(lib, "TKG3d.lib")



// Curve Segment Delta.

const double CURVE_SEGMENT_DELTA = 0.01;



/*

* @brief Build geometry curve of OpenCascade.

*/

osg::Node* buildCurve(const Geom_Curve& curve)

{

    osg::ref_ptr<osg::Geode> geode = new osg::Geode();

    osg::ref_ptr<osg::Geometry> linesGeom = new osg::Geometry();

    osg::ref_ptr<osg::Vec3Array> pointsVec = new osg::Vec3Array();



    gp_Pnt point;

    double dFirst = curve.FirstParameter();

    double dLast = curve.LastParameter();



    Precision::IsNegativeInfinite(dFirst) ? dFirst = -1.0 : dFirst;

    Precision::IsInfinite(dLast) ? dLast = 1.0 : dLast;

    

    for (double u = dFirst; u <= dLast; u += CURVE_SEGMENT_DELTA)

    {

        point = curve.Value(u);



        pointsVec->push_back(osg::Vec3(point.X(), point.Y(), point.Z()));

    }



    // Set the colors.

    osg::ref_ptr<osg::Vec4Array> colors = new osg::Vec4Array;

    colors->push_back(osg::Vec4(1.0f, 1.0f, 0.0f, 0.0f));

    linesGeom->setColorArray(colors.get());

    linesGeom->setColorBinding(osg::Geometry::BIND_OVERALL);



    // Set the normal in the same way of color.

    osg::ref_ptr<osg::Vec3Array> normals = new osg::Vec3Array;

    normals->push_back(osg::Vec3(0.0f, -1.0f, 0.0f));

    linesGeom->setNormalArray(normals.get());

    linesGeom->setNormalBinding(osg::Geometry::BIND_OVERALL);



    // Set vertex array.

    linesGeom->setVertexArray(pointsVec);

    linesGeom->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::LINE_STRIP, 0, pointsVec->size()));

    

    geode->addDrawable(linesGeom.get());



    return geode.release();

}



/**

* @breif Build geometry curve of OpenCascade.

*/

osg::Node* buildScene()

{

    osg::ref_ptr<osg::Group> root = new osg::Group();



    // 1. Build circle curve.

    Geom_Circle circle(gp::YOZ(), 1.0);



    root->addChild(buildCurve(circle));



    // 2. Build ellipse curve.

    Geom_Ellipse ellipse(gp::ZOX(), 1.0, 0.3);



    root->addChild(buildCurve(ellipse));



    // 3. Build Hyperbola curve.

    Geom_Hyperbola hyperbola(gp::XOY(), 1.0, 0.6);



    root->addChild(buildCurve(hyperbola));



    // 4. Build parabola curve.

    Geom_Parabola parabola(gp::ZOX(), 1.0);



    root->addChild(buildCurve(parabola));



    // 5. Build Bezier curve.

    TColgp_Array1OfPnt poles(1, 4);

    poles.SetValue(1, gp_Pnt(-1, -1, 0));

    poles.SetValue(2, gp_Pnt(1, 2, 0));

    poles.SetValue(3, gp_Pnt(3, 0, 0));

    poles.SetValue(4, gp_Pnt(4, 1, 0));

    Geom_BezierCurve bezierCurve(poles);



    root->addChild(buildCurve(bezierCurve));



    // 6. Build BSpline curve.

    TColgp_Array1OfPnt ctrlPnts(1, 3);

    TColStd_Array1OfReal knots(1, 5);

    TColStd_Array1OfInteger mults(1, 5);

    

    ctrlPnts.SetValue(1, gp_Pnt(0, 1, 0));

    ctrlPnts.SetValue(2, gp_Pnt(1, -2, 0));

    ctrlPnts.SetValue(3, gp_Pnt(2, 3, 0));



    knots.SetValue(1, 0.0);

    knots.SetValue(2, 0.25);

    knots.SetValue(3, 0.5);

    knots.SetValue(4, 0.75);

    knots.SetValue(5, 1.0);



    mults.Init(1);



    Geom_BSplineCurve bsplineCurve(ctrlPnts, knots, mults, 1);



    root->addChild(buildCurve(bsplineCurve));



    return root.release();

}



int main(int argc, char* argv[])

{

    osgViewer::Viewer myViewer;



    myViewer.setSceneData(buildScene());



    myViewer.addEventHandler(new osgGA::StateSetManipulator(myViewer.getCamera()->getOrCreateStateSet()));

    myViewer.addEventHandler(new osgViewer::StatsHandler);

    myViewer.addEventHandler(new osgViewer::WindowSizeHandler);



    return myViewer.run();

}

因抛物线和双曲线的FirstParameter()和LastParameter()为负无穷和正无穷，所以对其进行处理，只输出了部分曲线。 

程序效果如下图所示： 

Figure 2.1 OpenCascade Geometry Curves in OpenSceneGraph 

三、结论 Conclusion

OpenCascade的几何数据使用还是很方便的，只要将相应的曲线构造出来之后，计算曲线上的点使用函数Value()即可，还可计算相应参数处的微分值等。 

通过理解《BRep Format Description White Paper》，可将BRep文件中数据导入OpenCascade中与上面实现的程序进行对比，结果正确。如下图所示： 

Figure 3.1 B-Spline in OpenSceneGraph 

Figure 3.2 B-Spline in OpenCascade Draw 

 

PDF Version: Draw OpenCascade Geometry Curves in OpenSceneGraph