字符串匹配问题-KMP总结
用意:总结一些学习KMP的一些感悟,想尽量把KMP讲清楚,欢迎指正。以后字符串匹配的相关内容都在此处记录着。
如何计算回溯表,即如何计算最长前缀?
一、问题描述
在字符串Str(长度为n)中找到字符串Target(长度为m)的位置。通常假设n>=m。
字符串Str, Target的字符属于字符空间集合S, S的大小为N。
在文本编辑器中经常使用。
不错的说明例子是阮一峰- 字符串匹配的KMP算法。
二、问题推导
基本思路:设置一个位移s=0;从Target中取出一个字符,然后从Str[s]中拿出一个字符来与之匹配,一旦Str到达结尾或者不匹配,则匹配结束,Str位移s加1,直到匹配结束。【注:需要判断Target是否为空,是则直接判定匹配成功】
例子:糟糕的情况是匹配的N个字符后,最后一个字符匹配错误,如下图BAAAA匹配了5个字符而在第六个字符匹配失败后,需要回溯N-1即4个字符,再进行4轮匹配后才结束Str前五个字符的匹配,总共浪费了5+4+3+2=14次比较。
朴素的字符串匹配的时间复杂度上限为O((n-m) * m),空间复杂度为O(1); 而KMP算法的时间复杂度为O(m) + O(n),空间复杂度为O(m),(适用于n >> m情况,这个条件一般都成立)。O(m)为数据预处理时间。 O(n)为数据搜寻时间。
注:实际问题中朴素字符串使用很普遍。原因:如果字符S空间N不小且Str字符随机分布时,朴素的字符串匹配时间复杂度为O(n),由于不匹配情况会很早出现,回溯长度基本为0或者1. 回溯一个字符的概率为1/N(英文字幕26个,中文常用汉字3000个,回溯概率很小)。所以一般的文本编辑器使用朴素字符串匹配即可,只进行O(n)次比较。
当然了,如果是匹配DNA的话,DNA链只有C、G、T、A四个碱基,KMP就能派上用场了。
KMP的基本思想:当发生一次失配且已匹配了q(q>=2)个字符时,无需回退q-1步,应充分利用已匹配的q个字符与Str和Target字符串均相等的重要信息,即已匹配的数据包含了下一步回溯的步数j。KMP的核心就是通过对Target进行预处理找到这个T[1...m-1]回溯表。
例子:
s 01 2345
Str: BAAAAB
m 0 1 2345
Tar: BAAAAA
按照朴素字符串匹配,s表示Str的位移,初始化为0。Str与Tar进行匹配,在m=5时发生适配,那么s=1,m置0,Tar[m=0]‘B’将与Str[s=1]‘A’进行比较,其实由于Str和Tar的字符0~4已一致,那么比较等价于Tar[m=0]‘B’与Tar[s=1] 'A'比较,发现失配s=2,m=0,我们发现直到s=5时,才需要使用Str字符串,因为Str[5]和Tar[5]不一样了。所以,我们只使用Tar,让Tar[0]与Tar[1...4]进行比较,发现均适配,那么一旦发生了第6个字符失配的情况,无需回溯,即s设置为s + q(匹配字符q = 5)即可。
上述例子只说明了一种单字符失配特例,如果已匹配字符串为Str:ABCADDAB时,虽然Str[0]与Str[3]匹配,但是Str[1]与Str[4]不匹配,所以不会将j=3作为回溯值。真正的回溯值是通过找到满足如下条件的最长后缀,条件:最长前缀移动j(j>=0)后可以在q个匹配字符中找到等价的最长后缀。
考虑到方便同时计算s和m(后面算法描述部分可以看到计算最长前缀的优势)
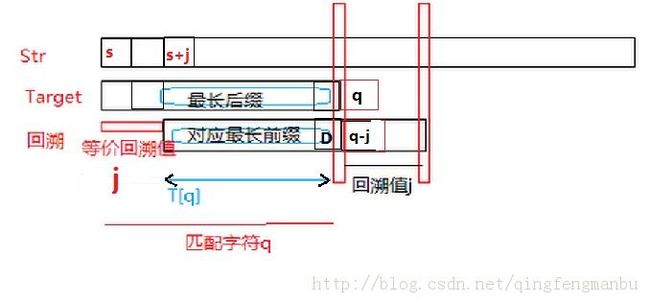
回溯表T记录最长前缀的长度减1,如ABAB的最长前缀为AB,那么T[4] = 2- 1 = 1,如果使用以0开始的数组的话T[4]本质上即最长前缀"AB"末尾下标(图中位置D):
T[q] = q(匹配字符) - j(回溯值) [图中j=2;特例,T[0] = -1,保证s = s + 1]
如下图所示,那么Str的下一个初始位移为 s + j = s + q - T[q] ,Target的下一个比较位置为q - j = T[q](q>=1)
那么Str的下一个要和Target[q-j]比较的位置为Str[s + j + q - j] = Str[s + q],永远不回退。
如何计算回溯表,即如何计算最长前缀?
回溯表计算方法:回溯表可以保证Str的每一个元素只比较一次。【本质上预处理Target中多次比较了Str元素】
使用归纳法进行推导:以Target=“ABCDABD”求解T[0...7]为例。设置特例T[0] = -1,由于"A"最长前缀和后缀均为0且最长前缀为"A",末尾下标为0,那么T[1] = 0。知道T[0]与T[1]后可以推导出T[2],已知"A"的最长前缀为"A",末尾下标为i(i=0),那么判断Target[T[2-1]+1]="A"与Target[2-1]是否相等,如果相等那么前缀和后缀均延长1,T[2] = T[2-1] + 1。如果直到T[0....i-1](i >= 2),那么可以通过递归求出T[i]。比较Target[i-1] 与Target[T[i-1] + 1], 若相等则T[i] = T[i-1] + 1。a. 否则比较T[i-1]是否为0,结束,T[i] = 0结束,否则比较Target[i-1]与Target[T[i-1] + 1],循环a位置。
回溯表由此可以计算。
三、算法描述
回溯表伪代码
返回数据:回溯表T[0~strlen(target)-1]
create_table (字符串 target) // N为字符串target的长度
cnd = 0 // cnd表示字符串target的下标,0~strlen(target)-1
pos = 2 // pos表示回溯表的下标
T[0] = -1; T[1] = 0 //初始化
while pos < strlen(target)
do if Target[pos-1] == Target[cnd]
then T[pos] = cnd + 1
cnd = cnd + 1
pos = pos + 1
else if cnd > 0
then cnd = T[cnd]
else
then T[pos] = 0; pos = pos + 1
KMP伪代码
返回数据:若str中存在target,那么返回第一次出现的位置;否则返回NULL
kmp_search (字符串 str, 匹配字符串 target)
do if strlen(target) == 0
then return address(str)
n = strlen(str) // n为str的长度
m = strlen(target) // m为target的长度
i = 0 // i 为str的下标
s = 0 // s为str的位移
while s <= n-m:
while str[s+i] == target[i]:
do if i+1 == m then
return address(str) + s
else then
i = i + 1
s = s + i - T[i]
do if i > 0 then
i = T[i]
else then
i = 0
return NULL
四、基本代码
#include <stdio.h>
/**
len < 0, return null;
*/
int *kmp_table(const char* target, int len) {
int* T = (int*)malloc(len * sizeof(int));
T[0] = -1, T[1] = 0;
int cnd = 0; /* the zero-based index in W */
int pos = 2; /* the current position we are computing in T */
while (pos < len) {
if (target[pos - 1] == target[cnd]) {
T[pos++] = ++cnd;
} else if (cnd > 0) {
cnd = T[cnd];
} else {
T[pos++] = 0;
}
// printf("T[%d] = %d\n", pos-1, T[pos-1]);
}
return T;
}
int qing_strlen(char* str) {
int count = 0;
char* p = str;
while(p[count] != '\0') count++;
return count;
}
int qing_str_equal(char* str, char* target, int target_len) {
int count = 0;
while (str[count] != '\0' && target[count] != '\0' && str[count] == target[count])
count++;
return count;
}
char* qing_strstr(char* str, char* target) {
/* defense code 1 */
if (target[0] == '\0') return str;
int str_len = qing_strlen(str);
int target_len = qing_strlen(target);
int *T = kmp_table(target, target_len);
int s = 0; //shift of str
int i = 0; // index of target
/* navie strstr method
for (s = 0; s < str_len - target_len; s++) {
if (qing_str_equal(str+s, target, target_len) == target_len)
printf("result=%d\n", s);
}
*/
/* kmp method */
while (s <= str_len - target_len) {
while (str[s+i] == target[i]) {
if (i+1 == target_len)
return str + s;
else
i++;
}
s += (i - T[i]);
if (i > 0)
i = T[i];
else
i = 0;
}
free(T);
return NULL;
}
int main() {
char* str = "aaaaaaaaaaaaaaaaaaaaaaaaaaab";
char* target = "aaaaaaaaaaaaaaab";
if (str==NULL || target == NULL) exit(-1);
int count = 0;
char* p = str;
if (target[0] == '\0')
printf("null result=%d", str == strstr(str, target));
else {
while ((p = strstr(p, target)) != NULL) {
count++;
p++;
}
printf("count=%d\n", count);
}
system("pause");
return 0;
}
五、测试用例
平时想想测试用例,可以很好地提升代码通过边界测试的能力。
测试用例:
1. 空字符串:target为""或者str为"",三种情况。
2. 单字符串 : str = "aaa" ,target="a",或反转。
3. 一些复杂组合: str="abcdaedfasdsdfsabab", target="abab"
4. 最差字符串:str="aaaaaaaaaaaaaaaaaaaaaaaaaaaa"与target="aaaaaaaaaaaaaaab"
六、实战练习
1. leetcode练习题strstr http://oj.leetcode.com/problems/implement-strstr/
class Solution {
public:
int *kmp_table(const char* target, int len) {
int* T = (int*)malloc(len * sizeof(int));
T[0] = -1, T[1] = 0;
int cnd = 0; /* the zero-based index in W */
int pos = 2; /* the current position we are computing in T */
while (pos < len) {
if (target[pos - 1] == target[cnd]) {
T[pos++] = ++cnd;
} else if (cnd > 0) {
cnd = T[cnd];
} else {
T[pos++] = 0;
}
}
return T;
}
int qing_strlen(char* str) {
int count = 0;
char* p = str;
while(p[count] != '\0') count++;
return count;
}
int qing_str_equal(char* str, char* target, int target_len) {
int count = 0;
while (str[count] != '\0' && target[count] != '\0' && str[count] == target[count])
count++;
return count;
}
char *strStr(char *haystack, char *needle) {
// IMPORTANT: Please reset any member data you declared, as
// the same Solution instance will be reused for each test case.
/* defense code 1 */
if (needle[0] == '\0') return haystack;
int haystack_len = qing_strlen(haystack);
int needle_len = qing_strlen(needle);
int *T = kmp_table(needle, needle_len);
int s = 0; //shift of str
int i = 0; // index of target
/* navie strstr method
for (s = 0; s < str_len - target_len; s++) {
if (qing_str_equal(str+s, target, target_len) == target_len)
printf("result=%d\n", s);
}
*/
/* kmp method */
while (s <= haystack_len - needle_len) {
while (haystack[s+i] == needle[i]) {
if (i+1 == needle_len)
return haystack + s;
else
i++;
}
s += (i - T[i]);
if (i > 0)
i = T[i];
else
i = 0;
}
free(T);
return NULL;
}
};
七、参考资料
[1] Princeton Algorithms http://algs4.cs.princeton.edu/home/
[2] KMP en.wikipedia.org http://en.wikipedia.org/wiki/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm
[3] 阮一峰 字符串匹配的KMP算法 http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html