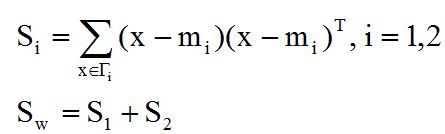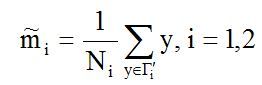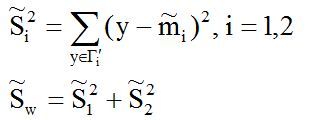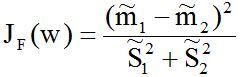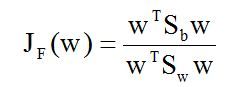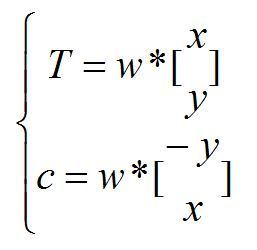【模式识别】学习笔记(3)>>>【Fisher线性判别】

问题预备：

        如果考虑把d维空间的样本投影到一条直线上，形成一维空间，即把维数压缩到一维。
然而：

        1、即使样本在d维空间里形成若干紧凑的互相分得开的集群，当把它们投影到一条直线上时，也可能会是几类样本混在一起而变得无法识别。

        2、但是，在一般情况下，总可以找到某个方向，使在这个方向的直线上，样本的投影能分得开

生成随机样本：

        比如，我们通过MATLAB生成随机的两类模式样本集：

        （该样本简单加入了高斯噪声以模拟系统总噪声和特征的不完全相关性）

o1=[3 4],o2=[8,2];
N1=15;N2=15;
N=N1+N2;
points=[abs(randn(N ,1)) rand(N,1)];
points(:,1)=points(:,1)*sqrt((o2(2)-o1(2))^2+(o2(1)-o1(1))^2)/5;
points(:,2)=points(:,2)*2*3.14;
pointso1=points(1:N1,:);
pointso2=points(N1+1:end,:);
pointso1xy=o1(1)+pointso1(:,1).*cos(pointso1(:,2));
pointso1xy=[pointso1xy o1(2)+pointso1(:,1).*sin(pointso1(:,2))];
pointso2xy=o2(1)+pointso2(:,1).*cos(pointso2(:,2));
pointso2xy=[pointso2xy o2(2)+pointso2(:,1).*sin(pointso2(:,2))];
plot(pointso1xy(:,1),pointso1xy(:,2),'.r');hold on;
plot(pointso2xy(:,1),pointso2xy(:,2),'.g');

        如图：

        通过调整第三行中r分量的比例因子，我们可以获得可分辨度等低的模式样本集：

        这里我们使用前一种样本。

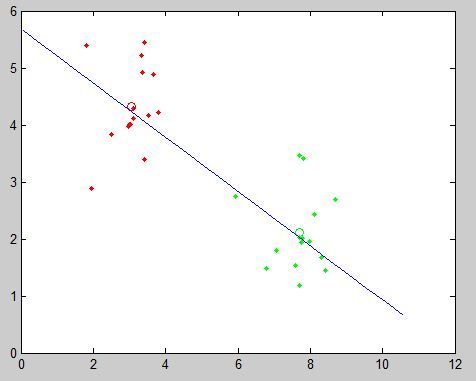
        那么，如何根据实际情况找到一条最好的、最易于分类的投影线，这就是Fisher判别方法所要解决的基本问题。

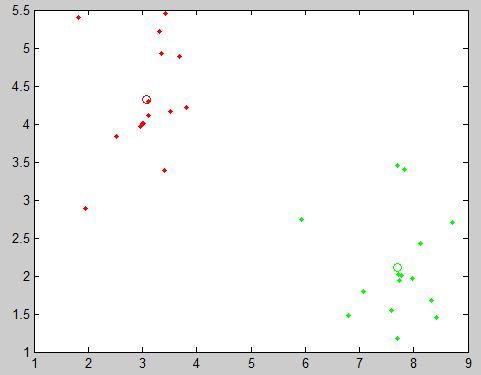
        先来看下最终的分类结果，图中直线就是我们求得的投影直线，蓝色圈圈就是阈值所处位置：

如何求得从高维到一维的变换关系？

        对于该例子，从d维空间到一维空间的一般数学变换方法：

                假设有一集合Г包含N=30个2维样本x1, x2, …, xN，

                其中N1=15个属于ω1类的样本记为子集Г1， N2=15个属于ω2类的样本记为子集Г2 。

                若对xn的分量做线性组合可得标量：
                                                                        yn = wTxn, n=1,2,…,N
        这样便得到30个一维样本yn组成的集合，并可分为两个子集Г1’和Г2’ 。
        实际上，w的值是无关紧要的，它仅是yn乘上一个比例因子，向量里决定长短，重要的是选择w的方向，也叫方向角。

        很明显的是，w的方向不同很影响分类结果。

        于是在数学上，这就是寻找最好的变换向量w*的问题。

那么，如何求解w*呢？

        首先我们来看一堆公式推导，不喜欢的完全可以跳过，后面会有你想要的东西的。

        （1）首先是，各类样本的均值向量mi：

        很明显，这其实就是在求一个聚类中心，注意是均值向量。

        反映到matlab里就是这样：

m1=sum(pointso1xy)/N1;
m2=sum(pointso2xy)/N2;

        如下获得其直观图像，图中的红圈和绿圈就是所求的聚类中心啦：

        （2） 样本类内离散度矩阵Si和总样本类内离散度矩阵Sw：

        其中Sw是对称半正定矩阵，而且当N>d时通常是非奇异的。

        对于一维来说离散度矩阵对应的就是离差平方和/方差：

s1=sum([pointso1xy(:,1)-m1(1) pointso1xy(:,2)-m1(2)].^2);s1=sum(s1(:));
s2=sum([pointso2xy(:,1)-m1(1) pointso2xy(:,2)-m1(2)].^2);s2=sum(s2(:));

        （3） 样本类间离散度矩阵Sb ：

        Sb是对称半正定矩阵。

sb=sum(((m1-m2).^2)');

引出Fisher准则函数

        分类得好不好，怎么分类，怎么确定判别函数？这一切都在变换后的一维Y空间上进行，

        而对于我们即将映射的一维Y空间有：

            （1） 各类样本的均值：

            （2） 样本类内离散度和总样本类内离散度

            于是，Fisher准则函数定义为：

        其中，分子是两类均值之差平方，分母是样本类内离散度之和。显然，应该使JF(w)的分子尽可能大而分母尽可能小，这样才使得类别之间不仅离得远，而且类内样本聚集紧密，即应寻找使JF(w)尽可能大的w作为投影方向。但上式中并不显含w，因此须设法将JF(w)变成w的显函数。

        将上述各式代入JF(w)，可得：

        于是问题转化为准则函数的极值问题，当其取极大值时的w*就是我们要的东西了。

Lagrange乘数法求解极值问题：

        求得一个函数的极值最容易想到的就是采用导数求解，而对于许多实际的问题，也常用拉氏乘数法求解。

        我们令分母等于非零常数，即：

        定义Lagrange函数为：

        也就是转化为求L函数极值问题，其中λ为Lagrange乘子。将上式对w求偏导数且令其为0，可得：

        因为Sw非奇异，所以有：

        有没有发现这变成了求矩阵特征值的问题了呢？我们带入前边的公式：

        显然，R是一个标量，即Sbw*实际上跟m1-m2是同方向的，注意m1,m2,w*都是列向量，而前面的代码为了方便编写都是作为行向量处理。然后我们更新下特征方程：

        此处声明下，我们的任务是寻找最佳的投影方向，跟向量的模长并无关系，而上式除去比例因子R/λ之后就剩：

        对于此处二维转一维的情况，Sw也是个标量，m1-m2为两聚类中心的向量差。也就是从m2到m1的向量。

求得投影直线与变换样本y：

        那么可得一直线方程：

c=w2*x-w1*y

        将其画在图上是这样的：

        于是我们变换下，并简单地取下阈值：

y1=w*pointso1xy';
y2=w*pointso2xy';
T=(min(y1(:))+max(y2(:)))/2;

        至此，我们求出了变换关系w和一维分类阈值T。

标记阈值点

        有趣的是，这样我们还并不满足，有人一定会想在Figure中标出阈值点，然而T=w*pointxy这样的运算显然不可逆，即无法求出向量pointxy。

        那么，还记得前面求得的直线方程吗？

        联立：

        用行列式解的优点就是没有那么多if语句需要考虑，一个判别式解决一切：

        因此，整个工作完成：