counting sort (计数排序) algorithm
假设n个输入元素中每一个均介于0~k之间,k为最大值,这里k为整数。如果k=O(n), 则计数排序的运行时间为θ(n)。
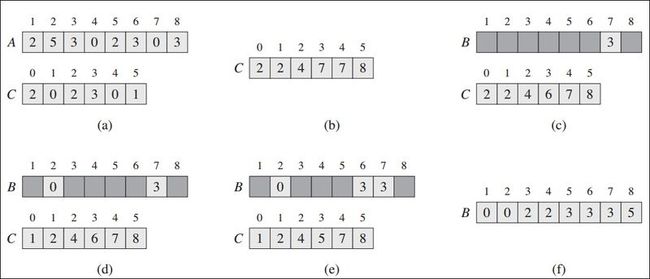
计数排序的核心思想是:对于每个元素x,统计出小于等于x元素的个数,利用该信息,就可以确定每个元素x在最终数组中的位置。比如小于等于x的元素个数有17个,则该元素的最终位置在17-1=16.
计数排序的伪代码如下:
其中数组A为输入数组,数组B为排序后输出数组,k为数组A元素中最大值,伪代码中少个数组长度的参数,自行加上。
line 4~5 统计数组A中每个元素A[j]出现次数.
line 7~8 统计数组A中小于等于i(<0i<k)的元素个数.
line 10~12 根据小于等于A[j]的个数直接定位A中每个元素的位置,因为可能有相同元素,所以每次同时递减 小于等于A[j]的个数.
根据伪代码很同意得出计数排序的运行时间为θ(n)。
计数排序一个重要的特性就是它是稳定的: 相同值元素在最终数组中的相对次序同他们在输入数组中相同。
下面是数组A[] = {2,5,3,0,2,3,0,3}数组排序的全过程示意图:
个人代码如下:
/************************************************************************/
/* author: alex */
/* time: 1/9 2014 */
/************************************************************************/
#include <iostream>
using namespace std;
int count_sort(int array_src[], int array_dst[], int max_num_k, int array_length);
void print_array(int array[], int length);
int main(void)
{
int array_src[] = {2,5,3,0,2,3,0,3};
int array_length = sizeof(array_src)/sizeof(array_src[0]);
int max_num_of_array_src = 5; // get max from array_src.
int *array_dst = (int *)malloc(array_length*sizeof(int));
if(NULL == array_dst)
{
cout << "array_dst malloc error !" << endl;
return -1;
}
memset(array_dst, 0, array_length*sizeof(int));
cout << "Before count sort : " << endl;
print_array(array_src, array_length);
count_sort(array_src, array_dst, max_num_of_array_src, array_length);
cout << "After count sort : " << endl;
print_array(array_dst, array_length);
free(array_dst);
array_dst = NULL;
return 0;
}
int count_sort(int array_src[], int array_dst[], int max_num_k, int array_length)
{
int i = 0, j = 0;
int *p_count_array = (int *)malloc((max_num_k+1)*sizeof(int));
if(NULL == p_count_array)
{
cout << "p_count_array malloc error !" << endl;
return -1;
}
memset(p_count_array, 0 , (max_num_k+1)*sizeof(int));
for(j = 0; j < array_length; j++)
{
//p_count_array contain the numbers of items that equal to array[j]
p_count_array[array_src[j]] = p_count_array[array_src[j]] + 1;
}
for(i = 1; i <= max_num_k; i++)
{
//p_count_array contain the numbers of items that less and equal to i
p_count_array[i] = p_count_array[i] + p_count_array[i-1];
}
for(j = array_length-1; j >=0; j--)
{
//because numbers of items that less and equal to array_src[j] is p_count_array[array_src[j]],
//so we can confirm the position of array_src[j], locate array_src[j] to
//array_dst[p_count_array[array_src[j]] -1], and subtract p_count_array[array_src[j]], then
//the less or same items (if any) locate before witch. for example if array_src[j] = 3,
//and p_count_array[array_src[j]] is 2(mean less and equal to 3 exist 2 items), so we can
//locate 3 to position 2-1=1, the last less or equal items locate before it.
array_dst[p_count_array[array_src[j]]-1] = array_src[j];
p_count_array[array_src[j]] = p_count_array[array_src[j]] - 1;
}
free(p_count_array);
p_count_array = NULL;
return 0;
}
void print_array(int array[], int length)
{
int i = 0;
for(i=0; i<length; i++)
{
cout << array[i] << " ";
}
cout << endl << endl;
}
为了方便代码实现,本文下标从0下表开始,同算法导论书中表述略有出处。如有任何问题,欢迎各位指正。
因为统计计数对数据限制过多,要求最大数比总个数小,时间,空间复杂度才可控,所以实际项目中试用很少。
reference :
算法导论英文版第三版