数据结构-二叉搜索树(Binary Search Tree)的C++实现模板

    笔者最近开始学习了二叉树这种数据结构，于是写出了一个二叉树的实现~

    二叉树真是个好东西 =。=

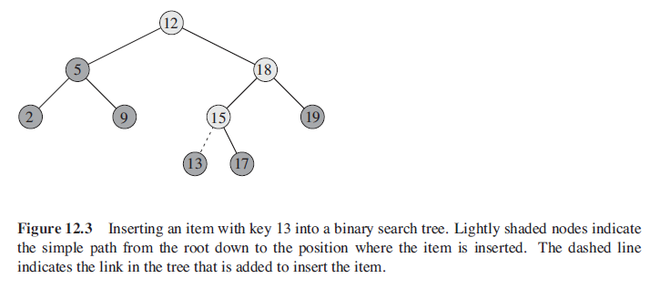
    该图显示了在二叉树中插入一个节点的步骤...下面就用这个二叉树做测试好了

/** "BST.h"
 * The Binary Search Tree Data Structure in C++
 * Time Cost : Inorder / Preorder / Postorder Traversal : O(n)
 *             Search / Find / Insert / Delete / Successor / Predecessor / Minimum / Maximum : O(h)
 *             Transplant : O(1)
 * Thanks to Introduction to Algorithms (CLRS) Chapter 12
 * Thanks to Stanford MOOC of "Algorithms : Part I"
 * Author: Zheng Chen / Arclabs001
 * Email : [email protected]
 * Copyright 2015 Xi'an University of Posts & Telecommunications. All rights reserved.
 */
#include <iostream>
#include <stack>
using namespace std;

struct TreeNode {
    int key;
    TreeNode *parent;
    TreeNode *left, *right;

    TreeNode& operator = (TreeNode& node)  //Reload the "=" for assignment
    {
        this->key = node.key;
        this->parent = node.parent;
        this->left = node.left;
        this->right = node.right;
        return *this;
    }

    bool operator < (TreeNode& node) const { return this->key < node.key;}
    bool operator > (TreeNode& node) const { return this->key > node.key;}
};

class Binary_Search_Tree
{
private:
    TreeNode * root;
    int _size;
    TreeNode * Tree_Minimum(TreeNode * x);  //Get the minimum key in x's posterity and return the pointer to that node
    TreeNode * Tree_Maximum(TreeNode * x);  //Get the maximum key in x's posterity and return the pointer to that node

public:
    void Tree_Insert(int _key);    //Insert a node valued "_key" to the tree
    Binary_Search_Tree() {root = nullptr; _size = 0;}   //Constructor

    void Inorder_Traversal();
    void Preorder_Traversal();
    void Postorder_Traversal();

    void Transplant(TreeNode * u, TreeNode * v);
    bool Tree_Delete(int _key);
    TreeNode * Find(int _key);
    TreeNode * Tree_Successor(TreeNode * x);
    TreeNode * Tree_Predecessor(TreeNode * x);

    TreeNode * Tree_getMinimum() { return Tree_Minimum(root);}
    TreeNode * Tree_getMaximum() { return Tree_Maximum(root);}
};

void Inorder_Tree_Walk(TreeNode * root)     //The recursion version of Inorder Traversal
{
    if(root != nullptr)
    {
        Inorder_Tree_Walk(root->left);
        cout<<root->key<<" ";
        Inorder_Tree_Walk(root->right);
    }
}

void Binary_Search_Tree::Inorder_Traversal(/*TreeNode * root */)    //The circulation version of Inorder Traversal
{
    cout<<"Inorder Traversal : ";
    stack<TreeNode *> TreeNode_Stack;
    TreeNode * p = root;

    while(p!=nullptr || !TreeNode_Stack.empty())
    {
        while(p!=nullptr)
        {
            TreeNode_Stack.push(p);
            p = p->left;
        }
        if(!TreeNode_Stack.empty())
        {
            p = TreeNode_Stack.top();
            TreeNode_Stack.pop();
            cout<<p->key<<" ";
            p = p->right;
        }
    }
    cout<<endl;
}

void Preorder_Tree_Walk(TreeNode * root)    //The recursion version of Preorder Traversal
{
    if(root != nullptr)
    {
        cout<<root->key<<" ";
        Preorder_Tree_Walk(root->left);
        Preorder_Tree_Walk(root->right);
    }
}

void Binary_Search_Tree::Preorder_Traversal(/*TreeNode * root */)   //The circulation version of Preorder Traversal
{
    cout<<"Preorder Traversal : ";
    stack<TreeNode *> TreeNode_Stack;
    TreeNode * p = root;

    while(p!=nullptr || !TreeNode_Stack.empty())
    {
        while(p!=nullptr)
        {
            TreeNode_Stack.push(p);
            cout<<p->key<<" ";
            p = p->left;
        }
        if(!TreeNode_Stack.empty())
        {
            p = TreeNode_Stack.top();
            TreeNode_Stack.pop();
            p = p->right;
        }
    }
    cout<<endl;
}

void Postorder_Tree_Walk(TreeNode * root)   //The recursion version of Postorder Traversal
{
    if(root != nullptr)
    {
        Postorder_Tree_Walk(root->left);
        Postorder_Tree_Walk(root->right);
        cout<<root->key<<" ";
    }
}

void Binary_Search_Tree::Postorder_Traversal(/*TreeNode * root */)  //The circulation version of Postorder Traversal
{
    cout<<"Postorder Traversal : ";
    int flag_visited[_size];
    stack<TreeNode *> TreeNode_Stack;
    TreeNode * p = root;

    while(p!=nullptr)
    {
        TreeNode_Stack.push(p);
        p = p->left;
        flag_visited[TreeNode_Stack.size()] = 0;
    }

    while(!TreeNode_Stack.empty())
    {
        p = TreeNode_Stack.top();
        while(p!=nullptr && p->left!=nullptr && flag_visited[(int)TreeNode_Stack.size()]==0)
        {
            flag_visited[(int)TreeNode_Stack.size()] = 1;
            p = p->right;
            while(p!=nullptr)
            {
                TreeNode_Stack.push(p);
                p = p->left;
                flag_visited[(int)TreeNode_Stack.size()] = 0;
            }
        }
        p = TreeNode_Stack.top();
        cout<<p->key<<" ";
        TreeNode_Stack.pop();
    }
    cout<<endl;
}

TreeNode * Tree_Search(TreeNode * root, int _key)   //The recursion version of Search a node valued key
{
    if(root==nullptr || root->key==_key)
    {
        return root;
    }
    else if(root->key > _key)
    {
        return Tree_Search(root->left, _key);
    }
    else
    {
        return Tree_Search(root->right, _key);
    }
}

TreeNode * Binary_Search_Tree::Find(/*TreeNode * root,*/ int _key)  //The circulation version of Search
{
    TreeNode * p = root;

    while(p != nullptr && p->key!=_key)
    {
        if(p->key > _key)
            p = p->left;
        else
            p = p->right;
    }
    return p;
}

//Get the minimum key in x's posterity and return the pointer to that node
TreeNode * Binary_Search_Tree::Tree_Minimum(TreeNode * root)
{
    TreeNode * p = root;

    while(p->left != nullptr)
    {
        p = p->left;
    }
    return p;
}

//Get the maximum key in x's posterity and return the pointer to that node
TreeNode * Binary_Search_Tree::Tree_Maximum(TreeNode * root)
{
    TreeNode * p = root;

    while(p->right != nullptr)
    {
        p = p->right;
    }
    return p;
}

TreeNode * Binary_Search_Tree::Tree_Successor(TreeNode * x)     //Find the successor in "Inorder Traversal Order"
{
    if(x->right!=nullptr)
    {
        return Tree_Minimum(x->right);
    }

    TreeNode * p = x->parent;
    while(p!=nullptr && x==p->right)
    {
        x = p; p = p->parent;
    }
    return p;
}

TreeNode * Binary_Search_Tree::Tree_Predecessor(TreeNode * x)   //Find the predecessor in "Inorder Traversal Order"
{
    if(x->left!=nullptr)
    {
        return Tree_Maximum(x->left);
    }

    TreeNode * p = x->parent;
    while(p!=nullptr && x==p->left)
    {
        x = p; p = p->parent;
    }
    return p;
}

void Binary_Search_Tree::Tree_Insert(int _key)      //Insert a node into the tree valued key
{
    TreeNode * z = new TreeNode;
    z->key = _key; z->left = z->right = nullptr;

    TreeNode * x = root;
    TreeNode * y = nullptr;

    while(x!=nullptr)   //Find the parent of the new node
    {
        y = x;
        if(z->key < x->key)
        {
            x = x->left;
        }
        else
        {
            x = x->right;
        }
    }
    z->parent = y;

    if(y==nullptr)  //When the tree is empty
        root = z;

    else if (z->key < y->key)
    {
        y->left = z;
    }
    else
    {
        y->right = z;
    }

    _size++;
}

//Replace the subTree rooted u with the subTree v
void Binary_Search_Tree::Transplant(TreeNode * u, TreeNode * v)
{
    if(u->parent == nullptr)
    {
        root = v;
    }
    else if(u == u->parent->left)
    {
        u->parent->left = v;
    }
    else
    {
        u->parent->right = v;
    }

    if(v != nullptr)
        v->parent = u->parent;
}

bool Binary_Search_Tree::Tree_Delete(int _key)    //Delete the node valued key
{
    TreeNode * z = Find(_key);
    if(z == nullptr)
    {
        cout<<"Error : No node valued "<<_key<<" !"<<endl;
        return false;
    }

    if(z->left == nullptr)
    {
        Transplant(z, z->right);
    }
    else if(z->right == nullptr)
    {
        Transplant(z, z->left);
    }
    else
    {
        TreeNode * y = Tree_Minimum(z->right);
        if(y->parent != z)
        {
            Transplant(y, y->right);
            y->right = z->right;
            y->right->parent = y;
        }
        Transplant(z, y);

        y->left = z->left;
        y->left->parent = y;
    }

    delete z;
    --_size;
    return true;
}

下面就测试这些接口了：

//"main.cpp"
#include "BST.h"
int _arr[] = {12,5,18,2,9,15,19,17};

int main()
{
    Binary_Search_Tree T;   //Test the Constructor
    for(int i=0; i<8; i++)
    {
        T.Tree_Insert(_arr[i]);    //Test the Insert function
    }

    T.Inorder_Traversal();    //Test the inorder traversal function
    T.Tree_Insert(13);
    T.Inorder_Traversal();

    TreeNode * tmp = T.Tree_Successor(T.Find(2));   //Test the Search and Successor function
    cout<<endl<<"The Node after "<<2<<" in the inorder traversal order is : "<<tmp->key<<endl;
    tmp = T.Tree_getMaximum();    //Test the maximum function
    cout<<"The largest node is : "<<tmp->key<<endl<<endl;
    T.Tree_Delete(9);   //Test the delete function

    T.Inorder_Traversal();      //Test the inorder traversal function
    T.Preorder_Traversal();     //Test the preorder traversal function
    T.Postorder_Traversal();    //Test the postorder traversal function

    cout<<endl;
    T.Tree_Delete(1);   //Test the delete function when there is no node valued "1".
    return 0;
}