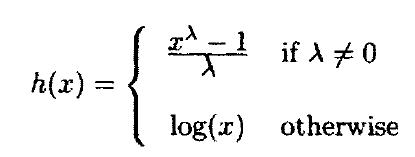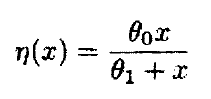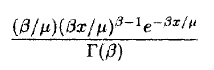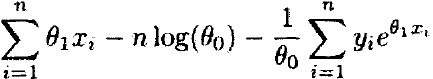Lisp-Stat 翻译 —— 第二章 Lisp-Stat教程
第二章 一份Lisp-Stat教程
本章打算将使用Lisp-Stat作为统计计算器和绘图器做一个介绍。在介绍完基本的数值和绘图操作之后,介绍如何构建随机的和系统的数据集合,如何修改数据集,如何使用一些内建的动态绘图工具,如何构建线性回归模型。最后两节给出了简略的介绍,关于如何写你自己的函数和使用功能数据进行高级建模的工具。
2.1 Lisp解释器
你与Lisp-Stat系统的交互是由你和lisp解释器之间的对话组成的。想象一下,你坐在计算机前打开了你的系统,或者更好点儿,你获取了某个版本的Lisp-Stat,并且启动了它。当准备好要开始对话时,Lisp-Stat在一个空白行的前边给出了一个提示符,就像这样:
>如果你键入一个表达式,解释器就会打印这个表达式的计算结果来响应你。例如,如果你给解释器一个数字,然后按回车键,那么解释器就会响应你——简单地 打印 这个数字,然后 在下一行 退出并给你一个新的提示符。
> 1 1对数字的操作可以通过组合数字和一个符号并把它们复合成一个表达式来执行,就像这样(+ 1 2):
> (+ 1 2) 3就像你猜想的一样,这个表达式就是将数字1和2加在一起。这种操作符放在操作数前边的表示方法叫前置表示法。这种表示方法起初可能让你很迷惑,因为它背离了标准的数学实践,但是却会带来一些很有意义的优势。一个优势是可以容纳进行任意数量的参数操作。例如,
> (+ 1 2 3) 6 > (* 2 3.7 8.2) 60.68为了理解解释器是如何工作的,要记住的一条基本的原则是所有的东西都是可以被求值的。数字求值得到它本身。
> 416 416 > 3.14 3.14 > -1 -1还有一些其它的基本数据形式求值后也会得到它本身。它们包括逻辑值
> t T > nil NIL还有字符串,它们将用双引号括起来。
> "This is a string 1 2 3 4" "This is a string 1 2 3 4"分号";"是Lisp注释符,任何在分号后键入的字符,直到你下次键入回车,其间的所有内容都会被解释器忽略。
如果解释器接收到一个符号(symbol,Lisp术语),像"pi"或者"this-is-a-symbol",来计算的话,它将首先检查是否有一个值与该符号关联,如果有值关联就返回那个值:
> pi 3.141593如果没有值与该符号关联,解释器将发出一个错误信号:
> x error: unbound variable - X符号pi是系统预定义的,作为数字π的一个近似值。从这点来看,符号x是没有值的。下一节我们将看到如何给一个符号赋值。
当你敲写符号名称时,可以用大写形式也可以用小写形式。Lisp内部会将小写字母转换为大写形式。
组合表达式的求值有一点点复杂。一个组合表达式是由一些放在小括号内部对的,用空格分开的元素的列表组成的。列表的元素可以是字符串、数字或者其它的组合表达式。在对形如(+ 1 2 3)这样的表达式求值时,解释器把这个列表当成一个函数表达式。列表的第一个元素代表一个Lisp函数——可以接受一些参数并且返回一个结果的代码段。本例中的函数式加法函数,由符号"+"表示,列表的其余元素是它的参数,这里是1、2和3。当要求对表达式求值时,解释器调用加法函数,把它应用到参数上,然后返回结果:
> (+ 1 2 3) 6函数的参数在函数使用之前已经被求值。在前边的例子里,参数都是数字,因此求值结果为自身。但是在下边这个例子里:
> (+ (* 2 3) 4) 10在加法函数使用之前,解释器不得不先对第一个参数(* 2 3)求值,再传递给加法函数。
数字、字符串和符号是一些在Lisp里可以直接使用的基本数据类型。我将会指出这些基本数据类型共同当做简单数据。还有,Lisp提供了一些方法来形成更复杂的数据结构,那些叫复合数据。最基本的复合数据就是列表——list。列表可以使用"list"函数来构造:
> (list 1 2 3 4) (1 2 3 4)解释器打印的这条结果很像我们已经用过的那个复合表达式:一个放在小括号里的,由空格分开的元素序列。事实上,Lisp表达式就是简单的列表。
一些其它复合数据形式也是可用的,包括矢量(vector)和多维数组。这些在4.4节再讨论。
在开始第一个统计应用程序之前,让我们再看一个解释器的特性。假设我们想要解释器打印一个列表(+ 1 2)给我们,直接把这个列表键入解释器是不行的,因为解释器会坚持对该列表求值:
> (+ 1 2) 3解决办法就是告诉解释器不要对列表求值。这个处理过程叫做引用(quoting)。就像这样,在一个手写的句子里,将一个表达式周围加上引号,然后说:把这个表达式当成字面意思理解。例如,使用引号标记下表这两个句子:Say your name! 和 Say "your name"!这两句话的意思是不同的。下表的表达方式告诉你如何在Lisp里引用表达式:
> (quote (+ 1 2)) (+ 1 2)"quote"不是一个函数,它不遵守上边描述的函数求值规则:它的参数不会被求值。"quote"可以被称为一个special form——特殊是因为在处理参数上它有特殊的规则。需要的时候我还会介绍其他的special forms。这些基本求值规则与这些special forms(特殊形式)一起组成了Lisp语言的语法。
"quote"使用频率如此之高以至于专门开发了一个速记符,就是标记在表达式之前的单引号:
> '(+ 1 2) ;单引号速记符 (+ 1 2)也就是说,上边的表达式与(quote (+ 1 2))是相同的。
一旦你学会如何启动一个计算机程序,确保指导如何退出程序是个好主意。在大多数Lisp系统里你可以通过使用exit函数退出。在提供%的shell提示符的UNIX操作系统里,使用exit函数应该会返回shell:
> (exit) %其它操作系统可能会提供额外的退出方式。例如,在Macintosh操作系统里,你可以到“文件”菜单里选择“退出”选项退出。
练习 2.1
先预测,再上机实验。
a) (+ 3 5 6)
b) (+ (- 1 2) 3)
c) '(+ 3 5 6)
d) (+ (- (* 2 3) (/ 6 2)) 7)
e) 'x
f) ''x
2.2 初级计算与绘图
本节介绍一些在Lisp-Stat里可用的基本的数值与绘图操作。
2.2.1 一维概要与图形
统计数据经常是由数字组组成的。作为一个例子,下表展示了Minnea-St地区30年间3月份降水量数据记录,单位为英寸。
为了在Lisp-Stat里检测这些数据,我们可以list函数将数据重新显示为数字列表,表达式如下:
> (list .77 1.74 .81 1.20 1.95 1.20 .47 1.43 3.37 2.20
3.00 3.09 1.51 2.10 .52 1.62 1.31 .32 .59 .81
2.81 1.87 1.18 1.35 4.75 2.48 .96 1.89 .90 2.05)
这些数字必须用空格分开,不是逗号。解释器允许你跨多行表示数据,它不会求值直到你完成表达式的书写并键入回车为止。
"mean"函数可用来计算数字列表的平均值。我们可以用它和list函数组合在一起,来求取降水量样本数据的平均值:
> (mean (list .77 1.74 .81 1.20 1.95 1.20 .47 1.43 3.37 2.20
3.00 3.09 1.51 2.10 .52 1.62 1.31 .32 .59 .81
2.81 1.87 1.18 1.35 4.75 2.48 .96 1.89 .90 2.05))
1.675 降水量的中位数可以这么计算:
> (median (list .77 1.74 .81 1.20 1.95 1.20 .47 1.43 3.37 2.20
3.00 3.09 1.51 2.10 .52 1.62 1.31 .32 .59 .81
2.81 1.87 1.18 1.35 4.75 2.48 .96 1.89 .90 2.05))
1.47
每次我们想对数据样本进行统计计算的时候,都不得不敲入30组数字,这当然是一件令人恼火的事情。为了避免做那要的工作,我们可以Lisp-Stat的一个特殊形式"def"来给数据列表一个变量名。
> (def precipitation
(list .77 1.74 .81 1.20 1.95 1.20 .47 1.43 3.37 2.20
3.00 3.09 1.51 2.10 .52 1.62 1.31 .32 .59 .81
2.81 1.87 1.18 1.35 4.75 2.48 .96 1.89 .90 2.05))
PRECIPITATION 现在,符号precipitation有一个值与它绑定了,我们的30个数字的列表可以这样获得:
> precipitation (.77 1.74 .81 1.20 1.95 1.20 .47 1.43 3.37 ...)现在,我们再对这些数据记性各种数值描述性统计及容易得多了:
> (mean precipitation) 1.675 > (median precipitation) 1.47 > (standard-deviation precipitation) 1.00062 > (interquartile-range precipitation) 1.145
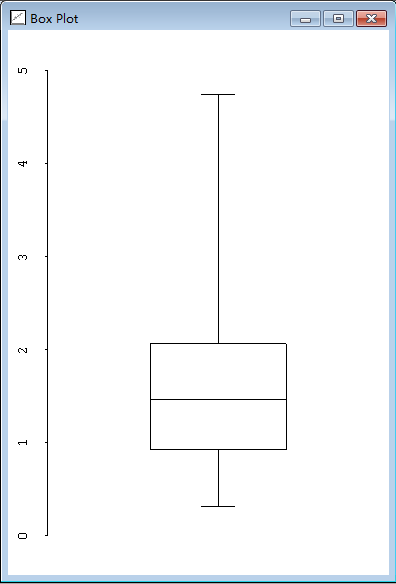
函数histogram和boxplot可以用来获得样本数据的图形化展示,见图2.1和图2.2。
> (histogram precipitation) #<Object: 143cd68, prototype = HISTOGRAM-PROTO> > (boxplot precipitation) #<Object: 145ef04, prototype = SCATTERPLOT-PROTO>
图2.1 数据柱状图
图2.2 数据盒图
这两个表达式是会将绘图窗口显示在显示器上。这两个函数返回两条类似这样的信息:#<Object: 143cd68, prototype = HISTOGRAM-PROTO>这个结果之后会被用来识别包含图形的窗口,但这会儿你可以忽略它。
Lisp-Stat也支持数字列表数据的对应元素相乘操作(点乘)。例如,我们可以在降水量数据的每个元素上加1:
> (+ 1 precipitation) (1.77 2.74 1.81 2.2 2.95 2.2 1.47 2.4299999999999997 4.37 3.2 4.0 4.09 2.51 3.1 1.52 2.62 2.31 1.32 1.5899999999999999 1.81 3.81 2.87 2.1799999999999997 2.35 5.75 3.48 1.96 2.8899999999999997 1.9 3.05)或者计算它们的自然对数,
> (log precipitation) (-0.2613647641344075 0.5538851132264376 -0.21072103131565253 0.1823215567939546 0.6678293725756554 0.1823215567939546 -0.7550225842780328 0.3576744442718159 1.2149127443642704 0.7884573603642703 1.0986122886681098 1.128171090909654 0.412109650826833 0.7419373447293773 -0.6539264674066639 0.4824261492442928 0.2700271372130602 -1.1394342831883648 -0.527632742082372 -0.21072103131565253 1.0331844833456545 0.6259384308664954 0.16551443847757333 0.30010459245033816 1.55814461804655 0.9082585601768908 -0.040821994520255166 0.636576829071551 -0.10536051565782628 0.7178397931503168)或者平方根:
(sqrt precipitation) (0.8774964387392122 1.3190905958272918 0.9 1.0954451150103321 1.396424004376894 1.0954451150103321 0.6855654600401044 1.1958260743101399 1.835755975068582 1.4832396974191326 1.7320508075688772 1.7578395831246945 1.2288205727444508 1.449137674618944 0.7211102550927979 1.2727922061357855 1.1445523142259597 0.565685424949238 0.7681145747868608 0.9 1.676305461424021 1.3674794331177345 1.0862780491200215 1.161895003862225 2.179449471770337 1.5748015748023623 0.9797958971132712 1.374772708486752 0.9486832980505138 1.4317821063276353)降水量数据的分布有些右偏,平均值和中位数是分离的。你可能想要试着做一些简单的变换来看看能否对称化数据,比如说平方根或者对数。你可以查看图形和概要统计来确定是否这些变换确实导致数据更加对称化一些。例如,可以用下边的表达式计算数据样本的平方根的均值:
> (mean (sqrt precipitation)) 1.2401878297708169也可以获得样本数据的平方根的柱状图:
> (histogram (sqrt precipitation))boxplot函数还能用来并列地产生两个或者更多的数据样本。只需要传递给boxplot函数列表型参数,这个列表型参数是由多个列表数据组成的,其中的每条列表数据都是要显示在统计图形串口上的数据样本。让我们用这个函数测试一些数据样本,这些数据来源于危地马拉的一些社会经济学团体对血液化学的研究。高收入的城市区域和低收入的乡村区域样本的血清总胆固醇数据,可以用下边的表达式输入:
> (def urban (list 206 170 155 155 134 239 234 228 330 284
201 241 179 244 200 205 279 227 197 242))
URBAN
> (def rural (list 108 152 129 146 174 194 152 223 231 131
142 173 155 220 172 148 143 158 108 136))
RURAL 并列的盒图可以用以下表达式表示:
> (boxplot (list urban rural))
结果见图2.3。
图2.3 危地马拉城市与乡村总胆固醇水平并列盒图
练习 2.2先预测,后实践,并解释其间的不同。
a) (mean (list 1 2 3))
b) (+ (list 1 2 3) 4)
c) (* (list 1 2 3) (list 4 5 6))
d) (+ (list 1 2 3) (list 4 5))
练习 2.3
略。
练习 2.4
略。
2.2.2 二维绘图
很多单一样本是随着时间的推移收集的。上面用到的降水量数据就是一个例子。在一些情况下假设观测数据之间相互独立式合理的,但在有的情况下是不合理的。检查数据以获得序列相关性和趋势的一种方式,就是绘制观测数据相对于时间,或者相对于数据自身顺序的图形。我们可以使用plot-points函数来产生一幅降水量数据相对于时间的散点图。plot-points函数使用下边的表达式形式调用:(plot-points <x-variable> <y-variable>)。其中,<y-variable>可以是precipitation,就是我们以前定义的变量;<x-variable>我们可以使用从1到30的自然数序列,我们可以自己手动输入,但有一个更简单的办法,使用函数integer-sequence的简写形式iseq来生成两个指定值之间的连续自然数列表。调用iseq函数的一般形式是这样的: (iseq <start> <end>)。为了生成我们需要的序列,我们使用:
> (iseq 1 30)那么为了生成散点图,我们需要键入以下表达式:
> (plot-points (iseq 1 30) precipitation)结果见图2.4。对数据来说,本图似乎过多的形式,独立性的假设对该数据来说可能是合理的。
图2.4 降水量水平相对于时间的散点图
有时用线将点连接起来,就很容易在图形里看到时间形式。使用plot-lines函数可以构造一个连接点数据的连接线。plot-lines也可以被用来构造函数的曲线图。假设你想得到自变量在-π到+π范围内的sin(x)函数的图形,其中常量π由变量pi预定义,你可以使用这个表达式:(rseq <a> <b> <n>)来构建数字a与b之间的n等间隔实数。那么为了绘制间隔数为50的等间隔点的sin(x)函数的图像,可以这样:
> (plot-lines (rseq (- pi) pi 50) (sin (rseq (- pi) pi 50)))你也可以先定义一个变量x来简化这个表达式,
> (def x (rseq (- pi) pi 50)然后重新构造表达式:
> (plot-lines x (sin x))最终图形见图2.5。
图2.5 sin(x)图形
散点图在检测两组数值观测量之间的关系上,当然是非常有用的,这两组观测量是针对同一目标的。一项针对机动车尾气排放过程的研究给出了46两汽车的HC和CO排放数据,结果放在两个变量hc和co里:
> (def hc (list .50 .65 .46 .41 .41 .39 .44 .55 .72 .64 .83 .38
.38 .50 .60 .73 .83 .57 .34 .41 .37 1.02 .87 1.10
.65 .43 .48 .41 .51 .41 .47 .52 .56 .70 .51 .52
.57 .51 .36 .48 .52 .61 .58 .46 .47 .55))
> (def co (list 5.01 14.67 8.60 4.42 4.95 7.24 7.51 12.30
14.59 7.98 11.53 4.10 5.21 12.10 9.62 14.97
15.13 5.04 3.95 3.38 4.12 23.53 19.00 22.92
11.20 3.81 3.45 1.85 4.10 2.26 4.74 4.29
5.36 14.83 5.69 6.35 6.02 5.79 2.03 4.62
6.78 8.43 6.02 3.99 5.22 7.47))
然后,可以用plot-points函数将它们一一对应地绘制到一幅图里:
> (plot-points hc co)结果见图2.6。
图2.6 机动车尾气排放的CO相对HC图形
练习2.6
略。
2.2.3 绘图函数
上一节中,正弦函数的制图函数显得非常笨重。作为一个代替品,我们可以使用plot-function来绘制有一个参数的函数,该参数有一个指定的范围。为了产生图2.5中的图形,我们可以使用表达式:
> (plot-function (function sin) (- pi) pi)表达式(function sin)用来提取与符号sin相关联的Lisp函数,仅仅使用sin还不够,原因是Lisp里的符号可能是由def设定的数值,同时也可能是一个函数定义。起初这一特性看起来有些奇怪,但是它也有一个很大的优势——键入一个像这样的合法表达式:
> (def list '(2 3 4))而不会销毁list函数。
从一个符号里提取一个函数定义就像引用表达式一样常见。所以又有一个新的可用的缩写符号,表达式#'sin和表达式(function sin)是等价的(注:这点与Common Lisp里相似,有兴趣的朋友可以参考Common Lisp里的function和apply的用法)。#'的读音是sharp-quote。使用这个缩写,产生正弦图形的表达式可以写成这样:
> (plot-function #'sin (- pi) pi)
2.3 进一步了解解释器
Lisp-Stat解释器允许保存创建的变量,可以部分或全部地记录与解释器的会话。另外,它还提供了获得最近几条计算结果的机制,还有获得在线帮助的机制。这几个特性可能根据所运行的系统的不同稍微有些差异,尤其是在线帮助系统,例如,一些系统可能提供了单独的帮助窗口。我的相关工作是基于XLIST-STAT这一实现版本的。
2.3.1 保存你的工作
如果你想要与解释器的一个会话,你可以使用dribble函数。表达式
> (dribble "myfile")将开始一个记录。所有你输入的表达式和解释器返回的结果都会输入到这个叫myfile的文件,表达式
> (dribble)会停止录制工作。表达式(dribble "myfile")通常会开始一个名称为myfile的新文件,如果你已经有了这个名字的文件,其内容将全部丢失。因此你不能用dribble函数对单个文件进行开启和关闭。
dribble仅会记录文本,不会记录图形。Macintosh的XLISP-STAT里你能使用标准Macintosh快捷命令COMMAND-SHIFT-3来保存当前屏幕的图像。也可以到Edit菜单里选择Copy命令,或者其快捷键COMMAND-C,图形窗口是一个活动窗口,用来将内容保存到剪切板。在X11版的XLISP-STAT,绘图菜单包含一个选项,该选项可以将图形的PostScript版本保存成文件。
你在Lisp-Stat里定义的变量只能存在于当前会话,如果你从Lisp-Stat里退出,或者程序崩溃了,你的数据就会丢失。为了保存你的数据可以使用savevar函数。这个函数允许你将一个或多个变量保存到一个文件里。新文件创建时,任何同名文件都会被销毁。为了将变量precipitation保存到一个名为precipitation.lsp的文件,键入:
> (savevar 'precipitation "precipitation")不需要加.lsp后缀名,savevar会帮你加上的。为了保存两个变量hc和co到examples.lsp文件,键入:
(savevar '(hc co) "samples")我使用一个带引号的列表'(hc co)并将该符号列表传递给savevar函数。还有一个长点的表达式可以代替它:(list 'hc 'co)。
文件precipitation.lsp和samples.lsp获得了表达式集合,当使用read函数读取这两个文件的时候,它们将重新创建precipitation、hc和co变量。为了加载precipitation.lsp文件,可以使用如下表达式:
> (load "precipitation")
2.3.2 命令历史机制
Common Lisp提供了一个简单的命令历史机制。符号 -, *, **, ***, +, ++和+++就是为实现这一意图的。解释器将这些符号与其意义绑定如下:
- - 当前输入的表达式
- + 读取最近一个表达式
- ++ +返回的表达式的前一个表达式
- +++ ++返回的表达式的前一个表达式
- * 最近的一个表达式的结果
- ** *所属表达式的前一个表达式的结果
- *** **所属表达式的前一个表达式的结果
*, **, ***这三个变量也许是最有用的。例如,如果你想求某个变量的对数值,但忘了给它定义变量名,你就可以使用那几个历史变量来避免重复计算对数:
> (log precipitation) (-0.2613647641344075 0.5538851132264376 -0.21072103131565253 0.1823215567939546 0.6678293725756554 0.1823215567939546 -0.7550225842780328 0.3576744442718159 1.2149127443642704 0.7884573603642703 1.0986122886681098 1.128171090909654 0.412109650826833 0.7419373447293773 -0.6539264674066639 0.4824261492442928 0.2700271372130602 -1.1394342831883648 -0.527632742082372 -0.21072103131565253 1.0331844833456545 0.6259384308664954 0.16551443847757333 0.30010459245033816 1.55814461804655 0.9082585601768908 -0.040821994520255166 0.636576829071551 -0.10536051565782628 0.7178397931503168) > (def log-precip *)现在,变量log-precip就包含降水量数值的对数了。
系统利用了2.2.3节讨论的一个事实,那就是符号可以同时又函数定义和数值。符号*的函数定义是乘法函数,它的值是解释器返回的上一个求值结果。
2.3.3 获取帮助
Lisp-Stat提供了大量的不同的函数。我们不可能精确地记起每个函数的用法。一个交互式的帮助应用可以完成一些任务:找出需要的正确的函数,找出如何更容易地使用这个函数。例如,下边就是如何获得median函数帮助的例子:
> (help 'median) loading in help file information - this will take a minute ...done MEDIAN [function-doc] Args: (x) Returns the median of the elements of X. NIL >median函数前面的引号是必要的。help函数本身也是函数,它的参数是median函数的符号形式。为了确保help函数能够接受到符号,而不是符号的值,你需要引用(quote)这个符号(symbol)。
如果你对函数的名字不确定,你可能需要使用help*函数来获取帮助。假设你想找出与正太分布相关的函数,它们的名字里多数都包含"norm",表达式(help* 'norm)将打印函数名里包含"norm"的所有符号的帮助信息:
(help* 'norm) ------------------------------------------------------------------------------ BIVNORM-CDF [function-doc] Args: (x y r) Returns the value of the standard bivariate normal distribution function with correlation R at (X, Y). Vectorized. ------------------------------------------------------------------------------ Sorry, no help available on NORM ------------------------------------------------------------------------------ Sorry, no help available on NORMAL ------------------------------------------------------------------------------ NORMAL-CDF [function-doc] Args: (x) Returns the value of the standard normal distribution function at X. Vectorized. ------------------------------------------------------------------------------ NORMAL-DENS [function-doc] Args: (x) Returns the density at X of the standard normal distribution. Vectorized. ------------------------------------------------------------------------------ NORMAL-QUANT [function-doc] Args (p) Returns the P-th quantile of the standard normal distribution. Vectorized. ------------------------------------------------------------------------------ NORMAL-RAND [function-doc] Args: (n) Returns a list of N standard normal random numbers. Vectorized. ------------------------------------------------------------------------------ Sorry, no help available on NORMALREG-MODEL ------------------------------------------------------------------------------ Sorry, no help available on NORMALREG-PROTO ------------------------------------------------------------------------------ NIL >符号norm, normal, normalreg-model和normalreg-proto没有函数定义,因此没有可用的帮助信息。函数文档里的术语vectorized意味着这个函数可以被应用到形式为列表的参数上;它的结果是这个函数作用到参数的每一个元素后返回的结果列表。文档中出现的一个相关的术语是vector reducing。如果一个函数可以递归地操作它的参数,直到只剩一个单独的数字为止,那么这个函数就是vector reducing(矢量减少)的。函数sum, prod, max和min都是矢量减少的。
作为使用help*的替代品,你可以使用apropos函数来获得包含字符串"norm"作为其名字一部分的那些符号的列表:
> (apropos 'norm) NORMALREG-PROTO NORMALREG-MODEL NORM BIVNORM-CDF NORMAL-QUANT NORMAL-RAND NORMAL NORMAL-CDF NORMAL-DENS >然后使用help函数询问每个符号的更多信息。
让我来简要地介绍一下help函数打印的信息所用到的表示方法,来描述一个函数期望参数有的功能。表示方法对应的Lisp函数定义的参数列表的规格将在4.2节描述。多数函数期望参数列表是固定的,想在帮助信息里的这行一样: Args: (x y z)。有的参数可能会接收一个或多个可选参数,这种函数的参数可能会这样表示: Args: (x &optional y (z t)),这意味着x是必选参数,y和z是可选参数。如果这个函数命名是f,可以这样调用:(f x-val), (f x-val y-val),或者(f x-val y-val z-val)。列表(z t)意味着没有提供参数z,那它的默认值就是t;y是没有强制指定默认值的参数,因此它的默认值是nil。实参必须按照形参规定的顺序和规则来提供,因此如果你要是想传递参数z,那就必须先对y赋值。
另一个形式的可选参数是关键字参数。例如,histogram函数的参数是这样的:Args: (data &key (title "Histogram")),data参数是必选的,title就是可选的关键字参数,其默认值是"Histogram"。如果你用2.2.1节用到的降水量数据创建一张表,它的名字是"Precipitation"可以用这个表达式:
> (histogram precipition :title "Prcipitation")
图2.7 图形title修改示意图
因此,为了给关键字参数一个值,你将需要显式地给出这个关键字名,也就是一个由冒号紧跟着参数名的一个符号,然后是这个参数的值。如果一个函数带多个关键字参数,在调用时这些关键字参数之间的顺序可以任意指定,前提是他们需呀在必选参数可可选函数之后。(注:关于这点建议参考《实用Common Lisp编程》第4.2~4.5节,认真实践,方可领悟!)
最后,一些函数可能带不定数量的参数,可用下式表示:Args: (x &rest ars)。该参数列表表示参数x是必选参数,同时可以带0个到多个附加参数。(注:相当于C语言参数列表里的 “...”)
除了函数,help函数还能针对数据类型和一些变量给出帮助信息。例如:
> (help 'complex) loading in help file information - this will take a minute ...done COMPLEX [function-doc] Args: (realpart &optional (imagpart 0)) Returns a complex number with the given real and imaginary parts. COMPLEX [type-doc] A complex number NIL这个例子展示了complex复数数据类型的功能和类型信息。下边这个例子
> (help 'pi) PI [variable-doc] The floating-point number that is approximately equal to the ratio of the circumference of a circle to its diameter. NIL展示了pi这个变量的文档。
2.3.4 列举变量和取消变量定义
在工作一段时间之后,你可能想要查明使用def宏定义了哪些变量,variables函数将以列表的方式返回这些变量:
> (variables) (CO HC PRECIPITATION RURAL URBAN)你可能偶尔对不在使用的变量进行释放以获得一些空间。要达到这个目的你可以使用undef函数:
> (undef 'co) CO > (variables) (HC PreCIPITATION RURAL URBAN)undef的参数是一个符号(symbol),本例总我们必须引用它以避免解释器对其求值。undef也能接受符号列表当做参数,因此想要取消定义当前所有已经定义的变量,可以这样:
> (undef (variables)) (HC PRECIPITATION RURAL URBAN) > (variables) NIL
2.3.5 中断计算
偶尔你可能在系统里开始了这样一种计算,它耗用了太长的时间或者产生了一个看起来不合理的结果。每个系统都提供了一个机制来中断这样的计算过程,但是这些机制依据系统的不同而不同。在Macintosh操作系统下的XLISP-STAT里,你可以按住COMMON键和PERIOD键直到系统将解释器交由你来输入。在UNIX版本的XLISP-STAT里,你可以按下为你的系统准备的中断键组合来中断这种计算,通常这个中断键组合为CONTROL+C。
2.4 一些数据处理函数
目前为止我们都是将数据直接敲到解释器里的,数据集较小,所以这也不是什么大问题,然而,有其它的替代方法会更有用。Lisp-Stat提供了一些函数,可以生成系统的数据和随机数据,可以提取数据集的一部分,修改数据集,并且可以从文件中读取数据。
2.4.1 生成有系统的数据
函数iseq用来生成连续的整数序列,rseq用来生成等间隔的实数序列,它们在2.2.2节提到了。函数iseq也可以通过传递一个单独参数来调用,这种情况下参数应该是一个正整数n,结果是从0到n-1的整数列表。例如:
> (iseq 10) (0 1 2 3 4 5 6 7 8 9)函数repeat在生成具有一定格式的序列时是很有用的,调用repeat函数的一般格式是(repeat <vals> <pattern>),参数<vals>可能是简单的数据项或者数据项列表,参数<pattern>必须是一个单独的正整数或者一组正整数列表。如果<pattern>是一个单独的正整数,repeat就会将<vals>重复<pattern>次,例如:
> (repeat 2 3) (2 2 2) > (repeat (list 1 2 3) 2) (1 2 3 1 2 3)如果<pattern>是一个列表,那么<vals>应该是一个与<pattern>相同长度的列表,本例中,<vals>和<pattern>两个列表中相同位置的元素市一一对应的,<pattern>中每个元素的值对应<vals>列表中相对元素重复的次数。例如:
> (repeat (list 1 2 3) (list 3 2 1)) (1 1 1 2 2 3)
函数repeat在设计实验中的编码处理层面上是极其有用的。例如,在一个测试植物种植密度对马铃薯生长的影响的实验里,有3个品种的马铃薯,种植在4个不同种植密度的地方,每一种测试组合重复3次,结果在下表中:
我们可以将这些数据按行,输入到产量变量里,如:
> (def yield (list 9.2 12.4 5.0 8.9 9.2 6.0 16.3 15.2 9.4
12.4 14.5 8.6 12.7 14.0 12.3 18.2 18.0 16.9
12.9 16.4 12.1 14.6 16.0 14.7 20.8 20.6 18.7
10.9 14.3 9.2 12.6 13.0 13.0 18.3 16.0 13.0)) 使用repeat,我们可以这样生成表示不同品种和密度水平的变量:
> (def variety (repeat (repeat (list 1 2 3) (list 3 3 3)) 4)) VARIETY > (def density (repeat (list 1 2 3 4) (list 9 9 9 9))) DENSITY >练习2.7
略。
练习2.8
略。
2.4.2 生成随机数据
一些函数可以生成伪随机数字,例如,表达式(uniform-random 50)将生成一个的数字列表,列表的元素是50个在0和1之间的独立随机均匀分布的数字。函数normal-rand和cauchy-rand也类似地生成标准正态的或标准柯西随机变量。表达式:
> (gamma-rand 50 4) (1.65463390351748 2.8773826027572174 3.324805876512575 3.7107737590852885 2.5322960063057325 2.3917079623070143 2.5738732854681405 5.114579884756656 4.503560922291987 3.8212691381896735 4.748609795710945 2.460930129538628 5.1583129719078125 2.8722892003673204 2.271632493827859 1.306689218830528 2.956587212984247 2.254496336799741 1.5432493948171886 1.0074517838362944 2.3221187903990685 2.9297357635208368 1.9111207190664348 4.086600231358658 8.498775494298609 3.309145002227253 8.43403656671126 2.9001355594385445 2.156028887326921 5.457111466807575 2.7180957670090233 6.727592025517272 3.2182935800579466 4.759355290676398 2.1463912302657 4.641326968027183 4.951716760175214 2.9685374305637593 5.934043534710339 6.847560103820065 5.612014958257557 4.4811213649680814 7.4465265497488975 2.6911820555097306 1.0087771420430949 1.4549088997831112 5.276729335543616 2.773807551655783 3.565519147704477 2.7611738530317305)
生成一个大小为50的数据样本,这些数据符合伽马-分布,单位尺度,指数为4。
指数为3.5~7.2的β分布变量可以这样生成:
> (beta-rand 50 3.5 7.2) (0.4565276604553964 0.2784641511528651 0.1992946182796908 0.15531331094658482 0.1524256312642991 0.26070619189857414 0.26797467262440017 0.22086809762954612 0.30818508575346343 0.31431320706862537 0.4767943879658169 0.3103165584027092 0.3099168733453603 0.48844354838756315 0.3850748530401529 0.5261394345014925 0.4729101627118159 0.34008228819566094 0.34728211784541685 0.11375668596438508 0.3177405260351405 0.15233790451255871 0.3247481923221466 0.16163693218582695 0.34148249992894264 0.26747115750175693 0.1917463536194362 0.3096184276126184 0.2815407126874605 0.27277307887112906 0.5364074613555034 0.5343432853990229 0.7113134763751001 0.2008014529296493 0.1610644249288089 0.14281693672275156 0.1994676889199915 0.3627351688059498 0.4983412412275205 0.4279902846854145 0.42865178072445864 0.32624949341033294 0.38525682966664915 0.3395031181658098 0.35242269440634416 0.3010577148339438 0.3497046925914022 0.12251980989006983 0.3635843569985974 0.12912742911247255)大小为50,自由度为4的t-分布随机变量样本:
> (t-rand 50 4)自由度为4的卡方-分布随机变量的生成表达式:
> (chisq-rand 50 4)分子自由度为3,分母自由度为12的F-分布的随机变量的生成表达式:
> (f-rand 50 3 12)参数n=5,p=0.3的二项式分布样本生成表达式为:
> (binomial-rand 50 5 .3)大小为50,期望值λ=4.3的泊松-分布随机数据样本生成表达式:
> (poisson-rand 50 4.3)这些样本生成函数的“大小”这一参数也可以是一个整数列表,相应地,返回的结果是样本列表的列表(即多条样本列表)。例如:
> (normal-rand (list 10 10 10)) ((0.24711492524397788 -0.08672761627290786 -0.3586542916304954 -1.2370666723700587 0.4973152707135397 1.2779437429528906 0.5433681505645361 -0.15811161781047764 -2.444951338731246 1.4391452075883056) (-0.024198159865474137 0.018494098689563702 -1.201497046490873 0.29215227642978814 -0.1504967544867967 0.8539957140604427 0.1866809359842353 -0.3235190277039044 1.2316501558225053 -0.3173822473522208) (2.6816999640212815 1.312819856883247 0.3381892163767421 0.20384488399908143 0.9360472535774436 -1.3160001465807794 0.033750173542764696 -0.4613961332004225 -0.9523674256520025 -2.2724093805908905))该表达式产生了一个列表集,其中的每个列表都是有十个正态分布变量的列表。
最后,你可以使用sample函数从一个列表里随机里选出一个数据样本,表达式(sample (iseq 1 20) 5)的返回值就是,在1, 2, ..., 20这个列表里,随机地选择5个元素,组成一个大小是5的新的没有重复元素的样本,其结果可能是:
> (sample (iseq 1 20) 5) (2 19 1 3 5)sample函数可以通过启用第三个参数(一个可选参数)来指定采样元素是否可以重复。那么下个表达式
> (sample (iseq 1 20) 5 t) (11 11 5 4 16)将允许sample函数在采样的时候允许元素重复(注:原文使用replacement表示的,但我无法翻译成合适的中文,如果有更精确的翻译,欢迎指正)。
第三个参数为nil时,sample函数采样时不允许元素重复,这与忽略这个参数的情况是一样的。
练习2.9
略。
2.4.3 建立子集和删除
select函数允许你从一个列表里选择一个单独的元素或者一组元素。例如,你这样定义了一个x变量:
> (def x (list 3 7 5 9 12 3 14 2))那么
> (select x i)将返回变量x的第i个元素。Lisp语言列表的下标是从0开始的,这点与C语言相同,但是和FORTRAN不同。因此它的下标应该是0, 1, 2, 3, 4, 5, 6, 7,所以有:
> (select x 0) 3 > (select x 2) 5为了获取一组元素,我们可以使用下标数组来代替单个的下标,即:
> (select x (list 0 2)) (3 5)如果你想选择除了下标为2的元素之外的所有元素的话,使用以下表达式
> (remove 2 (iseq 8))来产生下标序列,并把它作为select函数的第二个参数:
> (select x (remove 2 (iseq 8))) (3 7 9 12 3 14 2)表达式(iseq 8)生成了从0到7的整数列表。remove函数会返回一个移除指定元素的列表,那么
> (remove 3 (list 1 3 4 3 2 5)) (1 4 2 5)剩下的元素按它们在原始列表里的顺序返回。
另一个返回除了2号下标元素的方法是使用对照函数"/="(意思是“不等于”)来告诉你哪些下标不等于2:
> (/= 2 (iseq 8)) (T T NIL T T T T T)函数which能够返回,其函数的参数的不是nil的哪些下标的元素的列表,即
> (which (/= 2 (iseq 8))) (0 1 3 4 5 6 7)结果可以传递给select函数:
> (select x (which (/= 2 (iseq 8)))) (3 7 9 12 3 14 2)对于删除一个元素来说,这个方法有一点太笨重了,然而它却是一个通用的方法。例如如下表达式
> (select x (which (< 3 x))) (5 7 9 12 14)将返回所有比3大的元素。
由于我们在上边几个例子里用到的x变量比较短,通过数数我们也可以很容易地确定他的长度。对于再长点儿的列表就不太容易了,我们可以使用length函数来实现。使用length函数,我们也能实现"选择除了下边为2的其它元素"这一功能:
> (select x (remove 2 (iseq (length x))))练习2.10
略。
2.4.4 合并列表
有时你可能想将几个短的列表合并为一个长的列表,可以用append和combine函数来完成。例如,
> (append (list 1 2 3) (list 4) (list 5 6 7 8)) (1 2 3 4 5 6 7 8)或者
> (combine (list 1 2 3) (list 4) (list 5 6 7 8)) (1 2 3 4 5 6 7 8)这两个函数的不同在于它们对列表的列表的处理方式上。append函数只合并外部列表,而combine函数会递归地调用到子列表,并返回一个没有复合元素的列表(即不包含子列表):
> (append (list (list 1 2) 3) (list 4 5)) ((1 2) 3 4 5) > (combine (list (list 1 2) 3) (list 4 5)) (1 2 3 4 5)combine函数允许他的参数是数字或者其它简单数据项,比如:
> (combine 1 2 (list 3 4)) (1 2 3 4)而append函数的参数必须是列表(list)形式,否则会报错。
> (append 1 2 (list 3 4)) Error: bad argument type - 1 Happened in: #<Subr-APPEND: #14644cc>
2.4.5 修改数据
setf可以用来修改列表的单个元素或者列表的元素集合。再一次假设我们设置了一个列表x:
> (def x (list 3 7 5 9 12 3 14 2))我们想把12改成11,使用如下表达式(setf (select x 4) 11)来做这个替换:
> (setf (select x 4) 11) 11 > x (3 7 5 9 11 3 14 2)setf的一般形式为(setf <form> <value>),这里<form>是你想改变的列表里的那个元素或元素组,<value>是你想要改变成的那个值或多个值得列表。那么表达式(setf (select x (list 0 2)) (list 15 16))将下标为0和2的元素的值改成15和16,即:
> (setf (select x (list 0 2)) (list 15 16)) (15 16) > x (15 7 16 9 11 3 14 2)这里需要有一个小提示,Lisp符号只不过是不同项的标签而已,当我们使用def命令为一个项分配名字时,我们并没有产生一个新项,因此,表达式(def x (list 1 2 3 4))求值之后,在进行(def y x),符号x和符号y是针对相同列表的两个不同的名字。结果,我们使用setf对x的元素进行操作时,我们同时也改变了y的值,因为x和y在引用一个相同的列表。如果你想做一份x的拷贝,并且在x改变之前将之保存到y里,那么需要你强制执行,此时需要使用copy-list函数。表达式(def y (copy-list x))制作了x的一份拷贝,并将它设置给y变量。现在x与一引用了不同的项,改变x将不会影响到y的值。
setf也可以用来将一个值分配给一个符号,比如:
> (setf z 3) 3 > z 3使用def而不使用setf来定义变量是有优势的,那就是def会记录它定义过的变量的名称,并允许使用variables函数找出可用的变量。setf还有一些其他用法,那些我们等到3.8节再讲。
练习 2.11
略。
2.4.6 读取数据文件
两个可用的读取数据的文件是read-data-columns和read-data-file。
第一个是read-data-columns,是被设计来读取包含一些数据列的文件的。它带两个参数:表示文件名的字符串和一个整数,表示文件里的列数。它返回一个列表集的列表,其中每一列都放到一个列表里。数据里的每项可以由任意数目的空格分开,但是不能用逗号和其它标点符号。每项可能是任何合法的Lisp表达式,特别地,他们可以是数字、字符串或符号。所有的列必须是等长的。返回的结果列表里的内容都可以使用select函数提取。
假设我们有一个叫做mydata的文件,包含两列数字数据。我们想要读取这些数据并将数据列分别命名为x和y,我们可以首先读取整个文件并将结果保存到名为mydata的变量里:
> (def mydata (read-data-columns "mydata" 2))现在,变量mydata的值是一个包含两个数字列表的列表。为了提取和命名这两个数据列表,我们可以用如下表达式:
> (def x (select mydata 0)) > (def y (select mydata 1))
read-data-columns的第二个参数是可选的。如果没提供,那么数据的列数将由从第一个非空行开始的所有数目确定。
在有的系统上,文件名参数也可能是可选的,如果忽略了该参数,将出现一个对话框以选择要读取的文件。
如果数据文件不是按列形式组织的,你可以使用read-data-file函数读取文件的所有内容,并以单独一个列表的形式返回。该列表可以使用Lisp-Stat函数操作成为合适的形式。文件条目是为read-data-columns准备的,函数read-data-file带单一参数,是一个要读取的文件名的字符串,有的系统里你可以忽略这个参数,并使用对话框选择要读取的文件。
这两个函数能够满足大多数的需求,如果你必须要读取非指定格式的文件,你可以使用lisp的原始的文件处理函数,这些将在第4.5节描述。
2.5 动态绘图
在第2.2节里,我们使用直方图和散点图来测试单变量和两个变量之间关系的分布情况。本节我们将介绍一些动态绘图方法和可以探头3个或多个变量之间关系的绘图技术。前4个小节的绘图技术和方法很简单,仅需要一些鼠标操作和简单的命令。第5小节将介绍绘图对象的概念,还有从解释器向一个对象发送消息的方法。这些想法是用来向散点图里加入直线和曲线。对象和消息的基本概念在2.6节回归模型一节里还要用到。最后一小节将展示如何使用Lisp迭代器来构造动态模拟动画,一副运动的图形。
2.5.1 旋转图
在探索多个变量之间的关系的时候,我们很自然会想到构造一个数据的三维散点图。当然,我们只能在显示屏上看到一个该图形的二维投影,任何关于该数据的你能通过线性模型感知到的图形深度信息都会丢失。一个试图恢复图形深度感知的方法就是绕着某一坐标轴旋转这些点。spin-plot函数允许你构造一个能够旋转的三维图形。
举个例子,让我们看一些收集好的数据,来检测一下材料损耗量(当橡胶样本与研磨材料一起摩擦式发生的)与标本两个属性之间的关系,硬度和抗拉强度。 硬度用邵氏度来度量,抗拉强度用kg/cm²度量,研磨损失用g/马力小时度量。数据可以这样输入:
> (def hardness
(list 45 55 61 66 71 71 81 86 53 60 64 68 79 81 56 68 75
83 88 59 71 80 82 89 51 59 65 74 81 86))
HARDNESS
> (def tensile-strength
(list 162 233 232 231 231 237 224 219 203 189 210 210 196
180 200 173 188 161 119 161 151 165 151 128 161 146
148 144 134 127))
TENSILE-STRENGTH
> (def abrasion-loss
(list 372 206 175 154 136 112 55 45 221 166 164 113 82
32 228 196 128 97 64 249 219 186 155 114 341 340
283 267 215 148))
ABRASION-LOSS 表达式
> (spin-plot (list hardness tensile-strength abrasion-loss)) #<Object: 136b4f8, prototype = SPIN-PROTO>将产生一幅图形。
图2.7 磨损数据的旋转图
spin-plot函数的参数是一个含有3个list或vector类型的list,表示x, y, z三个变量。初始条件下z轴垂直屏幕并指向屏幕外部。你可以将鼠标放到Pitch、Roll和Yaw前的小方框里,然后点击鼠标来旋转图形。通过旋转图形,你可以看到所有点几乎落到同一个平面上。
图2.8 磨损数据的第二个视图
图2.8展示的数据基本在一个平面上。因此,线性模型应该能提供合理的修正。事实上,在执行一段时间的旋转操作之后,你会注意到数据点会有轻微的扭曲,暗示了存在一些二阶项成分。不幸的是,在打印图里这部分信息很难传达给用户。
spin-plot函数的一些选项可以被指定为关键字参数,给:title关键字传递一个字符串就可以为绘图窗体制定一个可替换的标题,关键字:variable-labels可以用来提供一个可以替换的坐标轴标签,如使用一个字符串列表替换x、y和z。例如,对于磨损数据你可以使用一下表达式来构建图形来代替上边我们给出的表达式:
> (spin-plot (list hardness tensile-strength abrasion-loss)
:title "Abrasion Loss Data"
:variable-labels (list "Hardness"
"Tensile Strength"
"Abrasion Loss"))
#<Object: 142b29c, prototype = SPIN-PROTO> 函数spin-plot还可以接收关键字参数:scale,如果:scale赋值为t(t也是其默认值),那么数据将三个变量的均值进行中心化,这三个变量都将被尺度化以适应图形尺寸;如果:scale赋值为nil,数据将被假定尺度化为-1到1之间,图形将绕原点旋转。如果你想要以变量的均值来中心化你的图形,并且用相同的量尺度化所有的观测值的话,可以使用该表达式:
> (spin-plot
(list (/ (- hardness (mean hardness)) 140)
(/ (- tensile-strength (mean tensile-strength)) 140)
(/ (- abrasion-loss (mean abrasion-loss)) 140))
:title "Abrasion Loss Data"
:variable-labels (list "Hardness"
"Tensile Strength"
"Abrasion Loss")
:scale nil)
#<Object: 145f7c0, prototype = SPIN-PROTO> 每一个Lisp-Stat绘图窗口都提供了一个菜单栏,用来与图形进行通信。使菜单
精确的可用的方式依赖于窗体管理系统。在Macintosh操作系统的XLISP-STAT里,当图形窗口是前置窗口时,图形的菜单是放在菜单栏里的;在XLISP-STAT的X11版本里,窗体上有一个按钮来弹出菜单。可旋转的图形上的菜单允许你改变速度与角度,或者是否使用深度感知,是否显示坐标轴等。默认情况下,图形是使用深度感知的:离观察者近的点总比离观察者远的点绘制的大些。
大多数窗口系统都有提供一个修改鼠标点击的惯例,目的是区别本次点击是想要开始一次文本选择做点击,还是想要扩展已存在的选择而做的点击。Macintosh操作系统的处理方式是点击鼠标的时候按下shift键,来发出一个扩展信号。换句话说,shift键就是Macintosh的扩展修改器。在旋转的图形里,不使用扩展修改器的话,在Pitch、Roll或者Yaw方框里点击鼠标将引起图形的旋转。在合适的扩展修改器上一直按着鼠标不放将引起图形不停地旋转甚至是释放鼠标释放之后,旋转将在你再次点击旋转控制面板的时候才会停止(注:经本人测试,该操作在Windows操作系统的XLISP-STAT同样适用)。
练习2.12
略。
练习2.13
略。
2.5.2 散点图矩阵
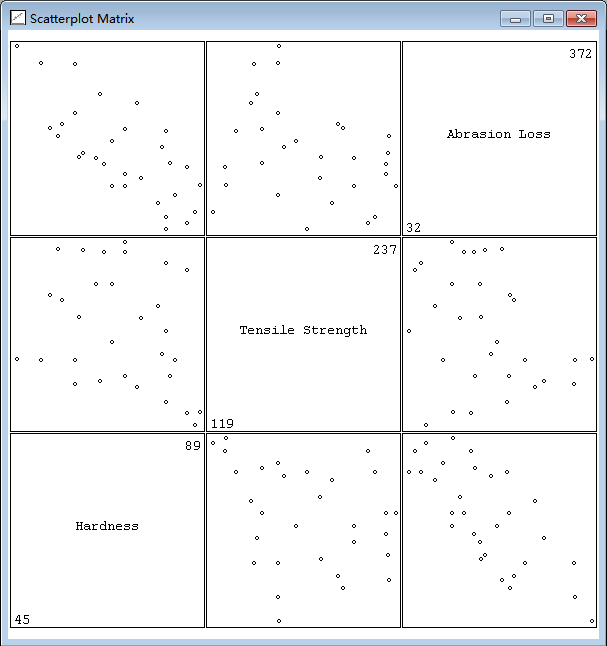
另一个绘制变量集的方法是查看变量间所有可能散点图组合矩阵。scatterplot-matrix函数将提供这样一幅图形。使用上节提到的磨损数据,
> (scatterplot-matrix (list hardness tensile-strength abrasion-loss) :variable-labels (list "Hardness" "Tensile Strength" "Abrasion Loss")) #<Object: 142b78c, prototype = SCATMAT-PROTO>
表达式产生散点图矩阵,如图2.9。
图2.9 磨损数据的散点图矩阵
"磨损"相对"抗拉强度"那幅图形给了我们关于这两个变量的联合变量的想法,但是此时"硬度"这个变量也随着点的不同而不同。为了获得这3个变量之间关系的理解,我们最好将“硬度”这个变量固定在一个可变的水平,然后观察当我们改变硬度这个变量时,"磨损"和"抗拉强度"这两个变量之间的关系是怎样变化的。通过使用两个高亮技术:selecting和brushing,你可以在散点图矩阵里进行诸如此类的探索。
选择模式. 当鼠标时一个箭头的时候,表示你的图形处于选择模式,这是默认的设置。在这个模式里你可以移动箭头鼠标到一个点上然后点击鼠标来选择一个点。为了选择一组点,可以在目标点上拖出一个选择框。如果某些点不能包含到选择框了,你可以通过“拖选扩展”操作加入那些点,即按住shift键再拖选或点选(Macintosh和Windows操作系统同样适用)。如果你不用扩展修改器(即shift键),任何已选的元素都会变为非选择状态;当你适用扩展修改器时,应经选择的点仍然是选择状态。
刷模式.你可以通过绘图菜单的Mouse Mode项,在弹出的对话框里选择Brushing来进入刷模式。在这个模式里,光标看起来像一把刷墙的刷子和一个附在它上边的虚线框。当你在图形里移动刷子的时候,在刷子内部的点是高亮的。刷子外的点没有高亮,除非是已经被选中的。为了在刷模式下选择点(让它们永久高亮),你需要在移动鼠标时保持鼠标按下。
在图2.10的统计图例,“硬度”变量的中间部分的点已经被用一把长且窄的刷子高亮了。通过使用绘图菜单的Resize Brush命令,可以改变刷子的大小。在磨损对抗拉强度那幅图里,你可以看到高亮的点看起来是沿着一条曲线分布的。如果你想拟合一个模型到这些数据上,本次观测结果建议根据曲率来拟合模型。这与观测这些数据旋转得到的结论是相似的。
通过选择而高亮数据在旋转的图形中是有用的。通过选定一个变量的一小片具有相似值得数据点,然后旋转它,你可以检测给定的一个固定变量情况下,其它的两个变量的条件分布的三维结构。
散点图矩阵在检测一个定量变量和几个分类变量之间的关系时是很有用的。在第2.4.1节里我们看到了一些关于马铃薯种植的实验数据,这些数据用到了3个马铃薯品种和4种种植密度。图2.11展示了这些数据的散点图。该图使用一个长且窄的刷子来高亮第三个品种的数据点。如果品种和密度之间没有相互作用,那么当刷子从一个品种移动另一个品种上的时候,高亮点的形状应该大至是以平行的方式移动的。
与spin-plot函数相似,scatterplot-matrix函数也接受可选的关键字参数:title, :variable-labels和:scale。
练习2.14
略。
练习2.15
略。
2.5.3 与单个图形交互
旋转的图形和散点图矩阵都是交互性的统计绘图。简单的散点图也允许一些交互。如果你选择菜单里的Show Labels选项,挨着高亮点将出现一个标签。你可以使用选择模式或刷模式来高亮一个点,默认的标签可能是"0", "1", ...这样的形式,大多数绘图函数都允许你使用:point-labels关键字参数来提供一个可替换的标签列表。
在查看大量数据集的时候有一个选项是很有用的,那就是移除一部分点,你可以这么做,选择要移除的点,然后选择菜单里的Remove Selection菜单项。使用菜单里的Remove Selection可以完成窗口尺寸的重新调整。
当选中绘图窗口里的点集时,你可以使用Selection Symbol菜单项来改变显示点的符号。如果你的系统支持使用颜色,你可以使用Selection Color菜单项来设置选中点的颜色。
通过绘图窗口菜单的Selection... 菜单项,你可以保存一个变量里当前选中点的指标。然后将弹出对话框让你输入一个名字。当没有选择点时,你可以使用Selection...菜单项来指定随后选择的点的指标(注:该功能可以将任意点集编成一组,并通过Selection...菜单项,使用名称来选中、高亮。)。将弹出一个对话框让你输入一个表达式,用来确定所选点的指标(注:即所选点的符号),这个表达式可以是任意Lisp表达式,可以是单独指标或者指标列表。(注:个人认为这里的指标译为符号更容易理解,实际上就是起个名字)
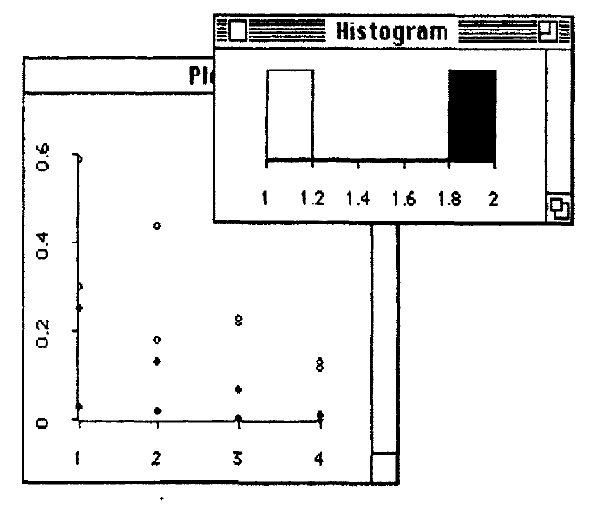
图2.12连接了以下两种数据,乙醇相对氧气水平的散点图和针对发酵数据的糖类型指标直方图。来自于同一组的糖是高亮的。
2.5.4 连接图
当你在散点图矩阵里刷取或选择的时候,你可以看下这组散弹图的其它图形的相互作用。通过选择你想要连接的那个图形的菜单的Link View选项,你可以构建自己的交互图集。例如,2.5.2节练习2.14的数据,我们可以把乙醇和氧气放到散点图里,把糖放到直方图里。如果我们连接这两个图形,然后选择直方图里两个糖数据中的一个,散点图里对应的点就会高亮,就像图2.12中显示的那样。
图 2.12 乙醇相对氧气水平的散点图和针对发酵数据的糖类型指标直方图
如果你想用特定标签来选择数据点,你可以使用name-list函数来生成带标签的窗体。这个窗体可以被连接到任何图形里,选择在命名列表里的一个标签,与之连接的那个图形上的相对应的点就会高亮。你可以使用带一个数值参数的name-list函数,例如,(name-list 10)产生带有标签"0", ..., "9"的命名列表,你也可以给出一个你自己的命名列表标签。练习 2.16
略。
2.5.5 修改散点图
在产生一个数据集的散点图之后,你可能想要加一条线到图形上,例如一条回归线。作为例证,一项自行车道对车手的影响的研究,自行车手到马路中间线的距离,自行车手与正通过的汽车的距离,记录10个自行车手。数据输入如下:
> (def travel-space
'(12.8 12.9 12.9 13.6 14.5 14.6 15.1 17.5 19.5 20.8))
TRAVEL-SPACE
> (def separation
'(5.5 6.2 6.3 7.0 7.8 8.3 7.1 10.0 10.8 11.0))
SEPARATION 伴随随机变量separation,可以拟合这些数据的回归线有如下特征:截距为-2.18,斜率为0.66。让我们看一下如何将这条线加到数据的散点图的。
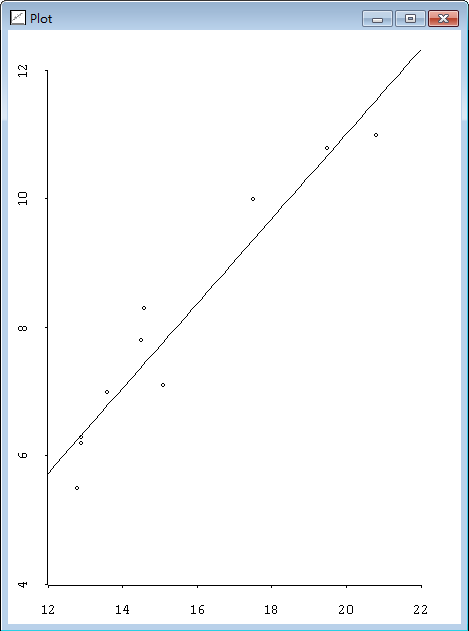
我们可以使用如下表达式来产生这些数据点的散点图:
> (plot-points travel-space separation) #<Object: 1376d30, prototype = SCATTERPLOT-PROTO>为了能向图形中加线,我们必须能够在Lisp-Stat中引用到它。为了完成这个任务,我们可以将plot-points函数返回的结果赋值给一个符号,即:
> (def myplot (plot-points travel-space separation)) MYPLOTplot-points函数返回的结果就是一个Lisp-Stat对象。为了使用该对象,你需要向它发送一个消息,这要使用send函数来完成,其一般形式为: (send <object> <message selector> <argument1> ... )
如下表达式将通知myplot添加一条a+bx的线,其中a=-2.18, b=0.66,。<message selector>是:abline这一关键字,数字-2.18和0.66是参数。消息由选择器和参数组成。消息选择器一般是一个Lisp关键字,也就是说它们是一个带冒号的符号。结果见图2.13。
图2.13 带拟合直线的自行车数据散点图
散点图对象还能理解一些其它消息,包括:help消息:
> (send myplot :help) loading in help file information - this will take a minute ...done SCATTERPLOT-PROTO Scatterplot Help is available on the following: ABLINE ACTIVATE ADD-FUNCTION ADD-LINES ADD-METHOD ADD-MOUSE-MODE ADD-POINTS ADD-SLOT ADJUST-POINTS-IN-RECT ADJUST-SCREEN ADJUST-SCREEN-POINT ADJUST-TO-DATA ALL-POINTS-SHOWING-P ALL-POINTS-UNMASKED-P ALLOCATE ANY-POINTS-SELECTED-P APPLY-TRANSFORMATION BACK-COLOR BRUSH BUFFER-TO-SCREEN CANVAS-HEIGHT CANVAS-TO-REAL CANVAS-TO-SCALED CANVAS-WIDTH CENTER CHOOSE-MOUSE-MODE CLEAR CLEAR-LINES CLEAR-MASKS CLEAR-POINTS CLICK-RANGE CLIP-RECT CLOSE CONTENT-ORIGIN CONTENT-RECT CONTENT-VARIABLES COPY-TO-CLIP CURRENT-VARIABLES CURSOR CUT-TO-CLIP DELETE-DOCUMENTATION DELETE-METHOD DELETE-MOUSE-MODE DELETE-SLOT DISPOSE DO-CLICK DO-IDLE DO-KEY DO-MOTION DOC-TOPICS DOCUMENTATION DRAG-GREY-RECT DRAW-BITMAP DRAW-BRUSH DRAW-COLOR DRAW-DATA-LINES DRAW-DATA-POINTS DRAW-LINE DRAW-MODE DRAW-POINT DRAW-STRING DRAW-STRING-UP DRAW-SYMBOL DRAW-TEXT DRAW-TEXT-UP ERASE-ARC ERASE-BRUSH ERASE-OVAL ERASE-POLY ERASE-RECT ERASE-SELECTION ERASE-WINDOW FIND FIXED-ASPECT FOCUS-ON-SELECTION FRAME-ARC FRAME-LOCATION FRAME-OVAL FRAME-POLY FRAME-RECT FRAME-SIZE GET-METHOD H-SCROLL-INCS HAS-H-SCROLL HAS-METHOD HAS-SLOT HAS-V-SCROLL HELP HIDE-WINDOW IDLE-ON INTERNAL-DOC ISNEW LINE-TYPE LINE-WIDTH LINESTART-CANVAS-COORDINATE LINESTART-COLOR LINESTART-COORDINATE LINESTART-MASKED LINESTART-NEXT LINESTART-TRANSFORMED-COORDINATE LINESTART-TYPE LINESTART-WIDTH LINKED LOCATION MARGIN MASK-SELECTION MENU METHOD-SELECTORS MOUSE-MODE MOUSE-MODE-TITLE MOUSE-MODES MOVE-BRUSH NEW NUM-LINES NUM-POINTS NUM-VARIABLES OWN-METHODS OWN-SLOTS PAINT-ARC PAINT-OVAL PAINT-POLY PAINT-RECT PARENTS PASTE-FROM-CLIP PASTE-STREAM PASTE-STRING POINT-CANVAS-COORDINATE POINT-COLOR POINT-COORDINATE POINT-HILITED POINT-LABEL POINT-MASKED POINT-SELECTED POINT-SHOWING POINT-STATE POINT-SYMBOL POINT-TRANSFORMED-COORDINATE POINTS-HILITED POINTS-IN-RECT POINTS-SELECTED POINTS-SHOWING PRECEDENCE-LIST PRINT PROTO RANGE REAL-TO-CANVAS REDRAW REDRAW-CONTENT REMOVE REPARENT REPLACE-SYMBOL RESIZE RESIZE-BRUSH RETYPE REVERSE-COLORS ROTATE-2 SCALE SCALE-TO-RANGE SCALE-TYPE SCALED-RANGE SCALED-TO-CANVAS SCREEN-RANGE SCROLL SELECTION SELECTION-DIALOG SELECTION-STREAM SET-MODE-CURSOR SET-OPTIONS SET-SELECTION-COLOR SET-SELECTION-SYMBOL SHIFT SHOW SHOW-ALL-POINTS SHOW-WINDOW SHOWING-LABELS SIZE SLICE-VARIABLE SLOT-NAMES SLOT-VALUE START-BUFFERING TEXT-ASCENT TEXT-DESCENT TEXT-WIDTH TITLE TRANSFORMATION UNDO UNMASK-ALL-POINTS UNSELECT-ALL-POINTS UNSHOW-ALL-POINTS UPDATE USE-COLOR V-SCROLL-INCS VARIABLE-LABEL VIEW-RECT VISIBLE-RANGE WHILE-BUTTON-DOWN X-AXIS Y-AXIS NIL对所有的散点图来说,它们的主题列表都是相似的,但是对旋转图、散点图矩阵和直方图来说有一些不同。
:clear消息,就像它的名字暗示的那样,它会清除绘制的图形并允许从头开始创建一个新的图形。另外两个有用的消息是:add-points和:add-lines。为了查明如何使用它们,我们可以使用:help消息并将:add-points和:add-lines作为参数:
> (send myplot :help :add-points) ADD-POINTS Method args: (points &key point-labels (draw t)) or: (x y &key point-labels (draw t)) Adds points to plot. POINTS is a list of sequences, POINT-LABELS a list of strings. If DRAW is true the new points are added to the screen. For a 2D plot POINTS can be replaced by two sequences X and Y. NIL
> (send myplot :help :add-lines) ADD-LINES Method args: (lines &key type (draw t)) or: (x y &key point-labels (draw t)) Adds lines to plot. LINES is a list of sequences, the coordinates of the line starts. TYPE is normal or dashed. If DRAW is true the new lines are added to the screen. For a 2D plot LINES can be replaced by two sequences X and Y. NIL描述里的术语sequence意思是一个list或者一个vector。
图2.13里的统计图展示了数据的曲率。在travel-sapce里,separation一次项和二次项的回归计算将产生一些估计系数——常数估值为-16.42,一次项系数估值为2.433,二次项系数估值为-0.05339。让我们使用:clear, :add-points和:add-lines消息改变myplot对象,用来显示我们拟合后的二次模型。首先我们使用表达式定义x来表示从点12到点22之间的50等份的变量,定义y作为这些值的拟合响应。
> (def x (rseq 12 22 50)) X > (def y (+ -16.42 (* 2.433 x (* -0.05339 (* x x))))) Y
图2.14 带拟合曲线的自行车数据散点图
然后用下边的表达式将图形改成图2.14的样子。> (send myplot :clear) NIL > (send myplot :add-points travel-space separation) NIL > (send myplot :add-lines x y) NIL我们已经使用plot-points来获得一个新的图形,然后又用:add-lines修改了图形,但是这里我们用到的方法允许我们尝试所有这3个消息。
2.5.6 动态模拟
作为“通过修改现有统计图形我们能干什么”的有一个例证,让我们来构建一个动态模拟来检测变量,这些变量来自于标准正态分布样本的直方图,这个动态模拟就是一个小电影。为了开始,使用如下表达式构建一个单变量的直方图然后保存它的绘图对象为h。
> (def h (histogram (normal-rand 20))) H:clear消息对直方图也是可用的,就像我们在它的帮助信息里看到的那样:
> (send h :help :clear) CLEAR Message args: (&key (draw t)) Clears the plot data. If DRAW is nil the plot is redrawn; otherwise its current screen image remains unchanged.它带一个可选的关键字函数。如果这个参数是nil,那么统计图不会重画直到一些其它消息导致它重画,这对动态模拟式很重要的。倒换和重新调整窗体大小,直到当你输入命令到解释器时仍能看到直方图窗口为止。(注:其实不用那么麻烦,在菜单栏的windows->Tile直接将所有窗口平铺就行了)然后输入表达式:
> (dotimes (i 50)
(send h :clear :draw nil)
(send h :add-points (normal-rand 20))) 这应该能产生一个50个直方图的序列,每一个都基于一个大小为20的正态分布样本。通过输入关键字参数:draw并赋值nil给:clear消息,你就能保证每个直方图都在屏幕上待一会儿直到下一个直方图准备绘制的时候。再次运行这个例子,不带这个参数,看看有什么不同。
编程实现动态模拟提供了另一个查看一些变量之间关系的方法。作为一个简单的例子,假设我们想检测标量abrasion-loss和hardness之间的关系,这些变量来自第2.5.2节。我们用下边的表达式生成一个abrasion-loss变量的直方图:
> (def h (histogram abrasion-loss)) H对于动态模拟来说,:point-selected, :point-hilited和:point-showing消息是很有用的。以下是直方图里对:point-selected消息的信息:
> (send h :help :point-selected) POINT-SELECTED Method args: (point &optional selected) Sets or returns selection status (true or NIL) of POINT. Sends :ADJUST-SCREEN message if states are set. Vectorized.
如此你可以使用这个消息检测一个点当前是不是选中状态,也可以选中或者取消选中。再次倒换窗口到输入命令时能够看到直方图,然后键入表达式:
> (dolist (i (order hardness))
(send h :point-selected i t)
(send h :point-selected i nil)) 表达式(order hardness)将产生一个hardness的有序值列表,从而返回结果的第一个元素是hardness的第一个元素,第二个元素是hardness的第二小的元素,以此类推。对相应数据的循环移动进行选择与取消选择操作。
屏幕上的结果与从左到右刷hardness变量直方图的结果是相似的,hardness直方图是与abrasion-loss变量的直方图相连接的。这种方法的缺陷就是与用鼠标实现相比,写出表达式很难。换句话说,当你用鼠标刷图形数据的时候,你趋向于将经历集中在你刷的图形上而不是另一个连接图上。当你运行一个动态模拟图时,当模拟程序运行的时候你什么也不用做,因此可以将所有精力集中在结果上。
一个中间方案是可行的:你可以设置一个带滚动条的对话框,滚动条的值就是(order hardness)列表的所有值,当它滚动的时候就会选择相应的点,2.7节将展示这种方案如何工作的例子。
在很多Lisp系统里,就像我们现在描述的这个模拟器一样,偶尔会停一会儿,原因就是需要垃圾回收机制来动态地回收已经分配的存储单元。虽说是这样,在一些简单的模拟器里,比如这些迭代器对你来说,可能仍然太快了而不能捕捉任何处理的形式。为了降低速度,你可以用函数pause来加入一个短的延时,通过使用一个整数n,pause将导致可执行程序的挂起,大约要n/60秒钟,例如,你可以使用下式代替前边的表达式:
> (dolist (i (order hardness))
(send h :point-selected i t)
(pause 10)
(send h :point-selected i nil)) 这将确保循环将以大概每秒6个的速度穿过数据点。
练习 2.17
略。
练习 2.18
略。
2.6 回归
回归模型是使用Lisp-Stat的对象和消息传递机制实现的。这在2.5.5节已经介绍了。再继续阅读之前,你可能需要简单复习一下那节内容。
让我们来对2.5.5节的自行车数据做一个简单的拟合。因变量是separation,自变量是tranvel-space。为了形成回归模型,可以使用regression-mode函数:
> (regression-model travel-space separation) Least Squares Estimates: Constant -2.18247 (1.05669) Variable 0 0.660342 (6.747931E-2) R Squared: 0.922901 Sigma hat: 0.582108 Number of cases: 10 Degrees of freedom: 8 #<Object: 141cbbc, prototype = REGRESSION-MODEL-PROTO>regression-model函数的基本语法是(regression-model <x> <y>)。对于一个简单的回归模型,<x>可以是一个列表的列表、矢量的列表或者一个矩阵。regression-model函数也包含一些可选参数,包括:intercept, :print和:weights,:intercept和:print的默认参数都是t,想要获得一个没有截距的模型,使用以下表达式:
> (regression-model x y :intercept nil)为了形成一个带权重的回归模型,使用以下表达式:
> (regression-model x y :weights w)这里的w是一个与y长度相等的权重列表或权重矢量,假设误差方差与权重w成反比。
regression-model函数打印拟合模型的简单概述,并且返回一个模型对象。为了能够进一步检测模型,用以下表达式将返回的模型对象赋给一个变量:
> (def bikes (regression-model travel-space separation :print nil)) BIKES
值为nil的关键字参数:print压缩了我们看到的模型的概述。为了找出那些消息时可用的,我们使用:help消息:
> (send bikes :help) loading in help file information - this will take a minute ...done REGRESSION-MODEL-PROTO Normal Linear Regression Model Help is available on the following: ADD-METHOD ADD-SLOT BASIS CASE-LABELS COEF-ESTIMATES COEF-STANDARD-ERRORS COMPUTE COOKS-DISTANCES DELETE-DOCUMENTATION DELETE-METHOD DELETE-SLOT DF DISPLAY DOC-TOPICS DOCUMENTATION EXTERNALLY-STUDENTIZED-RESIDUALS FIT-VALUES GET-METHOD HAS-METHOD HAS-SLOT HELP INCLUDED INTERCEPT INTERNAL-DOC ISNEW LEVERAGES METHOD-SELECTORS NEW NUM-CASES NUM-COEFS NUM-INCLUDED OWN-METHODS OWN-SLOTS PARENTS PLOT-BAYES-RESIDUALS PLOT-RESIDUALS PRECEDENCE-LIST PREDICTOR-NAMES PRINT PROTO R-SQUARED RAW-RESIDUALS REPARENT RESIDUAL-SUM-OF-SQUARES RESIDUALS RESPONSE-NAME RETYPE SAVE SHOW SIGMA-HAT SLOT-NAMES SLOT-VALUE STUDENTIZED-RESIDUALS SUM-OF-SQUARES SWEEP-MATRIX TOTAL-SUM-OF-SQUARES WEIGHTS X X-MATRIX XTXINV Y NIL
这些消息里很多都是自解释的,很多已经被:display消息使用了,regression-model函数将:display消息发送给新的模型并打印其概述信息。作为一个例子,让我们试一下:coef-estimates和:coef-standard-errors消息:
> (send bikes :coef-estimates) (-2.182471511502903 0.6603418619651689) > (send bikes :coef-standard-errors) (1.0566881307586837 0.06747931359188968) >按理说,如果模型里有截距的话,由这些消息返回的列表里的实体是与截距对应的,当提供给regression-model函数的时候,该截距后边跟着因变量。然而,如果在计算过程中探测到了退化现象,在拟合过程中一些变量就不会被使用,在打印的概述信息里它们将被用别名的方式标记出来。已经使用的变量的标度将由:basis消息获取,如果合适的话,由:coef-estimates返回的列表项将与截距对应,与截距一起的还有各元素的系数。消息:x-matrix和:xtxinv是相似的。
:plor-residuals消息产生一个残留的统计图,为了查明残留的统计图针对什么,让我们看一下它的帮助信息吧:
> (send bikes :help :plot-residuals) loading in help file information - this will take a minute ...done PLOT-RESIDUALS Message args: (&optional x-values) Opens a window with a plot of the residuals. If X-VALUES are not supplied the fitted values are used. The plot can be linked to other plots with the link-views function. Returns a plot object. NIL使用以下两个表达式,我们可以构架图2.15所示的两个数据统计图:
> (plot-points travel-space separation) #<Object: 1350994, prototype = SCATTERPLOT-PROTO> > (send bikes :plot-residuals travel-space) #<Object: 1357680, prototype = SCATTERPLOT-PROTO>
图2.15 针对自行车实例连接原始数据和残存图的示意图
通过连接这些统计图(注:使用菜单栏里的plot->link view菜单选项),我们可以使用鼠标在两个统计图里同步识别数据点。图中一个标号为6的点脱颖而出。
这两幅统计图表明数据是存在曲率的,如果我们忽略观测点6,残留图的曲率特别明显。为了允许这个曲率的出现,我们可以试图用二阶项对travel-space变量来拟合出一个模型。
> (def bikes2
(regression-model (list travel-space (^ travel-space 2))
separation))
Least Squares Estimates:
Constant -16.4192 (7.84827)
Variable 0 2.43267 (0.971963)
Variable 1 -5.339121E-2 (2.922567E-2)
R Squared: 0.947792
Sigma hat: 0.512086
Number of cases: 10
Degrees of freedom: 7
BIKES2 我使用幂指数函数“^”来计算travel-space变量的平方,即我们形成了一个多元回归模型,该回归模型的第一个参数是一个自变量的列表。
从这个点开始你可以向多个方向继续前进,如果你想计算观测点的库克距离(注:统计学专有名词,详见连接),你可以向bikes2对象发送:cooks-distance消息:
> (send bikes2 :cooks-distances) (0.16667299257295504 0.009185959754912747 0.030268009774083452 0.011098970664932503 0.009584417522457393 0.12066535826085792 0.5819289720128115 0.04601789946507566 0.006404473564781199 0.09400811436381019)为了检测这个距离,你可以首先计算内部学生化残差,
> (def studres (/ (send bikes2 :residuals)
(* (send bikes2 :sigma-hat)
(sqrt (- 1 (send bikes2 :leverages))))))
STUDRES
然后再获取距离的方式,
> (* (^ studres 2)
(/ (send bikes2 :leverages)
(- 1 (send bikes2 :leverages))
3))
(0.16667299257295504 0.009185959754912747 0.030268009774083452 0.011098970664932505 0.009584417522457393 0.12066535826085789 0.5819289720128115 0.046017899465075666 0.006404473564781199 0.09400811436381019)
来直接计算它们。第7个数据元素——下标从0开始的观测点6,很明显地脱颖而出。
检测残留图中可能的异常值的另一个方法是就是使用贝叶斯残留图,该方法是由Chaloner和Brant倡导的,可以使用:plot-bayes-residuals消息获得该功能。以下表达式将产生图2.16所示的统计图。
> (send bikes2 :plot-bayes-residuals) #<Object: 131b5a0, prototype = SCATTERPLOT-PROTO>
图2.16 自行车数据的贝叶斯残留图
图2.16中条形显示的意思是实际实现误差的后验分布的±2SD,它基于对回归系数的一个不当的均匀先验分布。(注:这句话可能不太准确,请参照原文),y轴是以σ为单位的。从而本图展示了一个盖然率,数据点6偏离平均值为3或更大标准方差的盖然率大约是3%;偏离平均值至少2个单位标准协方差的盖然率在50%上下。
练习 2.19
略。
练习 2.20
略。
2.7 定义函数和方法
本节将对Lisp-Stat的一个简洁的介绍。最基础的编程操作是定义函数。与其紧密相关的是为对象定义一个方法。
2.7.1 定义函数
用来定义函数的特殊形式叫defun,最简单的defun语法形式是 (defun <name> <parameters> <body>),这里的<name>是一个符号,用来作为函数名,<parameters>是符号的一个列表,命名为参数,<body>表示一个或多个表达式,组成了函数体。例如,假设你想要定义一个函数从一个列表里删除一个元素,函数应该将列表和你想删除的元素的下标作为参数。函数体可以基于上边2.4.3节描述的两个方法中的一种。这里是其中的一个:
> (defun delete-case (x i)
(select x (remove i (iseq (length x)))))
DELETE-CASE
defun的参数都没有被引用(即没有在符号前加单引号):defun是一个特殊形式,不需要对参数求值。
你可以写一个向对象传递消息的函数。这里有一个函数,它带两个回归模型变量参数,假设这些模型是被嵌套的,为了比较这些模型来计算F-统计:
> (defun f-statistic (m1 m2)
"Args: (m1 m2)
Computes the F statistic for testing model m1 within model m2."
(let ((ss1 (send m1 :sum-of-squares))
(df1 (send m1 :df))
(ss2 (send m2 :sum-of-squares))
(df2 (send m2 :df)))
(/ (/ (- ss1 ss2) (- df1 df2)) (/ ss2 df2))))
F-STATISTIC 这个函数定义使用Lisp的let构造来建立一些局部变量。变量ss1, df1, ss2, df2是为模型参数m1和m2定义的,之后用来计算F统计。参数列表后的字符串叫文档字符串。当defun表达式出现文档字符串的时候,defun将它安装在函数内部供help函数获取。
2.7.2 函数作为参数
在第2.2.3节中,我们使用plot-funcion来绘制[-pi, pi]范围内的正弦函数。你可以使用相同的方法来绘制你自己的函数。例如,假设你想绘制-2到3范围内的f(x)=2x+x^2的图形,你可以定义一个函数f:
> (defun f (x) (+ (* 2 x) (^ x 2))) F然后使用plot-function:
> (plot-function #'f -2 3)回忆一下,表达式#'f是(function f)的缩写,用来获得与符号f关联的那个Lisp函数。
使用spin-function你可以构建一个有两个变量的函数的旋转图形,例如,定义f为:
(defun f (x y) (+ (^ x 2) (^ y 2))) F那么以下表达式将构建一个自变量x在[-1, 1]内,自变量y在[-1, 1]内的函数f(x, y)=x^2+y^2的函数图像,该图像用6X6网格表示,网格点的数量可以使用:num-points关键字改变。结果如图2.17所示。
contour-function函数的必选参数数量与spin-function函数相同,将产生一个函数参数的轮廓线图。除了:num-points关键字,你也可以赋予contour-function函数:levels关键字,紧跟着一个轮廓等级的列表。
本例中,不得不定义一个函数仅仅是作为另一个函数的参数,这种方法有些笨拙。能够写一个产生我们所需功能的表达式,然后将这个表达式作为plot-function和spin-function的参数,这样可能更方便一些。第3.6.1节将展示如何完成这个任务。
练习 2.21
2.73 绘图动画控制
作为函数使用的另一种展示,假设在Box-Cox能量变换中(Box-Cox变换是统计建模中常用的一种数据变换,用于连续的响应变量不满足正态分布的情况),我们想检测改变指数对正态概率图形造成的影响。
第一步,定义函数以计算幂转换,并正规化转换结果,使它落在0和1之间:
> (defun bc (x p)
(let* ((bcx (if (< (abs p) .0001) (log x) (/ (^ x p) p)))
(min (min bcx))
(max (max bcx)))
(/ (- bcx min) (- max min))))
BC 这个定义里使用了let*形式来建立一个局部变量的绑定。let*形式与上边用到的let形式相似,但在一下几点是不同的,let*顺序地定义变量,允许使用在let*中定义的其它变量来定义一个新的变量,相反地,let并行地创建其分配符。在这种情况下,变量min和max根据bcx来定义。
然后,我们需要一个正数集合来做变换,让我们来使用2.2.1节里介绍的降水量数据样本,我们需要对观测值进行排序:
> (def x (sort-data precipitation)) X期望的统一顺序统计的常态分布分位数由下式给出:
> (def nq (normal-quant (/ (iseq 1 30) 31))) NQ未经转换的数据的概率统计图由下式构建:
> (def myplot (plot-points nq (bc x 1))) MYPLOT因为这里的幂是1,所以函数bc仅仅是对数据进行了尺寸调整。
为了改变myplot对象的转换中幂的值,我们可以定义一个change-power函数:
> (defun change-power (p)
(send myplot :clear :draw nil)
(send myplot :add-points nq (bc x p)))
CHANGE-POWER 想这样对一个新表达式求值:
> (change-power .5)然后对新的幂值,实例中的平方根转换,重画统计图,
我们可以使用不同的幂值重复这个处理过程,目的是获取转换的影响的感觉,不是这个方法是很笨拙的。一个可代替的方法就是设置一个滑动对话框来控制这个幂的值。这个滑动的对话框是一个无模式的对话框,包含一个滑块和一个显示的值域。当滑块移动的时候,显示值改变,同时动作触发。这里的动作由动作函数定义,这个函数使用当前滑块的值作为参数进行调用,每次这个值由用户改变,我们可以用如下表达式构建针对我们的问题的一个合适滑块:
> (sequence-slider-dialog (rseq -1 2 31) :action #'change-power)
这个滑块可以通过以下值进行移动, -1.0, -0.8, ..., 1.8, 2.0,每次调用的时候都使用当前的移动滑块得到的幂值。图形和滑块见图2.18所示。
图2.18 一个滑块控制幂转换的统计图
2.7.4 定义方法
当消息发送给对象的时候,对象系统对象和消息选择器来查找最合适的代码段执行。从而,不同的对象对相同的消息作出不同的响应,线性回归模型和非线性回归模型都会对:coef-estimates消息进行响应,但是他们会执行不同的代码来计算该响应。
对象使用的用来响应消息的代码叫做方法。对象被组织在层级关系里,在那里对象从它们祖先那里继承其它对象。如果一个对象没有它自己的用来响应消息的方法,它就会使用从祖先那里继承的方法。send函数将提升该对象的祖先的列表的优先级,直到找到针对消息的方法。
大多数我们目前接触到的对象都是直接继承自原型对象。Scatterplots(散点图)继承自scatterplot-proto,histograms(直方图)继承自histogram-proto,回归模型对象继承自regression-model-proto。原型对象与其它任何对象都是相似的,它们是定义一定类别的对象的典型版本,这类对象定义了默认的行为。但是任何对象都有一个方法,在调试新方法的过程中,最好将这个方法连接到独立构建的对象上,达到代替原型的目的。
defmeth宏用来向对象添加方法。方法定义的一般形式是:(def <object> <selector> <parameters> <body>),<object>是一个将拥有新方法的对象,参数<selector>是对方法的消息选择关键字,参数<parameters>是方法的参数名列表,<body>是组成方法体的一个或多个表达式。当方法被使用时,这些表达式将按顺序求值。
作为一个简单的展示,在第2.5.6节我们使用一个循环运行一个模拟器,在那里我们在一幅直方图里展示了大小为20的样本序列,该序列来源于一个正态分布。原始的直方图由下式构建:
> (def h (histogram (normal-rand 20))) H每次迭代的时候,我们首先清除直方图,然后增加一个新的样本,通过为新消息定义一个方法,我们可以简化一下我们的直方图:
> (defmeth h :new-sample ()
(send self :clear :draw nil)
(send self :add-points (normal-rand 20)))
:NEW-SAMPLE 运行50次动画的循环现在可以写成这样:
> (dotimes (i 50) (send h :new-sample))在为:new-sample消息的方法定义时需要一点解释,self变量的实用。对象的方法经常需要能够参考获取消息的对象,因为方法可以被继承,在写方法的时候,你可能对接受的对象的标识不是很确定。因此对象系统使用了一个惯例,当表达式在被求值的消息对应的那个方法的里时,接收对象就是变量self的值。
现在我们有一个简单的消息,用来向我们的直方图发送消息,告诉他显示一条新数据样本。拥有一个发送消息的简单的办法,而不需要向解释器敲入命令,这样好极了。直方图菜单提供了一个方便的工具来达到该目的,表达式是:
> (let ((m (send h :menu))
(i (send menu-item-proto :new "New Sample"
:action #'(lambda () (send h :new-sample)))))
(send m :append-item i)) 向直方图的菜单末端加入一个新的菜单项,每次选中该菜单项的时候都将改变显示的数据样本。在阅读过第6和第7章之后,你将能够理解这个表达式。
2.8 更多模型和技术
Lisp-Stat为非线性回归模型、最大似然估计和近似贝叶斯推理提供了一些工具。这三个工具集的共同特点是描述一个特定问题所需要的部分信息是函数提供的,例如,一个为非线性回归设立的函数。本节假设你熟悉非线性回归基础,最大似然估计和贝叶斯推理:
2.8.1 非线性回归
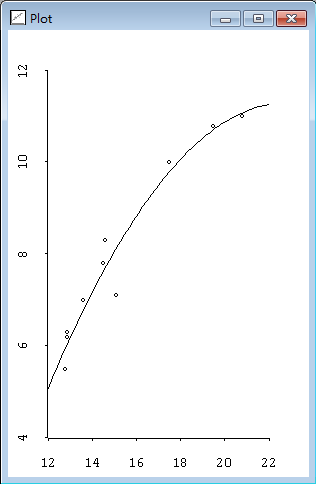
Lisp-Stat允许非线性的正态回归模型。举个例子,Bates和Watts描述了一个变量y和变量x之间关系的试验,变量y表示酶促反应的速度,变量x表示底物浓度。试验中的浓度和观测速度由下式给定,试验中使用嘌呤霉素对酶促反应进行处理:
> (def x1 (list .02 .02 .06 .06 .11 .11 .22 .22 .56 .56 1.1 1.1)) X1 > (def y1 (list 76 47 97 107 123 139 159 152 191 201 207 200)) Y1 >对于速度对底物浓度的依赖,米氏函数通常可以提供一个好的模型。
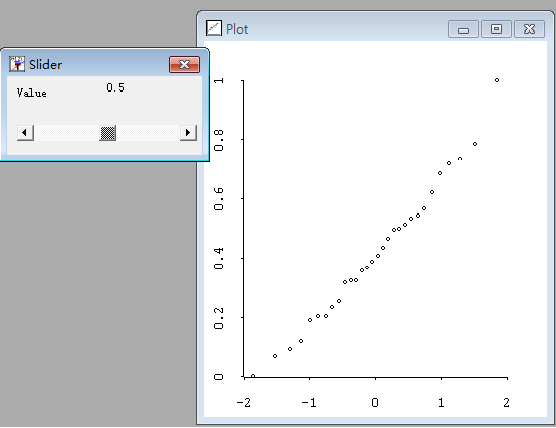
假定在一个给定的浓度水平上,米氏函数代表平均速度,其函数f1定义为:
> (defun f1 (theta)
(/ (* (select theta 0) x1) (+ (select theta 1) x1)))
F1 f1函数将对参数列表theta的平均反应时间的列表进行计算,这是在
数据点x1处做的计算。
使用这些定义,我们可以使用nreg-model函数构建一个非线性回归模型。首先,我们需要对两个模型的参数进行初始化估计,为米氏模型检测表达式这一操作显示,当x增长时,米氏函数逼近一条渐近线,θ0。第二个参数θ1可以解释成当函数达到渐近线一半时x的值。利用这些对参数的解释,下式将构造一个统计图,图示见图2.19,我们可以对θ0读出200,对θ1读出0.1这些合理的初始化估计。
图2.19 酶促反应试验的底物浓度对反应速度的统计图
nreg-model函数需要的参数有平均值函数、响应矢量和参数的初始估计列表。nreg-model函数通过使用一个交互式的算法来计算精确的估计值,这个交互式的算法以初始猜测凯斯,打印结构的概要,并返回一个非线性回归模型对象:
> (def puromycin (nreg-model #'f1 y1 (list 200 .1))) Residual sum of squares: 7964.19 Residual sum of squares: 1593.16 Residual sum of squares: 1201.03 Residual sum of squares: 1195.51 Residual sum of squares: 1195.45 Residual sum of squares: 1195.45 Residual sum of squares: 1195.45 Residual sum of squares: 1195.45 Least Squares Estimates: Parameter 0 212.684 (6.94715) Parameter 1 6.412127E-2 (8.280941E-3) R Squared: 0.961261 Sigma hat: 10.9337 Number of cases: 12 Degrees of freedom: 10 PUROMYCIN
nreg-model函数也带一些关键字参数,包括用:epsilon来制定一个收敛准则,用:count-limit做为迭代次数的极限值,这两个值得默认值分别为0.0001和20。使用值为nil的:verbose关键字来抑制每次迭代过程的的平方和残差信息,使用值为nil的:print关键字将约束概述信息,拟合模型的算法是一个带回溯简单高斯-牛顿算法,导数是通过数值计算的。
为了使你明了如何进一步分析模型,你可以向puromycin对象发送:help消息。结果与线性回归模型的帮助信息相似。原因很简单:非线性回归模型是用对象实现的,而非线性回归模型的原型nreg-model-proro是继承自线性回归模型的原型的。内部数据、计算估计值的方法和计算拟合值得方法都做了修改以适应非线性模型,但是其它大多数方法都没有改变。一旦模型完成拟合,预估参数值得平均函数的雅克比矩阵将被定义为X矩阵来使用。在此定义的术语中,大多数针对线性回归的方法,像:coef-standard-errors和:leverages等,仍然是有意义的,至少是一阶逼近的。
除了可以相应线性回归模型的消息之外,非线性回归模型还能相应以下消息:
- :COUNT-LIMIT
- :EPSILON
- :MEAN-FUNCTION
- :NEW-INITIAL-GUESS
- :PARAMETER-NAMES
- :THETA-HAT
- :VERBOSE
练习 2.23
略。
练习 2.24
略。
2.8.2 最大和最小似然估计
Lisp-Stat有两个函数可以求得一些变量的最大似然率。第一个是newtonmax函数,它带一个函数和一个列表或者矢量值来表示初始猜测值,该初始猜测针对最大值的位置,函数试图用基于带回溯的牛顿法来找到最大值。该算法基于Dennis和Schnabel描述的无约束的最小系统。
举个例子,Proschan描述了定时收集的一些数据,这些数据源自几个飞机场空调单元拓机的时间间隔。其中一个机场的数据输入如下:
> (def x (list 90 10 60 186 61 49 14 24 56 20 79 84 44 59 29 118
25 156 310 76 26 44 23 62 130 208 70 101 208))
X 这些数据的一个简单的模型作出如下假设:拓机时间间隔是独立随机变量,满足通用gamma分布,gamma分布的密度可以写成这样:
这里的μ是拓机时间的平均值,β是gamma的形状参数,那么该数据样本的log似然函数应该这样给出:
我们可以定义一个Lisp函数来计算这个log似然函数:
> (defun gllik (theta)
(let* ((mu (select theta 0))
(beta (select theta 1))
(n (length x))
(bym (* x (/ beta mu))))
(+ (* n (- (log beta) (log mu) (log-gamma beta)))
(sum (* (- beta 1) (log bym)))
(sum (- bym)))))
GLLIK 该定义使用函数log-gamma对log(Γ(β))。
封闭形式的最大似然概率估计最这个分布的形状参数是不可用的,但是我们可以使用newtonmax函数来用数值方法进行计算。我们需要一个厨师猜测值用来作为最大似然的起始值。为了获得初始估计,我们可以计算x的期望和标准方差:
> (mean x) 83.51724137931036 > (standard-deviation x) 70.80588186304823然后使用矩估计方法估计
> (^ (/ (mean x) (standard-deviation x)) 2) 1.3912770125276501使用这些起始值,我们可以最大化log似然函数:
> (newtonmax #'gllik (list 83.5 1.4)) maximizing... Iteration 0. Criterion value = -155.603 Iteration 1. Criterion value = -155.354 Iteration 2. Criterion value = -155.347 Iteration 3. Criterion value = -155.347 Reason for termination: gradient size is less than gradient tolerance. (83.51726798264603 1.670986791540375)一些状态信息打印出来用于继续优化。通过使用值为nil的:verbose关键字,你可以关闭这些信息。
你可能想要检查这个函数的确接近0的梯度。如果对这个梯度没有一个封闭的表达式的话,你可以用numgrad函数计算一个用数值上的近似值。对于我们的例子:
> (numgrad #'gllik (list 83.5173 1.67099)) (-4.072480396396883E-7 -1.2576718377326971E-5)梯度的元素确实相当接近0.
你也可以计算二阶导数,或者使用numhess函数计算Hessian矩阵。最大似然估计的近似标准差可以这样给定,先对最大值处的Hessian矩阵取负,再求逆矩阵,再去该逆矩阵的对角线元素,最后对其求平方根:
> (sqrt
(diagonal
(inverse (- (numhess #'gllik (list 83.5173 1.67099))))))
(11.997551713830456 0.40264778727213846) 使用newtonmax代替求取最大值,然后分别计算二阶导数。通过使用值为t的关键字参数:return-derivs,你可以让newtonmax返回一个元素位置列表,该列表的元素包括最大值、最有函数值、梯度和Hessian矩阵。
牛顿法假设函数是两次可微的,如果你的函数不平滑,或者如果你因为其它原因对使用newtonmax存在麻烦。你可能要尝试第二个最大化函数,nelmeadmax函数,该函数接收一个函数和一个初始化猜测值,然后试图用Nelder-Mead单纯形法找打最大值,该方法是由Press、Flannery、Teukolsky和Vetterling描述的。初始猜测值由一个单点组成,它以n个数字的列表或矢量的形式展现。初始猜测值也可能是一个单形,即一个n维问题的n+1个点的列表。如果你制定了一个单点,那你也应该使用:size关键字参数去指定一个列表或者矢量,其长度为n,且需要在初始单形的每一个维度里指定。这应该展示初始范围的大小,在那个范围里算法将开始它的搜索直到找到最大值,我们可以在我们都额gamma例子里使用这个方法:
> (nelmeadmax #'gllik (list 83.5 1.4) :size (list 5 0.2)) Value = -155.52959743506827 Value = -155.52959743506827 Value = -155.52959743506827 Value = -155.5294988579447 Value = -155.46938588692785 Value = -155.46938588692785 Value = -155.42198557523471 Value = -155.42198557523471 Value = -155.40996834939776 Value = -155.3866822915446 Value = -155.38103392707978 Value = -155.36281930571423 Value = -155.36281930571423 Value = -155.34979141245745 Value = -155.34979141245745 Value = -155.34935123123307 Value = -155.3470397238531 Value = -155.3470397238531 Value = -155.3469673747863 Value = -155.34689776692113 Value = -155.3468231506837 Value = -155.3468231506837 Value = -155.34680431458563 Value = -155.34680431458563 Value = -155.3467951205185 Value = -155.34679314554154 Value = -155.3467903355422 Value = -155.3467903355422 Value = -155.346789572537 Value = -155.3467892236572 Value = -155.3467892236572 Value = -155.3467892236572 Value = -155.3467892236572 (83.5156874768436 1.6711172274500135)这个方法与牛顿法相比有些长,但是它确实获得了相同的结果。
练习 2.25
略。
2.8.3 近似贝叶斯计算
本小节描述的函数可以用来计算后验矩的一阶和二阶近似值,还有一阶边际后验密度的鞍点状近似。基于文献[62,63,64],近似值假定后验密度是光滑的,并且以单模式为主。
让我们从一个简单的例子开始,一份关于白血病患者存活时间和病人体内白细胞数量的关系的研究数据集,该数据以周为单位。该数据由两类病人组成,AG+和AG-型。17个AG+型病人的数据可以输入如下:
> (def wbc-pos (list 2300 750 4300 2600 6000 40500 10000 17000
5400 7000 9400 32000 35000 100000 100000
52000 100000))
WBC-POS
> (def times-pos (list 65 156 100 134 16 108 121 4 39 143 56
26 22 1 1 5 65))
TIMES-POS 高白细胞数量表示处在疾病的比较严重的阶段,也就是存活的机会更低。
针对这些数据会用到一个模型:假设存活时间是按指数分布的,它带一个平均值参数,该平均值参数使用log-linear方法将"白细胞数量的对数"这一非线性指标进行"对数变换"以得到线性模型,然后它才可用于线性回归模型之中。为了方便,我将对白细胞数量数据扩大10,000倍。也就是说,一个病人白细胞数量WBCi对应的平均存活时间为
这里的xi=log(WBCi/10000)。log似然函数给定为:
这里的yi代表存活时间。计算转换后的WBC变量为:
> (def transformed-wbc-pos (- (log wbc-pos) (log 10000))) TRANSFORMED-WBC-POS之后可以用以下函数计算log似然率:
> (defun llik-pos (theta)
(let* ((x transformed-wbc-pos)
(y times-pos)
(theta0 (select theta 0))
(theta1 (select theta 1))
(t1x (* theta1 x)))
(- (sum t1x)
(* (length x) (log theta0))
(/ (sum (* y (exp t1x)))
theta0))))
LLIK-POS 我将使用一个模糊的、不确定的先验分布来看待这个问题,该分布在θi>0范围内十个常量;从而,log后验密度与上边构造的log似然函数式等价的,最多多出一个常数。第一步就是用bayes-model函数构造一个贝叶斯模型对象。该函数可以接受一个计算log后验分布密度的函数和这个后验模型的初始猜测数据,该函数通过这个初始猜测数据的交互方法计算后验模型,并打印后验分布信息的简短概述,然后返回一个模型对象。我们可以使用函数llik-pos来计算log后验密度,所以所有我们能做的就是对后验模型的初始值估计。因为我们使用的模型假设是一个线性关系,是表示平均存活时间的对数与转换后的WBC变量的线性关系。,对transformed-wbc-pos变量的存活时间的对数的一个线性回归模型应该提供一个合理的估计,该线性回归模型这样给出:
> (regression-model transformed-wbc-pos (log times-pos)) Least Squares Estimates: Constant 3.58281 (0.328336) Variable 0 -0.736302 (0.225778) R Squared: 0.414869 Sigma hat: 1.32459 Number of cases: 17 Degrees of freedom: 15 #<Object: 13daa98, prototype = REGRESSION-MODEL-PROTO>所以说模型的合理初始猜测评估值是θ0评估值=exp(3.5),θ1的评估值=0.8,现在我们可以将这些评估值放到bayes-model函数里:
> (def lk (bayes-model #'llik-pos (list (exp 3.5) 0.8))) maximizing... Iteration 0. Criterion value = -96.3803 Iteration 1. Criterion value = -87.4612 Iteration 2. Criterion value = -85.2634 Iteration 3. Criterion value = -84.8285 Iteration 4. Criterion value = -84.7883 Iteration 5. Criterion value = -84.7877 Iteration 6. Criterion value = -84.7877 Reason for termination: gradient size is less than gradient tolerance. First Order Approximations to Posterior Moments: Parameter 0 60.6309 (15.0481) Parameter 1 0.390576 (0.175448) LK通过使用值为nil的:print关键字参数,来压缩概述信息是可能的。可以使用:verbose关键字压缩迭代信息。
bayes-model函数打印的概述信息给出了参数的后验均值和标准方差的一阶近似值。也就是说均值是由后验模型的元素近似得到的,标准方差是由模型的log后验值得负Hessian矩阵的逆矩阵的对角线元素的平方根得到的。这些近似值也可以通过向模型发送:lstmoments消息来获得:
> (send lk :1stmoments) ((60.63089554959938 0.3905764020242036) (15.048125818750082 0.1754475290888174))结果是两个列表值的列表结构,它们是平均值列表和标准方差列表。
一个相对较慢但是一般情况下更精确的二阶近似值也是可用的。它可以使用:moments获得:
> (send lk :moments) ((69.89109467010141 0.4033868081199018) (18.577055399066786 0.1829812572509589)) > (send lk :moments (list 0 1)) ((69.89109467010141 0.4033868081199018) (18.577055399066786 0.1829812572509589))θ0的一阶近似值和二阶近似值有一点不同,特别是,看起来平均值比模型的大些。这表明参数的后验分布是向右倾斜的,通过查看近似边际后验密度图我们可以确认这一点。消息:marginl带一个指标参数,还有一个进行密度求值的点数据序列,最后以列表形式返回它的值,该列表的元素就是使用的序列和在这些数据点处的近似密度值。为了产生一个边际密度图,该列表可以使用plot-lines函数给出:
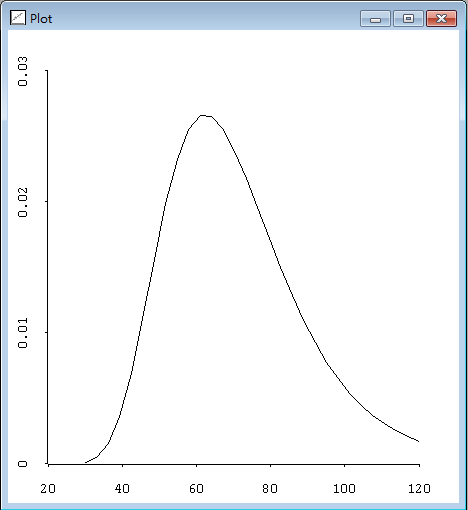
> (plot-lines (send lk :margin1 0 (rseq 30 120 30))) #<Object: 1401734, prototype = SCATTERPLOT-PROTO>结果见图2.20所示,确实看到图形有些向右倾斜。
图2.20 θ0的近似边际后验分布
除了检测单独参数,也可以查看参数的光滑函数的后验分布。例如,你可能想问一个WBC=50000的病人存活一年以上的概率,那么该方法包含了什么信息,概率如下:
其中
x=log(5),可以由以下函数计算:
> (defun lk-sprob (theta)
(let* ((time 52.0)
(x (log 5))
(mu (* (select theta 0)
(exp (- (* (select theta 1) x))))))
(exp (- (/ time mu)))))
LK-SPROB 该函数可以使用:1stmoments, :moments和:margin1方法来近似计算函数的后验矩和边际后验密度。对于这些矩的结果是又有不同并且带有正向的倾斜:
> (send lk :1stmoments #'lk-sprob) ((0.20026961686731173) (0.10757618146651714)) > (send lk :moments #'lk-sprob) ((0.24368499587543843) (0.11571130867154422))边际密度可以这样表示:
> (plot-lines (send lk :margin1 #'lk-sprob (rseq .01 .8 30))) #<Object: 13d338c, prototype = SCATTERPLOT-PROTO>结果如下图:
图2.21 WBC=50000的病人一年存活概率的近似边际后验密度
基于本图,数据显示其存活率几乎肯定低于0.5,但是很难做出一个更精确的说法了。
在本小节描述的函数式基于前一小节的优化的代码。默认情况下,导数是用数值方法计算的。如果你想自行计算导数,你可以让你的log后验函数返回这样一个列表,它包含函数值和梯度,或者包含函数值、梯度和Hessian矩阵。在较大的问题里,在做二阶近似的时候可能需要精确的导数值。
练习2.26
略。
练习2.27
略。