再译《A *路径搜索入门》之二

■路径评分

Path Scoring

计算出的路径时，确定要使用的方格的关键是下面的公式：

The key to determining which squares to use when figuring out the path is the following equation:

 

F = G + H

 

■这里

where

 

G =从起点A沿着生成的路径移动到一个给定的方形网格上运行成本。

G = the movement cost to move from the starting point A to a given square on the grid, following the path generated to get there.

 

H =从格子中给定方块移动到最终目的地，B点的估计的运行成本。这通常称为启发式，这可有点混乱。因为是一个猜测所以这样称呼。在找到路径之前，我们真的不知道实际的距离，因为各种各样的事情都在途中（墙，水等）。在本教程中给出一个计算H的方法，但在网络上你能找到许多计算H方法的其他文章。

H = the estimated movement cost to move from that given square on the grid to the final destination, point B. This is often referred to as the heuristic, which can be a bit confusing. The reason why it is called that is because it is a guess. We really don't know the actual distance until we find the path, because all sorts of things can be in the way (walls, water, etc.). You are given one way to calculate H in this tutorial, but there are many others that you can find in other articles on the web.

 

通过反复遍历开启列表，选择具有最小F值的方块来生成我们的路径。在本文中这个过程将有进一步更详细的描述。首先来仔细看看如何计算公式。

Our path is generated by repeatedly going through our open list and choosing the square with the lowest F score. This process will be described in more detail a bit further in the article. First let's look more closely at how we calculate the equation.

 

如上所述，G是从起始点移动到给定点所生成路径的运动成本。在这个例子中，我们将指定每个移动水平或垂直方成本为10，对角线移动成本为14。我们使用这些数字是因为斜角移动是2的平方根（不要害怕），是水平或垂直移动的大约1.414倍。我们使用10和14是为了简单起见。比例大致是正确的，又能避免计算平方根和小数。这不只是因为我们是愚笨的，不喜欢数学。采用这些数字是让计算机更快，太快了。你很快就会发现，如果你不使用这些捷径，路径搜索可能会很缓慢的。

As described above, G is the movement cost to move from the starting point to the given square using the path generated to get there. In this example, we will assign a cost of 10 to each horizontal or vertical square moved, and a cost of 14 for a diagonal move. We use these numbers because the actual distance to move diagonally is the square root of 2 (don't be scared), or roughly 1.414 times the cost of moving horizontally or vertically. We use 10 and 14 for simplicity's sake. The ratio is about right, and we avoid having to calculate square roots and we avoid decimals. This isn't just because we are dumb and don't like math. Using whole numbers like these is a lot faster for the computer, too. As you will soon find out, pathfinding can be very slow if you don't use short cuts like these.

 

由于我们计算G值是沿特定的路径给定的平方，该办法找出那个方块的父亲的G值，然后加10或14取决于它从父方格是正交（非对角线）还是对角线。需要这种方法将在本实施例进一步上变得明显一点，因为我们得到一个以上的方块。

Since we are calculating the G cost along a specific path to a given square, the way to figure out the G cost of that square is to take the G cost of its parent, and then add 10 or 14 depending on whether it is diagonal or orthogonal (non-diagonal) from that parent square. The need for this method will become apparent a little further on in this example, as we get more than one square away from the starting square.

 

H可以用各种方式估计。我们在这里使用的方法被称为曼哈顿方法，在这里计算从当前方块到目标方水平和垂直方向移动方块的总数，忽略对角运动，忽略可能在过程中的任何障碍。然后，我们将总数乘以10，我们的成本水平或垂直移动一格。这是（可能）被称为曼哈顿方法，因为它像计算城市街区的数量从一个地方到另一个地方，在那里你不能穿过块对角。

H can be estimated in a variety of ways. The method we use here is called the Manhattan method, where you calculate the total number of squares moved horizontally and vertically to reach the target square from the current square, ignoring diagonal movement, and ignoring any obstacles that may be in the way. We then multiply the total by 10, our cost for moving one square horizontally or vertically. This is (probably) called the Manhattan method because it is like calculating the number of city blocks from one place to another, where you can't cut across the block diagonally.

 

阅读本说明，您可能已经猜到了启发式仅仅是当前方格与目标之间的剩余距离的一个“像乌鸦飞似的”粗略的估计。不是这种情况。我们实际上试图估计沿路径的剩余距离（通常是更远）。越接近我们的估计是实际剩余距离，就会越快的算法。如果我们高估了这个距离，但是，它不能保证给我们的最短路径。在这样的情况下，我们有所谓的“不可接受启发式”。

Reading this description, you might guess that the heuristic is merely a rough estimate of the remaining distance between the current square and the target "as the crow flies." This isn't the case. We are actually trying to estimate the remaining distance along the path (which is usually farther). The closer our estimate is to the actual remaining distance, the faster the algorithm will be. If we overestimate this distance, however, it is not guaranteed to give us the shortest path. In such cases, we have what is called an "inadmissible heuristic."

 

从技术上讲，在这个例子中，曼哈顿方法是不可接受的，因为它稍稍高估了剩下的距离。但是我们会用也无妨，因为它是一个更容易理解我们的目的，因为它只是一个轻微的高估。在极少的情况下，得到的路径不是最短的，这将是近短。想了解更多？你你可以在这里（http://www.policyalmanac.org/games/heuristics.htm）找到方程和附加说明启发式。

Technically, in this example, the Manhattan method is inadmissible because it slightly overestimates the remaining distance. But we will use it anyway because it is a lot easier to understand for our purposes, and because it is only a slight overestimation. On the rare occasion when the resulting path is not the shortest possible, it will be nearly as short. Want to know more? You can find equations and additional notes on heuristics here.

 

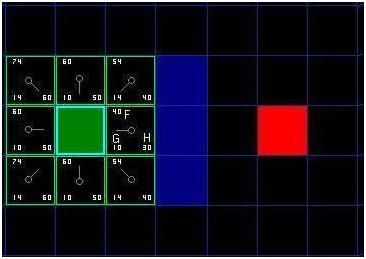
F是G加H中的和。搜索的第一个步骤的结果可以从下面的说明中看出。在F，G和H的分数被写入在每个方格。正如在紧挨着开始方块右侧的方块上，F被打印在左上角，G印在左下方，而H显示在右下方。

F is calculated by adding G and H. The results of the first step in our search can be seen in the illustration below. The F, G, and H scores are written in each square. As is indicated in the square to the immediate right of the starting square, F is printed in the top left, G is printed in the bottom left, and H is printed in the bottom right.

 

[图3]

[Figure 3]

 

所以，让我们来看看其中的一些方块。在有字母的方块上，G = 10，这是因为它是在一个水平方向的距离起始方块仅一个方格。正方形紧邻上方，下方，及在起始方格的左边有10相同的G值，对角线方块有14个G值。

So let's look at some of these squares. In the square with the letters in it, G = 10. This is because it is just one square from the starting square in a horizontal direction. The squares immediately above, below, and to the left of the starting square all have the same G score of 10. The diagonal squares have G scores of 14.

 

H值是通过估计到红色目标方块的曼哈顿距离，仅移动水平和垂直方向，而忽略墙上那就是在计算方式。使用这种方法，方块上开始的直接右边3格是红格，为30。那么高于这个方块的方块的H值是4格距离（记住，只能水平移动和垂直）的一个H值40.你也许可以看到了为其他方块计算H值的方法。

The H scores are calculated by estimating the Manhattan distance to the red target square, moving only horizontally and vertically and ignoring the wall that is in the way. Using this method, the square to the immediate right of the start is 3 squares from the red square, for a H score of 30. The square just above this square is 4 squares away (remember, only move horizontally and vertically) for an H score of 40. You can probably see how the H scores are calculated for the other squares.

 

每个方格的F值，再次，只是通过加G和H一起计算。

The F score for each square, again, is simply calculated by adding G and H together.

（待续）