第三章學題 Ansi Common Lisp, Paul Graham
1. Show the following lists in box notation:
(a)
(a b (c d))
(b)
(a (b (c (d))))
(c)
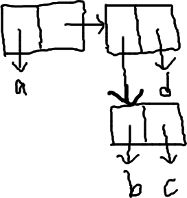
(((a b) c) d)
(d)
(a (b . c) . d)
2. Write a version of union that preserves the order of the elements in the original lists:
> (new-union '(a b c) '(b a d)) (A B C D)
3. Define a function that takes a list and returns a list indicating the number of times each (eql) element appears, sorted from most common element to least common:
> (occurences '(a b a d a c d c a)) ((A . 4) (C . 2) (D . 2) (B . 1))
4. Why does
(member '(a) '((a) (b)))
return nil?
5. Supose the function pos+ takes a list and returns a list of each element plus its position:
> (pos+ '(7 5 1 4)) (7 6 3 7)
Define this function using (a) recursion, (b) iteration, (c) mapcar.
6. After years of deliberation, a government commission has decided that lists should be represented by using cdr to point to the first element and the car to point to the rest of the list. Define the government versions of the following functions:
(a) cons
(b) list
(c) length (for lists)
(d) member (for lists; no keywords)
7. Modify the program in Figure 3.6 to use fewer cons cells. (Hint: Use dotted lists.)
(defun compress (x)
(if (consp x)
(compr (car x) 1 (cdr x))
x))
(defun compr (elt n lst)
(if (null lst)
(list (n-elts elt n))
(let ((next (car lst)))
(if (eql next elt)
(compr elt (+ n 1) (cdr lst))
(cons (n-elts elt n)
(compr next 1 (cdr lst)))))))
(defun n-elts (elt n)
(if (> n 1)
(list n elt)
elt))
8. Define a function that takes a list and prints it in dot notation:
> (showdots '(a b c)) (A . (B . (C . NIL))) NIL
9. Write a program to find the longest finite path through a network represented as in Section 3.15.
(defun shortest-path (start end net)
(bfs end (list (list start)) net))
(defun bfs (end queue net)
(if (null queue)
nil
(let ((path (car queue)))
(let ((node (car path)))
(if (eql node end)
(reverse path)
(bfs end
(append (cdr queue)
(new-paths path node net))
net))))))
(defun new-paths (path node net)
(mapcar #'(lambda (n)
(cons n path))
(cdr (assoc node net))))
The network may contain cycles.
解
1.
(a)
(b)
(c)
(d)
2.
recursive
(defun uunion (og sec)
(if (null sec)
og
(if (member (car sec) og)
(uunion og (cdr sec))
(uunion (append og (list (car sec))) (cdr sec)))))
iterative
(defun uunion (og sec)
(let ((rs (list (car og))))
(dolist (obj (append og sec))
(pushnew obj rs))
(reverse rs)))
3
(defun occur (ll)
(let ((nu nil))
(dolist (obj ll)
(if (assoc obj nu)
(setf (cdr (assoc obj nu))(+ 1 (cdr (assoc obj nu))))
(push (cons obj 1) nu)))
(sort nu #'> :key #'cdr)))
4
member 用 eql, 會比較記憶體位置和没有記憶體的數字與没有記憶體的 abcd 字, eq 比純記憶體, equal 比印的一不一樣
(member '(a) '((a) (b)) :test #'equal)
5
iteration
(defun addadd (ll)
(let ((nu nil)(temp 0))
(dolist (obj ll)
(setf nu (cons (+ temp obj) nu))
(setf temp (+ temp 1)))
(reverse nu)))
recursive
(defun addadd (ll)
(adda ll 0))
(defun adda (ll what)
(if (null ll)
nil
(cons (+ (car ll) what) (adda (cdr ll) (+ 1 what)))))
mapcar
(defun addadd (ll)
(let ((tmp -1))
(mapcar #'(lambda (x)
(setf tmp (+ tmp 1))
(+ x tmp))
ll)))
6
(a) cons
(defun mycons (x y)
(let ((tmp '(nil . nil)))
(setf (car tmp) x
(cdr tmp) y)
tmp))
(b) list