用递归解决冒泡排序问题
冒泡排序是种很简单的排序方式。如果用循环方式,通常就是两层循环。
由于两层循环都是与元素个数N线性相关,所以可以简单估算出它的时间复杂度是O(N2),通常而言,这是较糟糕的复杂度。
当然,这也几乎是所有简单方式的宿命,想简单就别想效率高!
前面篇章说到递归也是一种循环,所以普通循环能解决的问题,用递归也能解决。我们来看看怎么写出它来。
定义好接口先
首先啰嗦几句写代码习惯问题:
要有服务意识,要有API意识。
先把接口定义好,与具体的实现分开。另外则作一些基本的判断,内部实现就不需要再作判断了,也能简化内部实现:
// 对外接口
public static void sort(int[] array) {
if (array != null && array.length > 1) {
bubbleSort(array);
}
}
// 具体内部实现
private static void bubbleSort(int[] array) {
// TODO
}
想更加通用就用Comparable接口,不过这些不是这里的重点,这里就简单用array了。
主体结构
前面说到,递归分成基本情形(base case)和递归情形(recursive case),所以,不管三七二十一,先把主体结构写出来:
private static void bubbleSort(int[] array) {
// TODO
if (baseCase) {
return;
} else {
// 1. do something maybe
// ...
// 2. 递归调用
// bubbleSort(xxx);
}
}
base case
这个简单,当只有一个元素时,自然就无需排序了,所以:
if (array.length == 1) {
return;
}
显然,base case没做任何事,因此只要把代码条件反转一下,就可以省略掉这个base case了。
recursive case
如何找出递归模式呢?我们从一个具体的事例考虑:
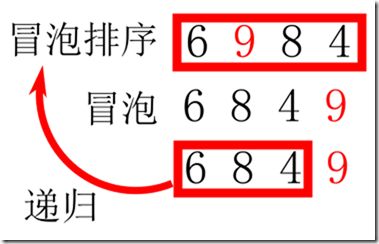
假如有四个元素:6 9 8 4,假设向右边冒泡,那么从左向右两两比较并根据情况决定是否交换:
第一次比较6和9,6比9小,无需交换,继续;
第二次比较9和8,9比8大,所以交换它们得到: 6 8 9 4;
第三次比较9和4,9比4大,交换,得到6 8 4 9。
那么,经过一轮冒泡之后,最大的元素9已经冒泡到了最右边上,然后下一步就可以只考虑剩下的三个元素了,而这正好可视作一个新的待排序的数组。
先不考察冒泡的细节,用一个抽象的bubble表示它,那么可以归纳出如下递归模式:
bubbleSort一个元素为N的数组就是:
进行一轮冒泡(bubble),
然后对左边的N-1个元素(子数组)递归地进行bubbleSort。
如下图示:
据此,写出以下代码(省略了base case):
private static void bubbleSort(int[] array) {
// TODO pseudo code
if (array.length > 1) {
bubble(array);
bubbleSort(array.subArray(0, array.length - 1));
}
}
你可能会想,array并没有subArray方法呀,另外应该是在原数组上排序。没错,这里也注明了这是伪代码(pseudo code),此刻只需要思考抽象的逻辑是否有问题即可,诸如是否会发生无限递归呀等情况。
敲定细节
代码中还是伪代码的形式,显然我们是要在原数组上排序,这使得我们必须增加一个显式的参数
如果array有更加对象化的方法来能直观表示subArray(并非指复制的那种,而是一种指向新位置的引用),那么增加参数就不是必要的了。目前我们无法摆脱array的结构限制去思考。(这其实暴露了java在表达能力上的缺陷或者说array的设计上存在一些问题,使得我们只能笨拙地去表达我们想要的意思)
根据前面的归纳,定为N-1来表示子数组subArray:
bubbleSort(n – 1, array);
注:你可能忍不住会把这里的n想像成array的index。没错,它最终是要映射到index上,但此刻你只要抽象地从概念上把握它即可,这里的n就是指n个元素,它不是什么index。
方法要形成递归,所以定义处也修改,增加一参数n:
private static void bubbleSort(int n, int[] array)
公共接口里调用时也因此要作改动,需要显式传入N,对于初始情况,N也即是array.length:
bubbleSort(array.length, array);
另外有一点要特别注意,因为不是传递subArray,array.length始终不变,所以if语句中的判断已经不正确:
必须由if(array.length > 1)改为if(n > 1)
现在考察bubble,显然N跟array都要往里面传。现在直接将bubble方法考虑成递归的,以减少中间环节。那么,还要再增加一个参数bn,表示有几个元素需要bubble。
让IDE生成方法签名,最终结果如下:
// 对外接口
public static void sort(int[] array) {
if (array != null && array.length > 1) {
bubbleSort(array.length, array);
}
}
// 具体内部实现
private static void bubbleSort(int n, int[] array) {
if (n > 1) {
bubble(n, n, array);
bubbleSort(n - 1, array);
}
}
private static void bubble(int bn, int n, int[] array) {
// TODO
}
注:bubble(n, n, array)中第一个n表示有n个元素需要冒泡,第二个n表示有n个元素需要排序。
其实你也能感觉到,这完全就是面向过程式的编程。
至此,主体结构已经OK了。现在考虑冒泡bubble的实现问题。
冒泡子过程
冒泡同样可视作一个递归的过程。按着一样的思路,先是一个大体的框架:
private static void bubble(int bn, int n, int[] array) {
if (baseCase) {
return;
} else {
// 1. do something
// ...
// 2. 递归调用
// bubble(xx, n, array);
}
}
base case
显然,bn=1时表示只有一个元素,就无需冒泡了,直接返回:
if (bn == 1) {
return;
}
显然,这一case也是可以省略的。
recursive case
其实就是一个从左到右不断比较与交换的过程。根据前面的例子,同样可以归纳出它的递归模式如下:
bubble一个元素为N的数组就是:
对第一个元素(以及它后续的那个元素)进行一次比较和交换(compareAndSwitch),
然后对余下的N-1个元素递归地进行bubble。
比较与交换同样的先用一个抽象的过程表示,据此,得出代码如下(同样省略了base case):
private static void bubble(int bn, int n, int[] array) {
if (bn > 1) {
compareAndSwitch(bn, n, array);
bubble(bn - 1, n, array);
}
}
private static void compareAndSwitch(int bn, int n, int[] array) {
// TODO
}
你会发现这里的bubble与前面的bubbleSort在形式上是非常像的。
有些人可能会在bn或者n的实际含义上纠结,总是忍不住把它们往array的index上去想,这实际上还是没能摆脱往具体实现层面上去思考的惯性。我们应该抽象地去思考,不要老惦记着array,其实关键就在于要表达清楚我们的意思,这样就行了。
我们最终肯定要处理index的问题,但目前还不是时候,你应该坚信index肯定能用bn及n表达出来,你只需往下传递它们就是了。
比较与交换
现在终于要处理让我们有点头痛的index问题了。
我们只需考察最简单的两个元素第一次比较的情况,此时n=2,bn=2,我们要比较array[0],array[1],显然0=n-bn,也即是要比较array[n-bn]和array[n-bn+1]。
最终结果如下:
private static void compareAndSwitch(int bn, int n, int[] array) {
int index = n - bn;
if (array[index] > array[index + 1]) {
int temp = array[index];
array[index] = array[index + 1];
array[index + 1] = temp;
}
}
你可能有点怀疑,这样就正确了吗?我们可以实际测试一下即可,通常八九不离十。
改进
如果一轮bubble没有发生任何交换,意味着数组已经是有序的了,可以提前break。可以引入一个boolean来达到这一点,这里就不演示了。最终的代码如下:
// 对外接口
public static void sort(int[] array) {
if (array != null && array.length > 1) {
bubbleSort(array.length, array);
}
}
// 具体内部实现
private static void bubbleSort(int n, int[] array) {
if (n > 1) {
bubble(n, n, array);
bubbleSort(n - 1, array);
}
}
// 冒泡
private static void bubble(int bn, int n, int[] array) {
if (bn > 1) {
compareAndSwitch(bn, n, array);
bubble(bn - 1, n, array);
}
}
// 比较与交换
private static void compareAndSwitch(int bn, int n, int[] array) {
int index = n - bn;
if (array[index] > array[index + 1]) {
int temp = array[index];
array[index] = array[index + 1];
array[index + 1] = temp;
}
}
总结
其实写递归程序的套路经常是比较固定的,大的方面就是一个if else,递归部分可以放if,也可以放在else,就看if条件是如何判断了。然后就是找出递归模式,把条件填充上去。暂时不明朗的地方,可以先用一个抽象来表达,然后逐步地把细节完善。
对递归程序而言,通常一旦正确了,它就是正确的。
当然,这好像是一句废话。为什么这么说呢?要知道正确的方式通常只有一种,而错误的方式则有千万种。
俄国有位师太(叫托尔斯泰),在他的《安娜·卡列妮娜》中曾经曰过:“幸福的家庭总是相似的,不幸的家庭各有各的不幸。”
'All happy families are alike; each unhappy family is unhappy in its own way.'--Leo Tolstoy Anna Karenina
所以,这里真正想表达的意思是,递归式通常更为精练,没有过多枝枝蔓蔓的东西。它的环节比较少,过程式的东西较少,写法通常也很固定,因而减少了你犯错的机会。你只要找准了终止条件和递归模式,它通常就自然而然的正确了。
另外则是要强调抽象的思考问题,不要过早地陷于具体实现及细节的纠缠中,而是要一步步地最终使得一切水落石出。
当然,就这个例子而言,比起普通循环而言,并没有什么优势。
递归反而可能显得有点拖沓,这里不过是想说明普通循环能解决的问题也能用递归来解决;
另一方面,如果还不习惯于递归式的表达,恐怕写起来比普通循环更费劲;
此外,除非是简单小量的排序,否则性能也是个问题。
在下一篇章中,将探讨一个更加复杂的例子,也即是前面提到的求换零钱种数的问题,那时才能体现出递归的优势来。