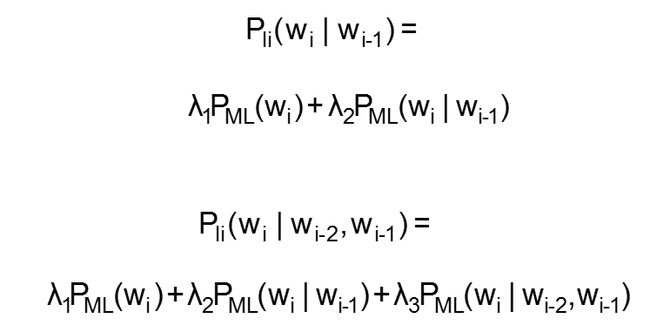搜索引擎之N元分词方法
香农游戏(Shannon Game)
根据前面的(n-1)个词预测下一个单词可能是什么?
“NBA______”
比赛? 球星? 篮球?秀选?
“直播NBA______”
决赛?季后赛?
转移概率P(比赛|NBA)
选择n值
词汇量(V) = 20,000
可靠性(Reliability)和可区别性(Discrimination)成反比,需要折中
n越大,区别力越大;n越小,可靠性越高
N取多大?
理论上讲,越大越好
经验值:二元或三元(trigram)
二元模型
如果简化成一个词的出现仅依赖于它前面出现的一个词,那么就称为二元模型(bigram)。
即:
P(S) = P(w1,w2,...,wn)= P(w1) P(w2|w1) P(w3|w1,w2)…P(wn|w1w2,...,wn-1)
≈P(w1) P(w2|w1)P(w3|w2)…P(wn|wn-1)
基本的计算方法:
P(wi|wi-1) ≈ freq(wi-1,wi) /freq(wi-1)
二元搭配词典
Freq(有,意见)=4
P(意见|有) ≈ freq(wi-1,wi) /freq(有)=4/4000=0.001
因为数据稀疏导致 “意见,分歧” 等其他的搭配都没找到。
P(S1)和P(S2)都将是0,无法通过比较计算结果找到更好的切分方案。
这就是零概率问题。
查找二元词典
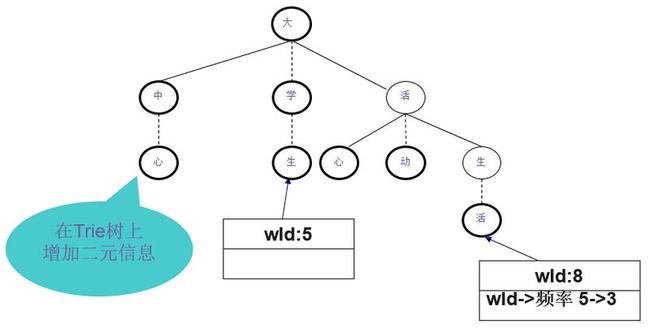
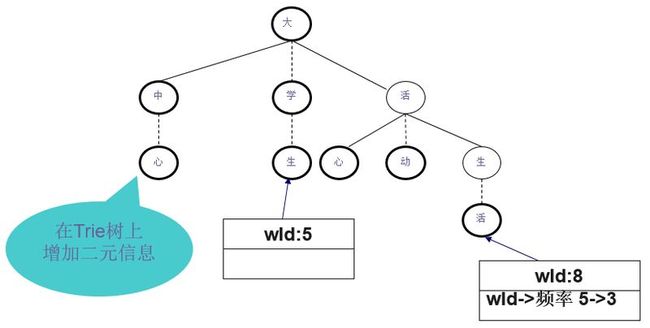
可以采用Trie树的形式来存放N元模型的参数。与词典Trie树的区别在于:词典Trie树上每个结点对应一个汉字,而N元模型Trie树的一个结点对应一个词。
或者可以把搭配信息存放在词典Trie树的叶子节点上。每个词有一个编号wId。
public class BigramMap {
public int[] keys;//词编号
public int[] vals;//频率
}
以存储“大学生,生活”为例,“生活”的词编号是8,大学生的词编号是5。假设“大学生,生活”频率是3

避免零概率:数据平滑(smoothing)
p’(w) ≈p(w), 但p’(w)≠0
对一些p(w)>0,生成p’(w)<p(w)
分配概率D给所有概率为0的项目w: p’(w)>p(w)=0
可能对于概率值较低的词也作调整
可能有些w: p’(w)=p(w)
需要确保
有许多数据平滑的方法
加1平滑
加Lambda平滑
Witten-Bell平滑
Good-Turing平滑
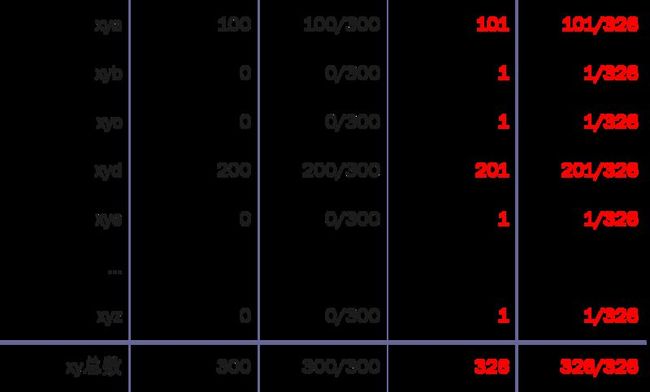
加一平滑
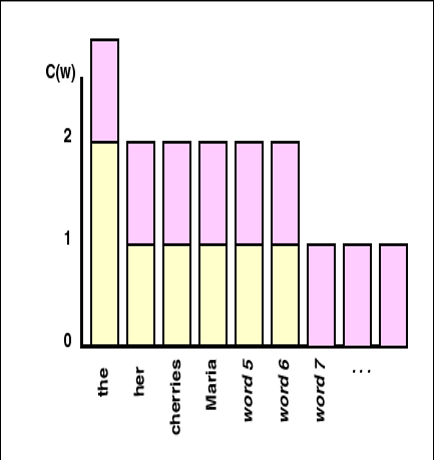
26个字母,每个都加1
300个观测事件,而不是3个,有了更好的数据后,平滑更少了
假设有20000个单词类型,而不是26个字母
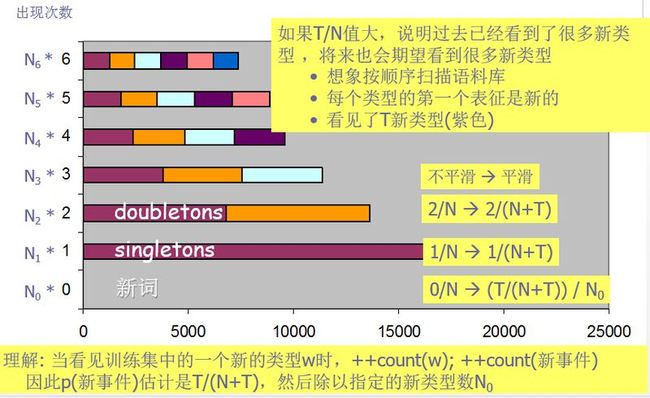
“新事件” = 零次事件(不会在训练集中出现)。
这里: 19998个新事件,全部估计概率是19998/20003.
因此加一平滑认为特别可能看到新事件,而不是在训练集已经看到的单词。
仅仅因为有一个大词典就如此认为:引入了20000个可能的事件。
“想的太多,违背直觉而出错了”?
加Lambda平滑
大的词典使得新事件变得太有可能了。
解决方法:不是加1到所有的频率上,而是加 = 0.01?
这样又可能给太小的可能性到新事件
如何选择最好的l?
也就是说,要平滑多少?
例如,分出多少概率给新事件?
依赖于新事件有多大可能出现
可能依赖于文本的类型,训练语料集的大小…
从数据中判断要平滑多少。
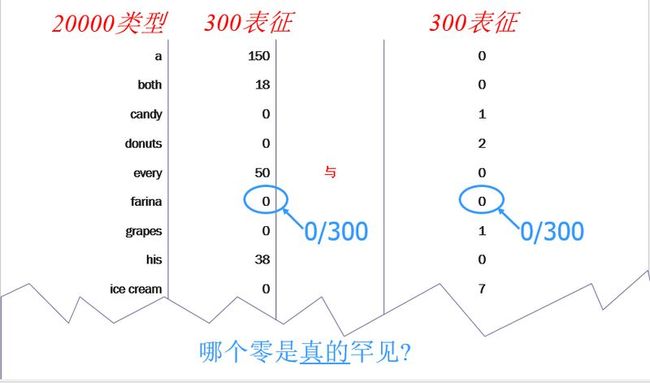
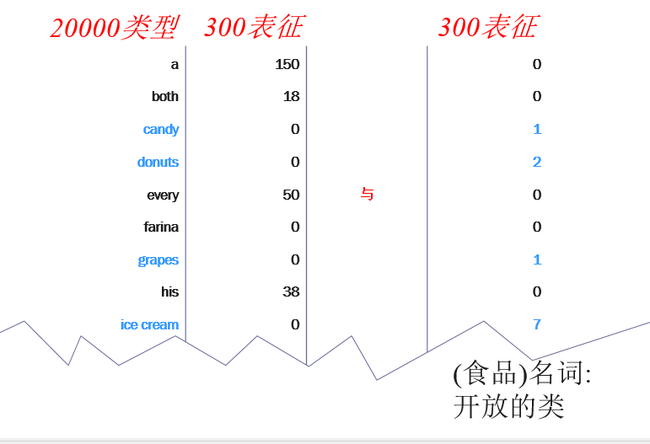
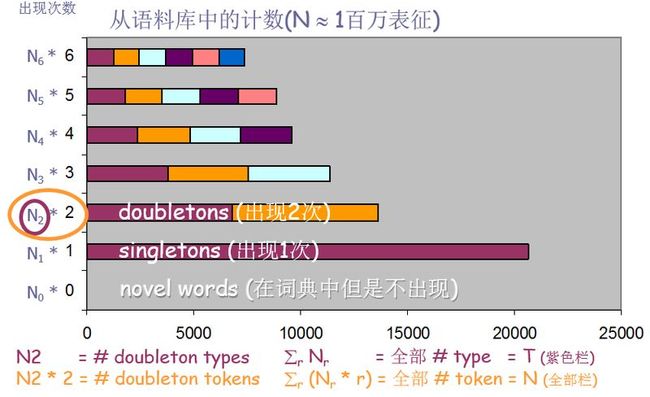
术语: 类型 与 表征
词 类型(type) = 不同的词汇项
词 表征(token) = 该类型在语料库中的出现
词典是一个类型的列表 (词典中的每一项就是一个类型)
语料库是一个表征的列表(每个类型有许多表征)
有任何理论上的好方法来选择λ?新事件有多大可能?
新事件有多常见?
Witten-Bell 平滑思想
Good-Turing平滑思想
证明Good-Turing
实验次数
通过留一个训练证明! 蓝色部分是训练集。黄色部分是留出来的一个表征。蓝色部分加黄色部分做测试集。
轮流拿出N个表征中的一个,训练集大小是N-1,拿出来的集合大小是1
不是仅仅调整l,可以调整多个值
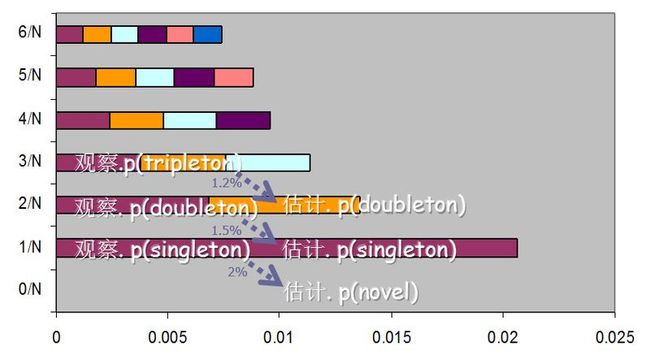
p(novel)=0.02=N1/N [=黄色部分拿出来的一个开发词在蓝色训练集里是新事件]
p(singleton)=0.015=N2*2/N [=黄色部分拿出来的一个开发词在蓝色训练集里是singleton]
p(doubleton)=0.012=N3*3/N [=黄色部分拿出来的一个开发词在蓝色训练集里是doubleton]
也就是
p(novel) = 在全部训练集里的singleton部分
p(singleton) =在全部训练集里的doubleton部分,依次类推
Witten-Bell平滑
Witten-Bell构想:如果已经看到许多不同的事件 ,则新事件也是有可能的。 (考虑 类型/表征 比率)
Good-Turing构想:如果已经看到许多singleton,则新事件也是有可能的。
Good-Turing平滑
构想:可以通过singleton的比率判断新事件的比率
假设 Nr = 出现r次的词类型数量
例如,N0 = 没看到的单词数
例如,N1 = 只出现1次的单词数
假设N = N = S r Nr = 总的词数
朴素的估计:如果x有r个表征,则 p(x) = ?
答案: r/N
全部的朴素概率全部的有r个表征的词类型?
答案: : Nr r / N
这个全部概率的Good-Turing 估计:
定义成: Nr+1 (r+1) / N
主要思想:利用高频n-gram的频率调整低频n-gram的频率。估计次数r*:
问题:有1个n-gram出现了r=1000次,有0个n-gram出现了1001次,那么,
解决方法:可以把概率最大的词保持原概率不变,但仍然参与归一化处理
Good Turing平滑的例子
想象正在钓鱼
已经钓到了10条鲤鱼,3条鳕鱼,2条金枪鱼,1条鳟鱼,1条三文鱼,1条鳗鱼。
多大可能下一条是新的一种鱼?
3/18
多大可能下一条是金枪鱼?
小于 2/18
简单线性插值(Simple Linear Interpolation)
这里 λ1 +λ2 +λ3 =1,而且对所有的i来说,λi≥0
线性插值
这个估计定义了分布:
估计条件概率
使用Good Turing估计条件概率
例如,估计三元连接条件概率:
根据平滑公式计算举例
P(S1) = P(有) * P’(意见|有) * P’(分歧|意见)
= P(有) * (0.3P(意见)+0.7P(意见|有)) * (0.3P(分歧)+0.7P(分歧|意见) )
= 0.0180*(0.3*0.001+0.7*0.001)*(0.3*0.0001)
= 5.4*10-9
P(S2) = P(有意) * P’(见) * P’(分歧)
= P(有意) * (0.3P(见)+0.7P(见|有意)) * (0.3P(分歧)+0.7P(分歧|见) )
= 0.0005*(0.3*0.0002) *(0.3*0.0001)
= 9*10-13
P(S1)> P(S2)
动态规划求解二元模型
到Nodei为止的最大概率称为Nodei的概率。
如果Wj的结束节点是Nodei,就称Wj为Nodei的前驱词
这里的prev2(Nodei)就是节点i的二级前驱词序列,记做Wj,Wk 。
比如上面的例子中,“意见”和“见”都是节点3的1级前驱词,候选词“有”就是节点3的2级前驱词。
StartNode(wj)是wj 的开始节点,也是节点i的2级前驱节点。
因此切分的最大概率max(P(S))就是P(Nodem)也就是
P(节点m的最佳2级前驱节点)*P(节点m的2级最佳前驱词序列)
求解二元模型的实现
//计算节点i的最佳前驱节点
void getBestPrev(AdjList g,int i){
Iterator<CnToken> it1 = g.getPrev(i);//得到一级前驱词集合
double maxProb = Double.NEGATIVE_INFINITY;
int maxPrev1 = -1;
int maxPrev2 = -1;
while(it1.hasNext()) {
CnToken t1 = it1.next();
Iterator<CnToken> it2 = g.getPrev(t1.start);//得到一级前驱词对应的二级前驱词集合
while(it2.hasNext()){
CnToken t2 = it1.next();
int bigramFreq=getBigramFreq(t2,t1);//从二元词典找二元频率
double biProb = lambda1*t1.freq + lambda2*(bigramFreq/t2.freq);//平滑后的二元概率
double nodeProb = prob[t2.start]+(Math.log(biProb));
if (nodeProb > maxProb)//概率最大的算作最佳前趋
{
maxPrev1 = t1.start;
maxPrev2 = t2.start;
maxProb = nodeProb;
}
}
}
prob[i] = maxProb;
prev1Node[i] = maxPrev1;
prev2Node[i] = maxPrev2;
}
N元模型扩展
可以用于汉字(字符)的搭配关系:
“张志___”
强? 刚?杰?
“汪___”
洋? 涵?溪?