【程序猿笔试面试解题指南】链表问题汇总

链表作为一种较为简单的数据结构，经常出现在各个公司的笔试面试题中。我们先看一下链表的定义:

链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间，而顺序表相应的时间复杂度分别是O(logn)和O(1)。wiki

链表是线性表，也就是有单一前驱和单一后继。而链表简单的可以分成单向和双向链表：

单向链表除去data域只有一个指向后继节点的指针；双向链表中节点有两个指针，一个指向前驱，一个指向后继。

题型1:

给你一个单向链表的头节点，找到倒数第k个节点。

解题:

由于单向链表你不知道它的长度，朴素的做法是:第一次利用一个指针遍历整个链表得到长度n，第二次利用计数器count:

for(int count=0;count<n-k;count++)
{
// point=point->next;
}

这样我们差不多遍历了两次链表，那么能不能只遍历一次链表呢？

当然能，使用两个指针即可。（设这两个指针为p1,p2）

策略是：开始时p1=p2=head。让p1先走k步，然后再让p1,p2一起走，这样p1就比p2快了k步，当p1到达链表尾部时，p2正好指向倒数第k个节点。

p1=p2=head;
for(int count=0;count<k;++count)
{
    p1=p1->next;
}
while(p1)
{
    p1=p1->next;
    p2=p2->next;
}

这题还有一些变种:

找到单向链表的中分点（1/2处）。

也是利用p1,p2，只不过这次策略是:p1每走两步，p2走一步，这样p1到链表尾部时p2在1/2处。

p1=p2=head;
while(p1)
{
    p1=p1->next;
    p1=p1->next;
    p2=p2->next;
}

依此类推，找到单向链表1/n处。

p1=p2=head;
while(p1)
{
    for(int i=0;i<n;i++)
        p1=p1->next;
    p2=p2->next;
}

题型2:

如何判断一个链表有环。

解题:

利用上题的方针，我们利用两个指针p1,p2，使其步进不同，如果链表有环，他们一定会相遇在环上的某点。

p1=p2=head;
while(p1!=p2)
{
    p1=p1->next;
    p1=p1->next;
    p2=p2->next;
}

题型3:

如何判断两个链表相交（假设无环）。

解题:

朴素的做法是：我们只要在两个链表中各找到一个节点，如果两个节点相等，也即是相交。这样的算法复杂度是:O(n*m)。（n,m为两个链表长度）

而更聪明的做法是:

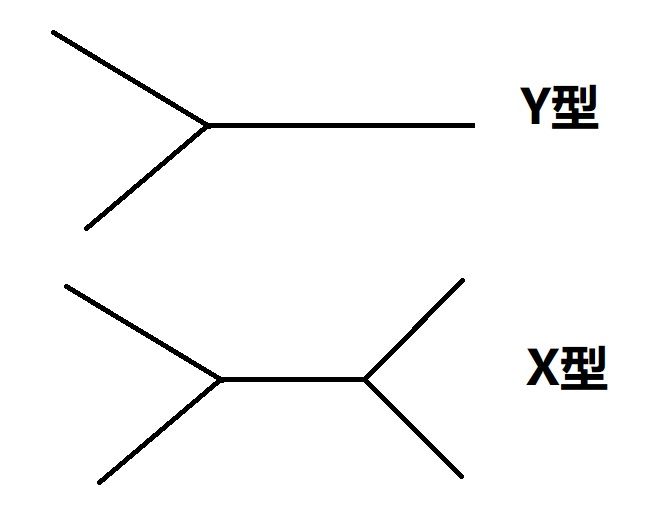
首选我们要知道，链表相交必须是Y型而不可能是X型。

因为链表只有单一后继，而X型的话，会有一个节点后两个后继。所以，只要找到两个链表链表尾，比较是否相等即可。

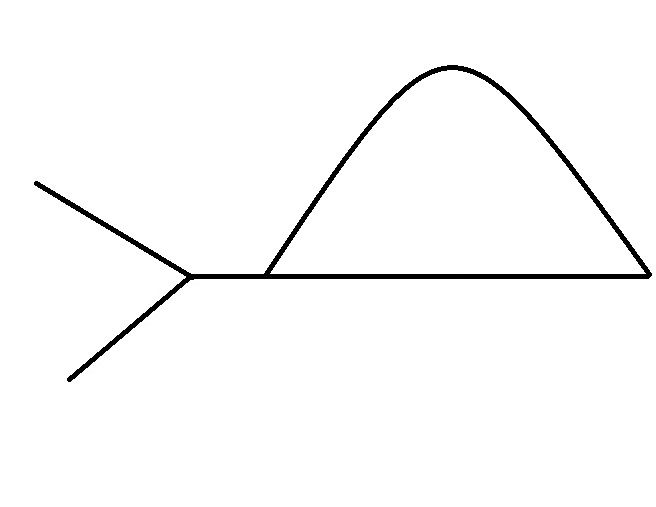
变种:假设链表有环。

这样的话，我们就无法找到链表尾了。而两个相交有环的链表一定是下图所示:

回想我们在判断链表有环的策略，如果让p1=a.head,p2=b.head(a,b为两链表头指针)，再利用不同步进，如果p1,p2相遇，链表相交。

p1=a.head;p2=b.head;
while(p1!=p2)
{
    p1=p1->next;
    p1=p1->next;
    p2=p2->next;
}

题型4:

两链表相交，找到它们的第一个共同节点。(假设无环)。

解题:

同样的，最naive的做法是:两个指针p1,p2分别指向两链表表头（p1=a.head,p2=b.head），对每个p1，遍历链表b,直到找到p2=p1。--算法复杂度为:O(n*m)

精明的做法是:

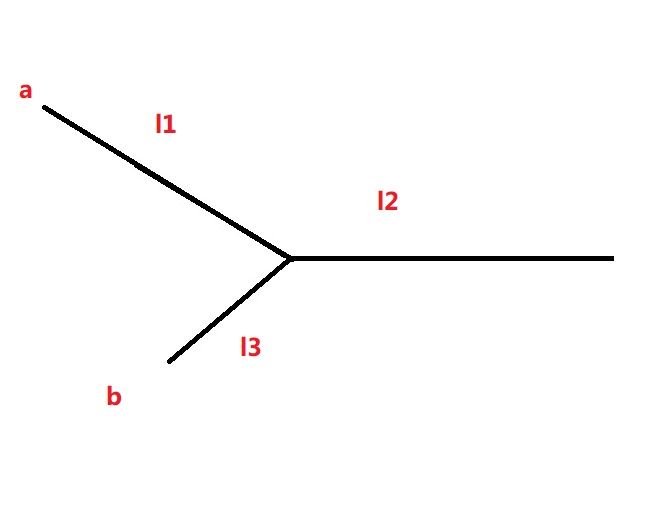
我们已经知道无环相交的两链表是Y型的。

a的长度n=l1+l2,b的长度m=l3+l2

这样n-m=l1-l3,利用题型1的策略:

指针p1=a.head,p2=b.head,p1比p2先行k=n-m步，再两者同一步进，则第一个p1=p2处就是第一个公共节点。

p1=a.head;p2=b.head;
int n,m;
while(p1)
{
    p1=p1->next;
    n++;
}
while(p2)
{
    p2=p2->next;
    m++;
}
int k=n-m;
p1=a.head;
p2=b.head;
if(k>0)
{
        for(int i=0;i<k;i++)
            p1=p1->next;
        while(p1!=p2)
        {
            p1++;
            p2++;
        }
}
else
{
        k=0-k;
        for(int i=0;i<k;i++)
            p2=p2->next;
        while(p1!=p2)
        {
            p1++;
            p2++;
        }
}

变种:两链表相交，找到它们的第一个共同节点。(假设有环)

同样，先看图:

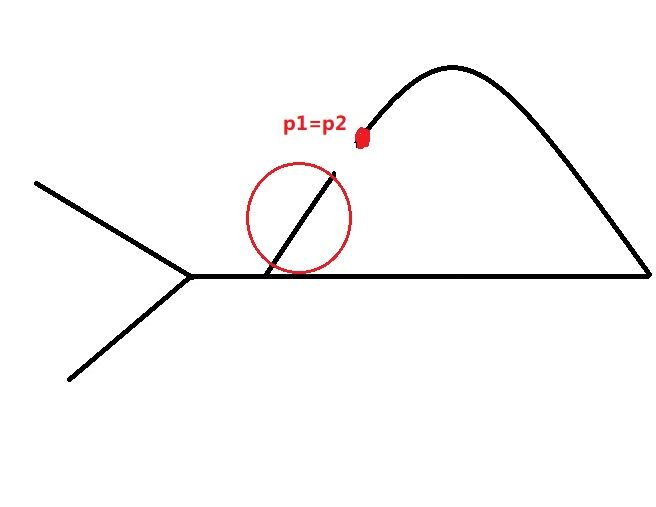
先利用题型3变种"如何判断两个链表相交（假设有环）"的方式找到环上一点p1=p1处。我们从这里将环分开，于是图形变换为:

图示其实这时候两链表又恢复成Y型，图中圆圈部分由于没了前驱也就无法被遍历，在与不在没有区别。这时候我们再利用“两链表相交，找到它们的第一个共同节点。(假设无环)。”的方法也就能解答，但是，其实断开链表这种操作知识为了形象，我们需要的仅是两链表长度的差值。于是:

p1=a.head;p2=b.head;
int n=0,m=0;
while(p1!=p2)
{
    p1=p1->next->next;
    p2=p2->next;
    n=n+2;
    m++;
}
int k=n-m;
p1=a.head;
p2=b.head;
if(k>0)
{
        for(int i=0;i<k;i++)
            p1=p1->next;
        while(p1!=p2)
        {
            p1++;
            p2++;
        }
}
else
{
        k=0-k;
        for(int i=0;i<k;i++)
            p2=p2->next;
        while(p1!=p2)
        {
            p1++;
            p2++;
        }
}

题型5:

给定一个单向链表和一个指向链表节点的指针，删除这个节点。

解题:

将这个指针设为p，删除这个节点我们需要将q的前驱q的next指针指向p的后继，即:

q->next=q->next;

可是由于单向链表我们找到p的前驱需要从头开始遍历链表，算法复杂度为:O(n)

这样显然是不够好的，我们有把握去做到O(1)

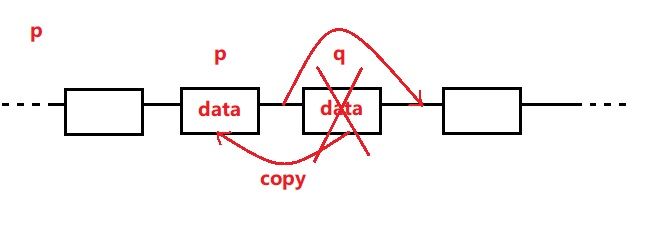
方法是:我们将p->next节点的数据复制到p上，再删除p->next这个节点而非p，这样只需O(1)便可以。

q=p->next;
//copy data from q to p
p->next=q->next;
delete q;

算法图示:

可是，这样带来一个问题:要是p是尾节点，那么p->next也即是NULL，NULL->next明显会引起错误。所以，当p为尾节点时，一老一实的使用O(n)的办法吧。这样下来，算法复杂度为:((n-1)/n)*O(1)+(1/n)*O(n)=O(1).

最后，免责说明：

本人对文章的准确性专业性权威性不负任何责任，望各位睁大眼睛自己甄别，如有错误或更好的见解请在评论中指出，谢谢！