二分匹配题集
普通匹配,多重匹配
【HDU】
1068 Girls and Boys 最大匹配★
1150 Machine Schedule 最小点覆盖★
1151 Air Raid 最小路径覆盖★
1179 Ollivanders 最大匹配★
1281 棋盘游戏 行列匹配+求关键点★★
1498 50 years, 50 colors 行列匹配★
1507 Uncle Tom's Inherited Land* 黑白染色+奇偶匹配(1X2的矩形覆盖)★
1528 Card Game Cheater 最大匹配★
1845 Jimmy’s Assignment 最大匹配(HK算法)★
2063 过山车 最大匹配★
2119 Matrix 行列匹配
2444 The Accomodation of Students 并查集分集合+最大匹配(好题!)★★
2768 Cat vs. Dog 最大独立集★★
3360 National Treasures 黑白染色+最小点覆盖★★
1045 Fire Net 行列匹配变形★★
1350 Taxi Cab Scheme 最小路径覆盖★
3118 Arbiter 枚举二分图(好题!)★★★
3729 I'm Telling the Truth最大匹配+输出字典序最大的匹配情况★★
2389 Rain on your Parade 最大匹配(HK算法)★★
1054 Strategic Game 最小点覆盖★
2819 Swap 行列匹配+输出解★★
1669 Jamie's Contact Groups 二分+多重匹配★★
3605 Escape 多重匹配★
3861 The King’s Problem 强连通+最小路径覆盖★★
2236 无题II 二分+二分匹配★★
1083 Courses 最大匹配★
1526 A Plug for UNIX 最大匹配★
2458 Kindergarten 行列匹配★
4160 Dolls 最大匹配★
4185 Oil Skimming 黑白匹配★
2413 Against Mammoths 二分+二分匹配★★
3468 Treasure Hunting 最短路+二分匹配★★★
3517 Adopt or not 最大独立集★★★
3026 Chinese Chess 二分匹配必须边★★★
===============================================================================================
【POJ】
1087 A Plug for UNIX
1274 The Perfect Stall
1469 COURSES
1486 Sorting Slides 二分图的必须边
1548 Robots
1698 Alice's Chance
1719 Shooting Contest
2060 Taxi Cab Scheme 最小路径覆盖
2112 Optimal Milking 二分+多重匹配
2226 Muddy Fields 行列的覆盖
2239 Selecting Courses
2289 Jamie's Contact Groups 二分+多重匹配
2446 Chessboard
2536 Gopher II
2584 T-Shirt Gumbo
2594 Treasure Exploration 可相交最小路径覆盖
2672 Hotkeys
2724 Purifying Machine
3020 Antenna Placement
3041 Asteroids 简单行列匹配
3189 Steady Cow Assignment 二分+多重匹配
3216 Repairing Company
3343 Against Mammoths
3692 Kindergarten
2771 最大独立集
一些概念:
匹配:
给定一个二分图,在G的一个子图G’中,如果G’的边集中的任意两条边都不依附于同一个顶点,则称G’的边集为G的一个匹配
最大匹配:
在所有的匹配中,边数最多的那个匹配就是二分图的最大匹配了
顶点覆盖:
在顶点集合中,选取一部分顶点,这些顶点能够把所有的边都覆盖了。这些点就是顶点覆盖集
最小顶点覆盖:
在所有的顶点覆盖集中,顶点数最小的那个叫最小顶点集合。
独立集:
在所有的顶点中选取一些顶点,这些顶点两两之间没有连线,这些点就叫独立集
最大独立集:
在左右的独立集中,顶点数最多的那个集合
路径覆盖:
在图中找一些路径,这些路径覆盖图中所有的顶点,每个顶点都只与一条路径相关联。
最小路径覆盖:
在所有的路径覆盖中,路径个数最小的就是最小路径覆盖了。
下面给出二分图中两个公式的证明:
1. 最小点集覆盖 = 最大匹配
König定理是一个二分图中很重要的定理,它的意思是,一个二分图中的最大匹配数等于这个图中的最小点覆盖数。如果你还不知道什么是最小点覆盖,我也在这里说一下:假如选了一个点就相当于覆盖了以它为端点的所有边,你需要选择最少的点来覆盖所有的边。比如,下面这个图中的最大匹配和最小点覆盖已分别用蓝色和红色标注。它们都等于3。这个定理相信大多数人都知道,但是网络上给出的证明并不多见。有一些网上常见的“证明”明显是错误的。因此,我在这里写一下这个定理的证明,希望对大家有所帮助。
假如我们已经通过匈牙利算法求出了最大匹配(假设它等于M),下面给出的方法可以告诉我们,选哪M个点可以覆盖所有的边。
匈牙利算法需要我们从右边的某个没有匹配的点,走出一条使得“一条没被匹配、一条已经匹配过,再下一条又没匹配这样交替地出现”的路(交错轨,增广路)。但是,现在我们已经找到了最大匹配,已经不存在这样的路了。换句话说,我们能寻找到很多可能的增广路,但最后都以找不到“终点是还没有匹配过的点”而失败。我们给所有这样的点打上记号:从右边的所有没有匹配过的点出发,按照增广路的“交替出现”的要求可以走到的所有点(最后走出的路径是很多条不完整的增广路)。那么这些点组成了最小覆盖点集:右边所有没有打上记号的点,加上左边已经有记号的点。看图,右图中展示了两条这样的路径,标记了一共6个点(用 “√”表示)。那么,用红色圈起来的三个点就是我们的最小覆盖点集。
首先,为什么这样得到的点集点的个数恰好有M个呢?答案很简单,因为每个点都是某个匹配边的其中一个端点。如果右边的哪个点是没有匹配过的,那么它早就当成起点被标记了;如果左边的哪个点是没有匹配过的,那就走不到它那里去(否则就找到了一条完整的增广路)。而一个匹配边又不可能左端点是标记了的,同时右端点是没标记的(不然的话右边的点就可以经过这条边到达了)。因此,最后我们圈起来的点与匹配边一一对应。
其次,为什么这样得到的点集可以覆盖所有的边呢?答案同样简单。不可能存在某一条边,它的左端点是没有标记的,而右端点是有标记的。原因如下:如果这条边不属于我们的匹配边,那么左端点就可以通过这条边到达(从而得到标记);如果这条边属于我们的匹配边,那么右端点不可能是一条路径的起点,于是它的标记只能是从这条边的左端点过来的(想想匹配的定义),左端点就应该有标记。
最后,为什么这是最小的点覆盖集呢?这当然是最小的,不可能有比M还小的点覆盖集了,因为要覆盖这M条匹配边至少就需要M个点(再次回到匹配的定义)。
证完了。
2. DAG的最小路径覆盖数=DAG图中的节点数-相应二分图中的最大匹配数.
证明: DAG的最小路径覆盖是指找最小数目的互相不相交的有向路径,满足DAG的所有顶点都被覆盖.
那么对应一个DAG,如何构造相应的二分图?对于DAG中的一个顶点p,二分图中有两个顶点p和p',对应DAG中的一条有向边p->q,二分图中有p-q'的一条边。二分图中p属于S集合,p'属于T集合。
下面我们来解释上面公式为什么成立,思路参考baihacker神牛:
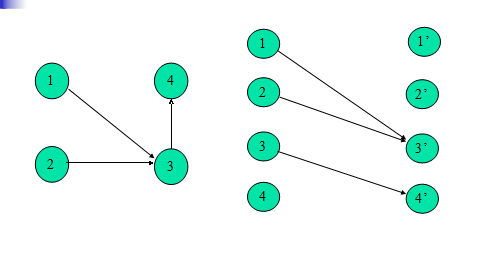
上图中,对应左边的DAG建立构造右边的二分图,可以找到二分图的一个最大匹配M:1-3',3-4',那么M中的这两条匹配边怎样对应DAG中的路径的边?
使二分图中一条边对应DAG中的一条有向边,1-3'对应DAG图中的有向边1->3,这样DAG中1就会有一个后继顶点(3会是1的唯一后继,因为二分图中一个顶点至多关联一条边!),所以1不会成为DAG中 一条路径中的结尾顶点,同样,3-4'对应DAG中3->4,3也不会成为结尾顶点,那么原图中总共4个顶点,,减去2个有后继的顶点,就剩下没有后继的顶点,即DAG路径的结尾顶点,而每个结尾顶点正好对应DAG中的一条路径,二分图中寻找最大匹配M,就是找到了对应DAG中的非路径结尾顶点的最大数目,那么DAG中顶点数-|M|就是DAG中结尾顶点的最小数目,即DAG的最小路径覆盖数。
题集转自:http://blog.csdn.net/shahdza/article/details/7779312
定义术语转自:http://blog.sina.com.cn/s/blog_89a06c7d0100trcg.html
最小点集覆盖证明转自:http://www.matrix67.com/blog/archives/116
最小路径覆盖证明转自:http://www.cnblogs.com/jackiesteed/articles/2043934.html