一种光栅绘制直线的方法

声明：本篇文章不得转载，如需转载必须经过作者同意。否则，将予追究。

最近《图形学》已经学习了光栅绘制直线的两种算法：DDA算法和中点画线算法。

在老师刚刚介绍光栅绘制直线算法时，我在课堂上就想着一个问题，这个问题使我无法好好听课，因此走了神。但还好，DDA算法很容易理解，回家自己看看书就明白了，其实就是用增量来绘制直线的。我想的这个问题就是：通过确定一条直线的起始点A(xs,ys)和终止点B(xe,ye)，可以算出其中点M(xm,ym)，绘制中点M。然后再通过同样的过程将AM和MB分别作为一条直线，并计算出其中点并绘制，如图：

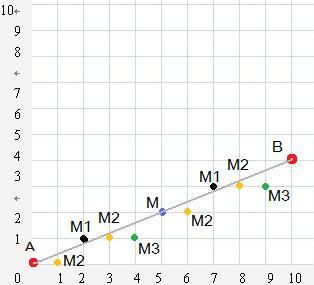
1.绘制起始点A，B；
2.计算出AB中点M，绘制M；
3.计算出AM中点M1和MB中点M1，并绘制M1；
4.重复这个过程，知道当直线两点相减为1.

实现这个算法有一个问题：如此多的中点似乎是成2的次方增长，如何确定计算并绘制这些中点呢？
曾经看过一本C语言抽象思想的书籍，介绍的是递归算法，虽然当时有些不通，但此时不妨试一试。一试，成了。
经过测试，在增量x和增量y相等的时候，可以绘制出非常完美的直线；其他情况有两种但并未深入研究，只能在此说明一下直线的情况。一种直线成散点状态，一种直线并不十分直。源代码如下：

 1  /*
 2      Title: Another Method for Drawing Line
 3      Author: Wulei
 4      Date: 2008-10-16
 5  */
 6  #include < graphics.h >
 7 
 8  void  Method( int  xs,  int  ys,  int  xe,  int  ye);
 9 
10  main()
11  {
12       int  gd = DETECT,gm;
13      initgraph( & gd, & gm, "" );
14 
15      Method( 0 , 0 , 100 , 100 );
16      getch();
17      closegraph();
18  }
19 
20  /*  Wulei's Method for Drawing Line  */
21  void  Method( int  xs,  int  ys,  int  xe,  int  ye)
22  {
23      int  xm, ym;
24     xm  =  (xs  +  xe)  /   2 ;
25     ym  =  (ys  +  ye)  /   2 ;
26      if ( xm  ==  xs  &&  xe  -  xs  >  ye  -  ys )
27         return ;
28      if ( ym  ==  ys  &&  xe  -  xs  <=  ye  -  ys )
29         return ;
30     putpixel( xm, ym, WHITE );
31     Method( xs, ys, xm, ym );
32     Method( xm, ym, xe, ye );
33  }

 

 声明：本篇文章不得转载，如需转载必须经过作者同意。否则，将予追究。