吴昊品游戏核心算法 Round 17 —— 吴昊教你玩拼图游戏（8 puzzle）

 

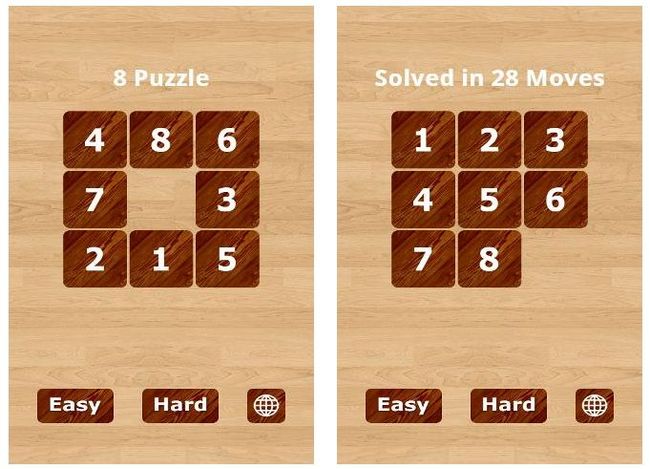
  如图所示，这是一个九宫格（这倒是让我想起了小时候老师在黑板上教导我们的如何通过一系列的拼凑，将横行，竖行，以及斜行都拼到和相等），格子中有一个格子是空的，另外八个格子分别有数字1--8，我们的任务是将原图通过空格转换为前面八格为1--8，而最后一格为空。

  以上的截图来自如下的一款android游戏（当然，由于版本的原因，样式换成了一种木板式的，更贴近于我们在现实中的“八数码游戏”），其名字叫：8--Puzzle，在其软件的启动界面中，有阐述两种游戏的模式：

 

 

  何者为难？何者为易呢？这里我们有一个可以定量化的衡量标准，也就是说，我们可以以该状态还原为目标状态（这里称为Goal-Status）所需的最小步数为一个凭据。当然，这样比较单纯，我们还可以设计出更“客观”一些的，比如，有些移动是难以想到的，而有些是很容易想到的，为每一个步数赋予一个权值，这就是一个不错的想法。

  那么，关键的问题是，我们需要设计出一个AI出来，只要给出初始的状态，我们可以通过我们的AI来得到到目标状态具体需要多少步，甚至，我们可以得到每一步的具体操作过程（这里可以用u,d,l,r分别来代表上下左右）

  AI的实现方法很多，比如：裸体的BFS（Bruce Force+BFS）,双向BFS+STL，开哈希表之后，更省时间，更牛的一些办法还有楼教主在2005年的百度之星总决赛打出的A*（该算法基于启发式，后来，百度公司在之后的比赛中就以Astar作为百度之星的象征，其来源就是楼天成的A*算法）以及其进一步的IDA*算法。在博客园中，有牛人归纳出了八数码问题的八重境界，我会在最后进行转载的。

  有人说过，没有看过该AI的人，人生不完美，也许，该问题真的比较深刻吧！

 

  我们利用X来表示这个8--PUZZLE问题的空格，当然，在Input中，可以将其归为一行（毕竟，大家都知道这是个八数码问题吧！）

 

  Input : 1 2 3 x 4 6 7 5 8

 

  对于输出来说，我们只要输出一个方向就可以了（根据方向，我们可以知道是哪一个方块在动），对于这个Input，我们所得到的Output应该是：lul

 

  Output:lul

  而对于最少的次数，我们可以根据输出中的字母的数量得到。

  首先，考虑一个问题，我们的状态总数（算上那个空格）一共为9! = 362880 种，于是，即使是最野蛮的暴力+BFS也是可以的（纯粹的暴力的话，果断还是不行的），这里给出的一种方法是暴力+BFS+queue容器+Hash表。

   Solve:

 

  1 #include <iostream>
  2 
  3  #include <cstdio>
  4 
  5  #include <cstring>
  6 
  7  #include < string>
  8 
  9  #include <algorithm>
 10 
 11  #include <cmath>
 12 
 13  #include <queue>
 14 
 15  
 16 
 17   using  namespace std;
 18 
 19  
 20 
 21   #define MAXN 363000   // 9!==326880
 22 
 23  
 24 
 25   struct node
 26 
 27  {
 28 
 29     int s[ 9]; // 当前状态
 30 
 31     int loc; // '0'的位置,即'x'的位置
 32 
 33     int stat; // 康托展开的hash值
 34 
 35     string path; // 路径
 36 
 37  };
 38 
 39  
 40 
 41   // 分别存储1--9的阶乘值
 42 
 43   int fac[]={ 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880};
 44 
 45   // 同以前一样，用一个二维数组dir[4][2]来装填方向
 46 
 47   int dir[ 4][ 2]={- 1, 0, 1, 0, 0,- 1, 0, 1};
 48 
 49   // 存储方向字符，以便在之后表明路径
 50 
 51   char index[ 5]= " udlr ";
 52 
 53   int aim= 322561; // 123456780对应的hash值
 54 
 55   string path; // 路径
 56 
 57    // 作为一种标记，遍历已经访问过的状态
 58 
 59   bool vis[MAXN];
 60 
 61   // 最初的结点
 62 
 63  node st;
 64 
 65  
 66 
 67   // 康托展开求序列的hash值
 68 
 69   int cantor( const  int *s)
 70 
 71  {
 72 
 73     int sum= 0;
 74 
 75     for( int i= 0;i< 9;i++)
 76 
 77    {
 78 
 79       int num= 0;
 80 
 81       for( int j= 0;j<i;j++)
 82 
 83         if(s[j]>s[i])
 84 
 85          num++;
 86 
 87      sum+=(num*fac[i]);
 88 
 89    }
 90 
 91     return (sum+ 1);
 92 
 93  }
 94 
 95  
 96 
 97   // 这里利用越界函数来标识是否越界
 98 
 99   bool isok( int x, int y)
100 
101  {
102 
103     if(x< 0 || x> 2 || y> 2 || y< 0)
104 
105       return  false;
106 
107     return  true;
108 
109  }
110 
111  
112 
113   bool bfs()
114 
115  {
116 
117     // 初始化vis数组，将其都标记为0
118 
119    memset(vis, 0, sizeof(vis));
120 
121     // 队列容器来装载结点
122 
123    queue<node>q;
124 
125    node cur,tmp;
126 
127     // 初始结点进入队列
128 
129    q.push(st);
130 
131    vis[st.stat]= 1;
132 
133     // 如果队列非空，那么就一直重复这个过程
134 
135     while(!q.empty())
136 
137    {
138 
139       // 将首结点取出作为当前结点
140 
141      cur=q.front();
142 
143       // 将队列剥离一个
144 
145      q.pop();
146 
147       // 得到空白方块的横坐标和纵坐标
148 
149       int x=cur.loc/ 3,y=cur.loc% 3;
150 
151       for( int i= 0;i< 4;i++)
152 
153      {
154 
155         // 从四个方向对空白位置进行搜索
156 
157         int tx=x+dir[i][ 0],ty=y+dir[i][ 1];
158 
159         // 如果越界的话，换一个方向
160 
161         if(!isok(tx,ty))
162 
163           continue;
164 
165        tmp=cur;
166 
167        tmp.loc=tx* 3+ty; // '0'移动到该位置
168 
169          // 这里，相当于交换了一个方向
170 
171        tmp.s[cur.loc]=tmp.s[tmp.loc];
172 
173        tmp.s[tmp.loc]= 0;
174 
175         // 获取这个状态的hash值
176 
177        tmp.stat=cantor(tmp.s);
178 
179         // 如果这个状态没有被遍历过的话
180 
181         if(!vis[tmp.stat])
182 
183        {
184 
185          vis[tmp.stat]= 1;
186 
187           // 修改路径，字符串可以直接在后面加
188 
189          tmp.path=cur.path+index[i];
190 
191           // 如果是正解的话
192 
193           if(tmp.stat==aim)
194 
195          {
196 
197            path=tmp.path;
198 
199             return  true;
200 
201          }
202 
203           // 如果不是最优解的话，继续入队列
204 
205          q.push(tmp);
206 
207        }
208 
209      }
210 
211    }
212 
213     return  0;
214 
215  }
216 
217  
218 
219   int main()
220 
221  {
222 
223     // 假设操作的总次数不大于256
224 
225     char buf[ 256];
226 
227     // 利用gets()函数读入一行
228 
229     while(gets(buf))
230 
231    {
232 
233       int len=strlen(buf);
234 
235       int cnt= 0;
236 
237       for( int i= 0;i<len;i++)
238 
239      {
240 
241         if(buf[i]>= ' 1 '&&buf[i]<= ' 9 ')
242 
243        {
244 
245          st.s[cnt++]=buf[i]- ' 0 ';
246 
247        }
248 
249         else  if(buf[i]== ' x ')
250 
251        {
252 
253          st.s[cnt]= 0;
254 
255           // 这里标识空白区域的具体位置
256 
257          st.loc=cnt++;
258 
259        }
260 
261      }
262 
263       // 利用cantor扩展函数得到初始状态
264 
265      st.stat=cantor(st.s);
266 
267       // 如果一开始就是目标状态的话，那么就输出空气好咯！
268 
269       if(st.stat==aim)
270 
271      {
272 
273        puts( "");
274 
275         continue;
276 
277      }
278 
279       // 广搜开始
280 
281       if(bfs())
282 
283         // 输出路径
284 
285        cout<<path<<endl;
286 
287       else
288 
289         // 输出不可解
290 
291        puts( " unsolvable ");
292 
293    }
294 
295     return  0;
296 
297  }