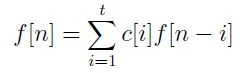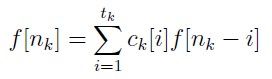hdu-4471-Homework-矩阵快速幂+优化加速
题目链接:
http://acm.hdu.edu.cn/showproblem.php?pid=4471
题目意思:
求f(n).
当n为特殊点nk时
解题思路:
当x不为特殊点时,直接用基本的矩阵快速幂,求出f[x],当x为特殊点时,用另外一个矩阵,左乘转移一下。
也就是按特殊点nk,将1-n分成很多区段,一个区段一个特殊点这样来回求。
两点优化:
1、因为要多次用到同一矩阵的快速幂,所以先预处理该矩阵的2K次幂,免的计算每个区间的时候,都要计算该矩阵的2K次幂。
2、矩阵相乘的时候,把K作为主要控制元,一次计算 a[i][k]*a[k][j] ,当有a[i][k]等于0时,直接跳出来。
注意:
矩阵大小的选取,位置的选放。
c1 c2 c3 ... ct f(n-1) f(n)
1 0 0 ... 0 f(n-2) f(n-1)
0 1 0 ... 0 f(n-3) f(n-2)
0 0 1 ... 0 ... ...
... .... ... . ... ...
0 0 0 ..1 0 f(n-t) f(n-t+1)
话不多说。
代码解释的很详细:
#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<algorithm>
#include<vector>
#include<map>
#include<set>
#include<stack>
#include<list>
#include<queue>
#define eps 1e-6
#define INF 0x1f1f1f1f
#define PI acos(-1.0)
#define ll __int64
#define lson l,m,(rt<<1)
#define rson m+1,r,(rt<<1)|1
using namespace std;
#define Maxn 110
#define M 1000000007
/*
freopen("data.in","r",stdin);
freopen("data.out","w",stdout);
*/
//本题基本思路不难想到,主要是细节优化
//学习简洁写法
struct Mar
{
int row,col;
int s[Maxn][Maxn];
void init(int a,int b)
{
row=a,col=b;
memset(s,0,sizeof(s));
}
};
Mar operator * (const Mar & a,const Mar & b)
{
Mar res;
res.init(a.row,b.col); //初始化
for(int k=1;k<=a.col;k++) //以列向量为标准,在0较多的情况下可以降低时间复杂度,
{ //以后注意这样写
for(int i=1;i<=res.row;i++)
{
if(a.s[i][k]==0)
continue;
for(int j=1;j<=res.col;j++)
{
if(b.s[k][j]==0)
continue;
res.s[i][j]=(1LL*a.s[i][k]*b.s[k][j]+res.s[i][j])%M; //枚举k时,想成可能为0
} //强制转化为ll类型,免得超了
}
}
/*
for(int i=1;i<=res.row;i++)
for(int j=1;j<=res.col;j++)
for(int k=1;k<=a.col;k++)
res.s[i][j]=(1LL*a.s[i][k]*b.s[k][j]+res.s[i][j])%M;*/
return res;
}
Mar ba,sp[Maxn],ans,pp[35]; //pp[i]表示ba^(2*i)是预处理的矩阵,免得每一次都要计算
int nn[Maxn],tt[Maxn],m,n,q,t,pos[Maxn];//对下表排序
void getpp()
{
pp[0]=ba;
for(int i=1;i<=31;i++) //10^9 最多也就2^31次方
pp[i]=pp[i-1]*pp[i-1];
}
bool cmp(int a,int b) //对下标排序,免得每次都移动,特别是单个元素内容很多时,浪费时间
{
return nn[a]<nn[b];
}
void Cal(int a)//a表示次数,矩阵快速幂算,另外一种写的形式
{
for(int i=0;i<=31;i++)
{
if(a&(1<<i))
ans=pp[i]*ans;
}
return ;
}
/*
void Cal(int a) //这样写就tle,因为每个区段都要重新算矩阵的次方,果断采用上面的那种思路
{
Mar tmp=ba;
while(a)
{
if(a&1)
ans=tmp*ans;
a=a>>1;
tmp=tmp*tmp;
}
}*/
int main()
{
int ca=0;
while(scanf("%d%d%d",&n,&m,&q)!=EOF)
{
memset(ans.s,0,sizeof(ans));
for(int i=m;i>=1;i--)
scanf("%d",&ans.s[i][1]); //开始的m个
scanf("%d",&t);
memset(ba.s,0,sizeof(ba.s));
for(int i=1;i<=t;i++) //
scanf("%d",&ba.s[1][i]);
//scanf("%d",&q);
for(int i=1;i<=q;i++)
{
pos[i]=i;
scanf("%d%d",&nn[i],&tt[i]);
memset(sp[i].s,0,sizeof(sp[i].s));
for(int j=1;j<=tt[i];j++)
scanf("%d",&sp[i].s[1][j]);
}
int Max=t;
for(int i=1;i<=q;i++)
Max=max(Max,tt[i]); //把最大的表长找到
ba.row=ba.col=Max;
ans.row=Max,ans.col=1;
for(int i=2;i<=ba.row;i++) //构造基本的矩阵
ba.s[i][i-1]=1;
getpp();
for(int i=1;i<=q;i++)
{
sp[i].row=sp[i].col=Max;
for(int j=2;j<=sp[i].row;j++) //构造特殊位置的矩阵
sp[i].s[j][j-1]=1;
}
sort(pos+1,pos+1+q,cmp); //由下标对nn排序
int last=m;
for(int i=1;i<=q;i++)
{
int p=pos[i]; //定位
if(nn[p]>n||nn[p]<=last) //不用算
continue;
Cal(nn[p]-last-1);
ans=sp[p]*ans; //特殊点单独计算
last=nn[p];
}
Cal(n-last);
printf("Case %d: %d\n",++ca,ans.s[1][1]);
}
return 0;
}