哈夫曼树及哈夫曼编码的实现(java)
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权.
哈夫曼树的构造:
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树
例:
假设一个文本文件中只包含7个字符{A,B,C,D,E,F,G},这7个字符在文本中出现的次数为{5,24,7,17,34,5,13},求这些字符的哈夫曼编码。
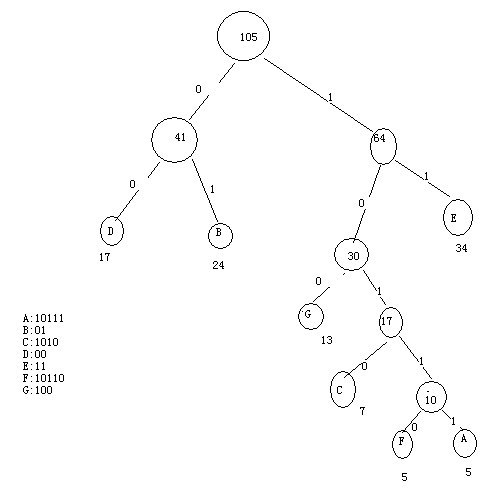
//上图的测试:
运行结果:
data:null;weight:105.0;Coding:
data:null;weight:41.0;Coding:0
data:null;weight:64.0;Coding:1
data:D;weight:17.0;Coding:00
data:B;weight:24.0;Coding:01
data:null;weight:30.0;Coding:10
data:E;weight:34.0;Coding:11
data:G;weight:13.0;Coding:100
data:null;weight:17.0;Coding:101
data:C;weight:7.0;Coding:1010
data:null;weight:10.0;Coding:1011
data:F;weight:5.0;Coding:10110
data:A;weight:5.0;Coding:10111
下载源码:
哈夫曼树的构造:
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Queue;
public class HuffmanTree<T> {
//构造哈夫曼树
public static <T> Node<T> createTree(List<Node<T>> nodes){
while(nodes.size() > 1){
Collections.sort(nodes);
Node<T> left = nodes.get(nodes.size()-1);
Node<T> right = nodes.get(nodes.size()-2);
Node<T> parent = new Node<T>(null, left.getWeight()+right.getWeight());
parent.setLeft(left);
parent.setRight(right);
nodes.remove(left);
nodes.remove(right);
nodes.add(parent);
}
return nodes.get(0);
}
//递归生成Huffman编码
public static<T> void generateHuffmanCode(Node<T> root){
if (root==null) return;
if(root.getLeft()!=null)
root.getLeft().setCoding(root.getCoding()+"0");
if(root.getRight()!=null)
root.getRight().setCoding(root.getCoding()+"1");
generateHuffmanCode(root.getLeft());
generateHuffmanCode(root.getRight());
}
public static <T> List<Node<T>> breadth(Node<T> root){ //广度优先遍历哈夫曼树
List<Node<T>> list = new ArrayList<Node<T>>();
Queue<Node<T>> queue = new ArrayDeque<Node<T>>();
if(root != null){
queue.offer(root);
}
while(!queue.isEmpty()){
list.add(queue.peek());
Node<T> node = queue.poll();
if(node.getLeft() != null){
queue.offer(node.getLeft());
}
if(node.getRight() != null){
queue.offer(node.getRight());
}
}
return list;
}
}
//哈夫曼树节点
public class Node<T> implements Comparable<Node<T>> {
private T data;
private double weight;
private String coding = ""; //哈夫曼编码
private Node<T> left;
private Node<T> right;
public Node(T data, double weight){
this.data = data;
this.weight = weight;
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public double getWeight() {
return weight;
}
public void setWeight(double weight) {
this.weight = weight;
}
public Node<T> getLeft() {
return left;
}
public void setLeft(Node<T> left) {
this.left = left;
}
public Node<T> getRight() {
return right;
}
public void setRight(Node<T> right) {
this.right = right;
}
public String getCoding(){ return coding;}
public void setCoding(String coding){ this.coding = coding;}
@Override
public String toString(){
return "data:"+this.data+";weight:"+this.weight+";Coding:"+this.coding;
}
@Override
public int compareTo(Node<T> other) {
if(other.getWeight() > this.getWeight()){
return 1;
}
if(other.getWeight() < this.getWeight()){
return -1;
}
return 0;
}
}
例:
假设一个文本文件中只包含7个字符{A,B,C,D,E,F,G},这7个字符在文本中出现的次数为{5,24,7,17,34,5,13},求这些字符的哈夫曼编码。

//上图的测试:
import java.util.ArrayList;
import java.util.List;
public class Test {
public static void main(String[] args) {
int a[]={5,24,7,17,34,5,13};
String s[]={"A","B","C","D","E","F","G"};
List<Node<String>> list1 = new ArrayList<Node<String>>();
for(int i=0;i<a.length;i++)
list1.add(new Node<String>(s[i],a[i]));
root = HuffmanTree.createTree(list1);
HuffmanTree.generateHuffmanCode(root);
List<Node<String>> list2=HuffmanTree.breadth(root);
for(Node<String> node: list2)
System.out.println(node);
}
}
运行结果:
data:null;weight:105.0;Coding:
data:null;weight:41.0;Coding:0
data:null;weight:64.0;Coding:1
data:D;weight:17.0;Coding:00
data:B;weight:24.0;Coding:01
data:null;weight:30.0;Coding:10
data:E;weight:34.0;Coding:11
data:G;weight:13.0;Coding:100
data:null;weight:17.0;Coding:101
data:C;weight:7.0;Coding:1010
data:null;weight:10.0;Coding:1011
data:F;weight:5.0;Coding:10110
data:A;weight:5.0;Coding:10111
下载源码: