图的概义及存储方法
一、概念。
图: 是一种复杂的非线性数据结构。
图的二元组定义:
图G由两个集合V和E组成,记为:
G=(V, E) 其中: V 是顶点的有穷非空集合,
E是V中顶点偶对(称为边)的有穷集。
通常,也将图G的顶点集和边集分别记为V(G)和E(G) 。 E(G)可以是空集。若E(G)为空,则图G只有顶点而没有边。
有向图: 若图G中的每条边都是有方向的,则称G为有向图 (Digraph) 。
无向图: 若图G中的每条边都是没有方向的,则称G为无向图 (Undigraph) 。
完全图: 若无向图中的每个顶点之间存在着一条边,有向图中的每两个定点之间都存在着方向相反的两条边,则称此图为完全图。
邻接点:
有向图:如果<u, v>∈E, 则称v为u的邻接点,u为v的逆邻接点。边<u, v>与顶点u和v相关联,从u出发的边称为u的出边或邻接边,而指向顶点u的边称为u的入边或逆邻接边。
无向图:如果(u, v)∈E, 则称u与v互为邻接点。
顶点的度、入度与出度:
依附与某顶点v的边数称为度;
在有向图中,顶点v的入度指以顶点为终点的边的数目。出度指以顶点为起始点的边的数目;
连通图:无向图中,若一个顶点到另一个顶点有路径,则称这2个顶点是连通的。如果图中任意2顶点都是连通的,则称该图是连通图。
连通分量:指无向图的极大连通子图。
权:与图中边有关的实数。
带权图或网:边上具有权值的图。
二、抽象数据类型
ADT Graph{
数据对象D:具有相同性质的数据元素的集合。
数据关系R:R{<u,v>|(u,v∈D)}。
基本操作:
1 int getType();//返回图的类型
2 int getVexNum();//返回图的顶点数
3 int getEdgeNum();//返回图的边数
4 Iterator getVertex();//返回图的所有顶点
5 Iterator getEdge();//返回图的所有边
6 void remove(Vertex v);//删除一个顶点v
7 void remove(Edge e);//删除一条边e
8 Vertex insert(Vertex v);//添加一个顶点v
9 Edge insert(Edge e);//添加一条边e
10 //对图进行深度优先遍历
11 //对图进行广度优先遍历
12 //求顶点v到其他顶点的最短路径
。。。。。。。。。。。。。。。。。。。。。。
}
三、图的存储方法
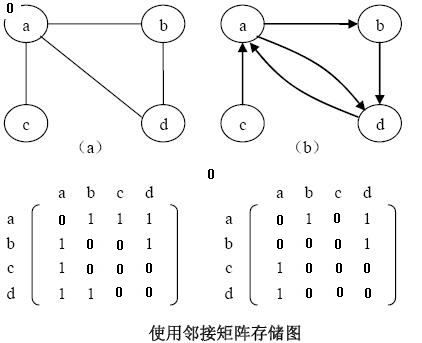
1、邻接矩阵表示法:采用2个数组来表示图;一个是存储所有顶点信息的一维数组、一个是存储图中顶点之间关联关系的二维数组,这个二维数组称为邻接矩阵
对于无向图a,邻接矩阵是一个对称矩阵。第i行(i列)非0元素的个数正好是第i个顶点的度。
对于有向图b,第i行非0元素的个数是第i个顶点的出度、i列非0元素的个数是第i个顶点的入度。
邻接矩阵的不足:
(1)、由n个顶点构成的图中最多可以有n*n条边,但大多数情况下,边的数目远远达不到这个量级,邻接矩阵中大多数单元都是闲置的。
(2)、矩阵结构是静态的,大小N需要预先估计,然后创建N*N的矩阵,而图的规模往往是动态变化的,N估计过大会造成空间浪费,过小则造成空间不够用。
2、邻接表表示法:
链接表是图的一种动态的链式存储方法,类似于树的孩子链表表示法。
对于n个顶点、m条边的无向图,采用邻接表,需要n个表头节点和2m个边表节点。在边稀疏的情况下,要比使用邻接矩阵节省空间。
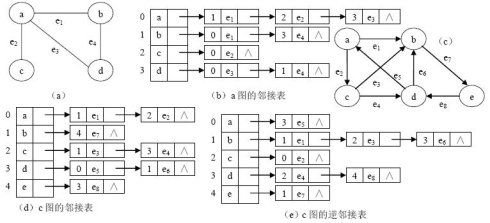
邻接表的特性:
在无向图中,顶点v的度为v的邻接表中表节点的个数。
在有向图中,顶点v的邻接表中边表的节点个数仅为v的出度。入度需要遍历这个邻接表或者从逆邻接表中获取。
判断2个顶点直接是否有边需要搜素2个顶点对应的邻接表。不如邻接矩阵方便。
图: 是一种复杂的非线性数据结构。
图的二元组定义:
图G由两个集合V和E组成,记为:
G=(V, E) 其中: V 是顶点的有穷非空集合,
E是V中顶点偶对(称为边)的有穷集。
通常,也将图G的顶点集和边集分别记为V(G)和E(G) 。 E(G)可以是空集。若E(G)为空,则图G只有顶点而没有边。
有向图: 若图G中的每条边都是有方向的,则称G为有向图 (Digraph) 。
无向图: 若图G中的每条边都是没有方向的,则称G为无向图 (Undigraph) 。
完全图: 若无向图中的每个顶点之间存在着一条边,有向图中的每两个定点之间都存在着方向相反的两条边,则称此图为完全图。
邻接点:
有向图:如果<u, v>∈E, 则称v为u的邻接点,u为v的逆邻接点。边<u, v>与顶点u和v相关联,从u出发的边称为u的出边或邻接边,而指向顶点u的边称为u的入边或逆邻接边。
无向图:如果(u, v)∈E, 则称u与v互为邻接点。
顶点的度、入度与出度:
依附与某顶点v的边数称为度;
在有向图中,顶点v的入度指以顶点为终点的边的数目。出度指以顶点为起始点的边的数目;
连通图:无向图中,若一个顶点到另一个顶点有路径,则称这2个顶点是连通的。如果图中任意2顶点都是连通的,则称该图是连通图。
连通分量:指无向图的极大连通子图。
权:与图中边有关的实数。
带权图或网:边上具有权值的图。
二、抽象数据类型
ADT Graph{
数据对象D:具有相同性质的数据元素的集合。
数据关系R:R{<u,v>|(u,v∈D)}。
基本操作:
1 int getType();//返回图的类型
2 int getVexNum();//返回图的顶点数
3 int getEdgeNum();//返回图的边数
4 Iterator getVertex();//返回图的所有顶点
5 Iterator getEdge();//返回图的所有边
6 void remove(Vertex v);//删除一个顶点v
7 void remove(Edge e);//删除一条边e
8 Vertex insert(Vertex v);//添加一个顶点v
9 Edge insert(Edge e);//添加一条边e
10 //对图进行深度优先遍历
11 //对图进行广度优先遍历
12 //求顶点v到其他顶点的最短路径
。。。。。。。。。。。。。。。。。。。。。。
}
三、图的存储方法
1、邻接矩阵表示法:采用2个数组来表示图;一个是存储所有顶点信息的一维数组、一个是存储图中顶点之间关联关系的二维数组,这个二维数组称为邻接矩阵
对于无向图a,邻接矩阵是一个对称矩阵。第i行(i列)非0元素的个数正好是第i个顶点的度。
对于有向图b,第i行非0元素的个数是第i个顶点的出度、i列非0元素的个数是第i个顶点的入度。

邻接矩阵的不足:
(1)、由n个顶点构成的图中最多可以有n*n条边,但大多数情况下,边的数目远远达不到这个量级,邻接矩阵中大多数单元都是闲置的。
(2)、矩阵结构是静态的,大小N需要预先估计,然后创建N*N的矩阵,而图的规模往往是动态变化的,N估计过大会造成空间浪费,过小则造成空间不够用。
2、邻接表表示法:
链接表是图的一种动态的链式存储方法,类似于树的孩子链表表示法。
对于n个顶点、m条边的无向图,采用邻接表,需要n个表头节点和2m个边表节点。在边稀疏的情况下,要比使用邻接矩阵节省空间。

邻接表的特性:
在无向图中,顶点v的度为v的邻接表中表节点的个数。
在有向图中,顶点v的邻接表中边表的节点个数仅为v的出度。入度需要遍历这个邻接表或者从逆邻接表中获取。
判断2个顶点直接是否有边需要搜素2个顶点对应的邻接表。不如邻接矩阵方便。