线段树入门学习(三)懒操作(兼解POJ1823) JAVA
继续上文"线段树入门学习(二)"
http://128kj.iteye.com/blog/1739064
请先看题POJ1823:
旅馆有三种操作:1入住,同时给你两个数i,M,其中i表示连续房间的起始房号,M表示房间数量;2退房,同时给你两个数i,M,其中i表示连续房间的起始房号;3查询,要求输出整个旅馆中,房号相连的最大空房间数量。
样例:
Sample Input
12 10 (房间号1 -12,有10个操作)
3
1 2 3
1 9 4
3
2 2 1
3
2 9 2
3
2 3 2
3
Sample Output
12
4
4
6
10
网上大家都用线段树来解这道题.
线段树,也叫区间树,是一个完全二叉树,它在各个节点保存一条线段,因而常用于解决数列维护问题,树的根节点表示是“整体”的区间,左右子树分别表示这个区间的左半边和右半边。
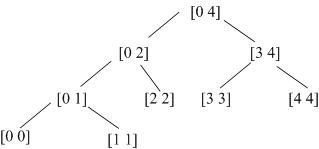
它基本能保证每个操作的复杂度为O(logN)。
当用户修改一个区间的值时,如果连同其子孙全部修改,则改动的节点数必定会远远超过O(log n)个。因而,如果要想把区间修改操作也控制在O(log n)的时间内,只修改O(log n)个节点的信息就成为必要。
以相同的方式更新某区间时,并不去真正更新其子区间,而是以某种方式把这个操作记录下来,等下一次访问到该区间并需要访问其子区间时,在访问的同时把子区间的值进行更改!这就称为懒操作。代码如下:
具体解答请看下面AC过的代码:
以上代码参考了:http://sbp810050504.blog.51cto.com/2799422/1023633
源码下载:
请先看题POJ1823:
旅馆有三种操作:1入住,同时给你两个数i,M,其中i表示连续房间的起始房号,M表示房间数量;2退房,同时给你两个数i,M,其中i表示连续房间的起始房号;3查询,要求输出整个旅馆中,房号相连的最大空房间数量。
样例:
Sample Input
12 10 (房间号1 -12,有10个操作)
3
1 2 3
1 9 4
3
2 2 1
3
2 9 2
3
2 3 2
3
Sample Output
12
4
4
6
10
网上大家都用线段树来解这道题.
线段树,也叫区间树,是一个完全二叉树,它在各个节点保存一条线段,因而常用于解决数列维护问题,树的根节点表示是“整体”的区间,左右子树分别表示这个区间的左半边和右半边。

它基本能保证每个操作的复杂度为O(logN)。
当用户修改一个区间的值时,如果连同其子孙全部修改,则改动的节点数必定会远远超过O(log n)个。因而,如果要想把区间修改操作也控制在O(log n)的时间内,只修改O(log n)个节点的信息就成为必要。
以相同的方式更新某区间时,并不去真正更新其子区间,而是以某种方式把这个操作记录下来,等下一次访问到该区间并需要访问其子区间时,在访问的同时把子区间的值进行更改!这就称为懒操作。代码如下:
void push_down(int id,int sign){//sign=1表示入住,sign=0表示退房
tree[id].occ=-1;//更新自己和孩子的懒操作标记
tree[id<<1].occ=tree[id<<1|1].occ=sign;
if(sign==1){ //更新子节点
tree[id<<1].cl=tree[id<<1|1].cl=tree[id<<1].cr=tree[id<<1|1].cr=0;
tree[id<<1].max=tree[id<<1|1].max=0;
}else{
int len=tree[id<<1].rr-tree[id<<1].ll+1;
tree[id<<1].cl=tree[id<<1].cr=len;
tree[id<<1].max=len;
len=tree[id<<1|1].cr=tree[id<<1|1].rr-tree[id<<1|1].ll+1;
tree[id<<1|1].cl=len;
tree[id<<1|1].max=len;
}
}
具体解答请看下面AC过的代码:
import java.io.StreamTokenizer;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.PrintWriter;
import java.io.OutputStreamWriter;
import java.io.IOException;
class Tree{
int ll,rr,mid;
/* max表示结点管理的区间最大的连续子区间有多大,cl表示区间的最左边有多少连续的区间,
cr表示区间的右边有多少连续的子区间 */
int max,cl,cr;
int occ;//occ==0表示空,occ=1表示全部入住,occ=-1表示有空有住
}
public class Main{
Tree tree[];
public Main(){
tree=new Tree[32766];
for(int i=0;i<tree.length;i++){
tree[i]=new Tree();
}
}
void build(int id,int ll,int rr){
tree[id].ll=ll;tree[id].rr=rr;tree[id].mid=(ll+rr)>>1;
//刚开始建树,都是空的,所以可以这样写
tree[id].max=tree[id].cl=tree[id].cr=rr-ll+1;
tree[id].occ=0;
if(ll==rr)return;
build(id<<1,ll,tree[id].mid);
build(id<<1|1,tree[id].mid+1,rr);
}
//懒操作
void push_down(int id,int sign){//sign=1表示入住,sign=0表示退房
tree[id].occ=-1;//更新自己和孩子的懒操作标记
tree[id<<1].occ=tree[id<<1|1].occ=sign;//表示全空或者全住
if(sign==1){
tree[id<<1].cl=tree[id<<1|1].cl=tree[id<<1].cr=tree[id<<1|1].cr=0;
tree[id<<1].max=tree[id<<1|1].max=0;
}else{
int len=tree[id<<1].rr-tree[id<<1].ll+1;
tree[id<<1].cl=tree[id<<1].cr=len;
tree[id<<1].max=len;
len=tree[id<<1|1].cr=tree[id<<1|1].rr-tree[id<<1|1].ll+1;
tree[id<<1|1].cl=len;
tree[id<<1|1].max=len;
}
}
//更新区间
void update(int id ,int ll,int rr,int sign){//sign=1入住,sign=0表示退房
if(tree[id].ll==ll&&tree[id].rr==rr){//找到区间
tree[id].occ=sign;
int len=tree[id].rr-tree[id].ll+1;
if(sign==1) len=0;
tree[id].cl=tree[id].cr=len;
tree[id].max=len;
return;
}
if(tree[id].occ==1)
push_down(id,1);//执行到这行代码意味着 tree[id]的子区间要更改了,所以需要执行一次push_down
if(tree[id].occ==0)
push_down(id,0);
if(rr<=tree[id].mid){
update(id*2,ll,rr,sign);
}else if(ll>tree[id].mid){
update(id*2+1,ll,rr,sign);
}else{
update(id*2,ll,tree[id].mid,sign);
update(id*2+1,tree[id].mid+1,rr,sign);
}
//子区间更新了,必须更新父区间
//需要修改的就只有3个值:max,cl,cr 分别代表最长连续个数为多少,最左边有多少个空闲,最右边有多少个空闲
if(tree[id].occ==-1){//表示有空有住
if(tree[id<<1].occ==0){
tree[id].cl=tree[id*2].cl+tree[id<<1|1].cl;
}else{
tree[id].cl=tree[id<<1].cl;
}
if(tree[id<<1|1].occ==0){
tree[id].cr=tree[id*2].cr+tree[id<<1|1].cr;
}else{
tree[id].cr=tree[id<<1|1].cr;
}
//求tree[id].max
int len=tree[id<<1].cr+tree[id<<1|1].cl;
tree[id].max=Math.max(len,Math.max(tree[id<<1].max,tree[id<<1|1].max));
}else{//表示全空或者全住
int len;
if(sign==1)
len=0;
else
len=tree[id].rr-tree[id].ll+1;
tree[id].max=tree[id].cl=tree[id].cr=len;
}
if(tree[id*2].occ==tree[id*2+1].occ)
tree[id].occ=tree[id*2].occ;
}
int getMax(){
return tree[1].max;
}
public static void main(String[] args) throws IOException{
//注:用Scanner in=new Scanner(System.in)超时!!!!!!!!
StreamTokenizer st = new StreamTokenizer(new BufferedReader(
new InputStreamReader(System.in)));
PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
st.nextToken();
int n= (int) st.nval;
st.nextToken();
int p=(int) st.nval;
Main ma=new Main();
int sign;
int ll,rr;
ma.build(1,1,n);
for(int i=0;i<p;i++){
st.nextToken();
sign=(int) st.nval;
if(sign==3){
out.printf("%d\n",ma.getMax());
}else{
st.nextToken();
ll=(int) st.nval;
st.nextToken();
rr=(int) st.nval;
rr=ll+rr-1;
if(sign==2)
sign=0;
ma.update(1,ll,rr,sign);
}
}
out.flush();
}
}
以上代码参考了:http://sbp810050504.blog.51cto.com/2799422/1023633
源码下载: