求二叉树上任意两个节点的最近公共父节点

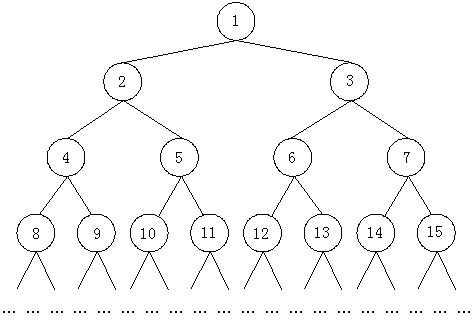
北大百练题2756:
    如上图所示，由正整数1, 2, 3, ...组成了一棵无限大的二叉树。从某一个结点到根结点（编号是1的结点）都有一条唯一的路径，比如从10到根结点的路径是(10, 5, 2, 1)，从4到根结点的路径是(4, 2, 1)，从根结点1到根结点的路径上只包含一个结点1，因此路径就是(1)。对于两个结点x和y，假设他们到根结点的路径分别是(x1, x2, ... ,1)和(y1, y2, ... ,1)（这里显然有x = x1，y = y1），那么必然存在两个正整数i和j，使得从xi 和 yj开始，有xi = yj , xi + 1 = yj + 1, xi + 2 = yj + 2,... 现在的问题就是，给定x和y，要求xi（也就是yj）。

输入
输入只有一行，包括两个正整数x和y，这两个正整数都不大于1000。

输出
输出只有一个正整数xi。

样例输入
10 4

样例输出
2

    这个题目要求树上任意两个节点的最近公共父节点。分析这棵树的结构不难看出，
不论奇数偶数，每个数对 2 做整数除法，就走到它的上层结点。我们可以每次让较大的一个数（也就是在树上位于较低层次的节点）向上走一个结点，直到两个结点相遇。如果两个节点位于同一层，并且它们不相等，可以让其中任何一个先往上走，然后另一个再往上走，直到它们相遇。设 father(x, y)表示整数 x 和 y的最近公共子节点，那么，根据比较 x 和 y 的值，我们得到三种情况：
1) x 与 y 相等，则 father(x, y)等于 x 并且等于 y；
2）x 大于 y，则 father(x, y)等于 father(x/2, y)；
3）x 大于 y，则 father(x, y)等于 father(x y/2)；

AC代码：

import java.util.Scanner;
  public class Main{
 
   static int father(int x,int y){
    if(x==y)
       return x;
    else if(x>y)
      return father(x/2,y);
    else
      return father(x,y/2);

   }
 
  public static void main(String args[]){
     Scanner in=new Scanner(System.in);    
    int x=in.nextInt();
    int y=in.nextInt();
    System.out. println(father(x,y));
  }
 }