直接插入排序
直接插入排序的原理:先将原序列分为有序区和无序区,然后再经过比较和后移操作将无序区元素插入到有序区中,
下面表格中,排序之前取第一个元素为有序区10,无序区9到4,带颜色为有序区。
| 待排序数组 | 10 | 9 | 8 | 7 | 6 | 5 | 4 |
| 第一次排序 | 9 | 10 | 8 | 7 | 6 | 5 | 4 |
| 第二次排序 | 8 | 9 | 10 | 7 | 6 | 5 | 4 |
| 第三次排序:详细步骤 | |||||||
| 1:将7拿出来 | 7 | ||||||
| 2:7跟10比较后 | 8 | 9 | 10 | 6 | 5 | 4 | |
| 3:7跟9比较后 | 8 | 9 | 10 | 6 | 5 | 4 | |
| 4:7跟8比较后 | 8 | 9 | 10 | 6 | 5 | 4 | |
| 5:将7插入 | 7 | 8 | 9 | 10 | 6 | 5 | 4 |
找到了一个比较直观的图片
/**
* 直接插入排序
*
* @param ts
*/
public static <T extends Comparable<? super T>> void insertionSort(T[] ts) {
int x;
// 有序区:ts[0]
// 无序区:ts[1]到ts[ts.length-1]
for (int i = 1; i < ts.length; i++) {
T tem = ts[i];
// 从数组的ts[i]元素开始,向前(有序区)比较
for (x = i; x > 0 && tem.compareTo(ts[x - 1]) < 0; x--)
ts[x] = ts[x - 1]; // 如果已排序的元素大于新元素,将该元素移到下一位置
ts[x] = tem; // 将 ts[i] 放到正确位置上
}
}
1.时间复杂度:O(n^2)
直接插入排序耗时的操作有:比较+后移赋值。时间复杂度如下:
1) 最好情况:序列是升序排列,在这种情况下,需要进行的比较操作需(n-1)次。后移赋
值操作为0次。即O(n)
2) 最坏情况:序列是降序排列,那么此时需要进行的比较共有n(n-1)/2次。后移赋值操作是
比较操作的次数加上 (n-1)次。即O(n^2)
3) 渐进时间复杂度(平均时间复杂度):O(n^2)
2.空间复杂度:O(1)
从实现原理可知,直接插入排序是在原输入数组上进行后移赋值操作的(称“就地排序”),所需开辟的辅助空间跟输入数组规模无关,所以空间复杂度为:O(1)
3.稳定性
直接插入排序是稳定的,不会改变相同元素的相对顺序。
4.优化改进
1) 二分查找插入排序:因为在一个有序区中查找一个插入位置,所以可使用二分查找,减
少元素比较次数提高效率。
2) 希尔排序:如果序列本来就是升序或部分元素升序,那么比较+后移赋值操作次数就会
减少。希尔排序正是通过分组的办法让部分元素升序再进行整个序列排序。(原因是,
当增量值很大时数据项每一趟排序需要的个数很少,但数据项的距离很长。当增量值减小
时每一趟需要和动的数据增多,此时已经接近于它们排序后的最终位置。)
二分查找插入排序
二分查找插入排序的原理:是直接插入排序的一个变种,区别是:在有序区中查找新元
素插入位置时,为了减少元素比较次数提高效率,采用二分查找算法进行插入位置的确定。
注意下面,在用二分法查到插入位置时,移动已排序元素时,用java的本地方法copy数组,比用for循快很多。当然当数据量过10w跟希尔排序还不是一个级别
/**
* 二分查找插入排序
* 移位用一般for循环:13-14行
* 移位用java类库中本地方法 16行
* @param ts
*/
public static <T extends Comparable<? super T>> void insertionBinarySort(T[] ts) {
// 有序区:ts[0]
// 无序区:ts[1]到ts[ts.length-1]
for (int i = 1; i < ts.length; i++) {
T tem = ts[i]; // 待插入元素
int index = getStartByBinary(ts, i - 1, tem); // 插入位置
// for (int x = i; x > index; x--)// 插入位置 到 已排序边界 统一后移一位
// ts[x] = ts[x - 1];
// 将index后面i-index个元素(包含index) 移到 index+1后面(包含index+1)
System.arraycopy(ts, index, ts, index + 1, i - index);
ts[index] = tem; // 将待插入元素放到index位置上
}
}
/**
* 查找待排序元素该插入位置
* @param ts数组
* @param i 已排序边界(不包括待排元素位置)
* @param t 待排元素
* @return 应该插入位置
*/
private static <T extends Comparable<? super T>> int getStartByBinary(T[] ts, int i, T t) {
int index = 0, end = i;//每次查找的范围 index上界,end下界
while (index <= end) {
int binary = (index + end) / 2;
if (t.compareTo(ts[binary]) < 0)
end = binary - 1;
else
index = binary + 1;// 可插入位置 0~i+1
}
return index;
}
1. 时间复杂度 :
for循环: O(n^2)
java本地方法copy:不确定
二分查找插入位置,因为不是查找相等值,而是基于比较查插入合适的位置,所以必须
查到最后一个元素才知道插入位置。
二分查找最坏时间复杂度:当2^X>=n时,查询结束,所以查询的次数就为x,而x等于log2n(以2为底,n的对数)。即O(log2n)
所以,二分查找排序比较次数为:x=log2n
二找插入排序耗时的操作有:比较 + 后移赋值。时间复杂度如下:
1) 最好情况:查找的位置是有序区的最后一位后面一位,则无须进行后移赋值操作,其比较
次 数为:log2n 。即O(log2n)
2) 最坏情况:查找的位置是有序区的第一个位置,则需要的比较次数为:log2n,需要的赋
值操作次数
for循环: n(n-1)/2加上 (n-1) 次。即O(n^2)
java本地方法copy:不确定
3) 渐进时间复杂度(平均时间复杂度)
for循环:O(n^2)
java本地方法copy:不确定
2. 空间复杂度:O(1)
从实现原理可知,二分查找插入排序是在原输入数组上进行后移赋值操作的(称“就地
排序”),所需开辟的辅助空间跟输入数组规模无关,所以空间复杂度:O(1)
3. 稳定性
二分查找排序是稳定的,不会改变相同元素的相对顺序。
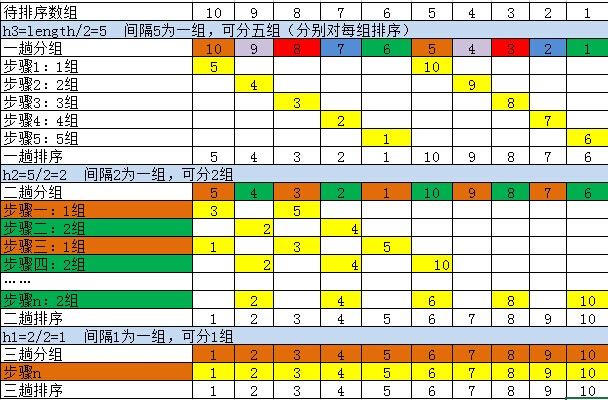
希尔缩小增量排序(可能有更好的增量)
希尔排序名称来源于它的发明者Donald Shell , 该算法是冲破二次时间屏障的第一批算法之一。不过直到它最初被发现的若干年后才证明了它的亚二次时间界。
希尔排序使用一个序列h1<h2<h3.....ht,叫做增量序列。只要h1=1,任何增量序列都是可行的。不过有些增量序列比另外一些增量序列更好(这里不讨论)。