JAVA总结——静态科赫曲线和科赫雪花
经过几天的分析和计算,终于画出了传说中的科赫曲线(当然只是最初步的静态的曲线)。在这个过程中学到了一些新的东西,总体来说还是挺好玩的。
depth=1

depth=3

depth=7
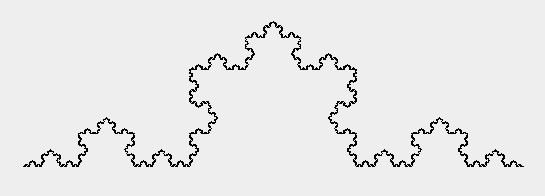
代码如下:创建了2个类
第一个类:DrawBoard
第二个类:BoardListener
总体来说,遇到的困难有以下几个:
1.存点问题:
(x5,y5)的情况要计算3种,每种的(x3,y3)(x4,y4)算法相同,只有(x5,y5)算法
不同,要用选择来讨论情况。
2.x3,y3,x4,y4一定要定义成局部变量,即double x3=(2*x1+x2)/3;而不能在开头定义double x3, x3=(2*x1+x2)/3!!!!!!
3.递归函数中应该写成depth-1,而不能是depth--!
将一个正三角形的每条边都做如上变换,即可得到科赫雪花
[img]

[/img]
代码如下
depth=1

depth=3

depth=7

代码如下:创建了2个类
第一个类:DrawBoard
package source;
import java.awt.Graphics;
import javax.swing.JFrame;
public class DrawBoard extends JFrame{
Graphics g;
//主函数
public static void main(String [] args){
DrawBoard db = new DrawBoard();
db.createboard();
}
//创建窗体
public void createboard(){
this.setTitle("科赫曲线");
this.setSize(800, 800);
this.setDefaultCloseOperation(3);
this.setResizable(false);
this.setVisible(true);
//创建一个画布对象
Graphics g =this.getGraphics();
BoardListener lis = new BoardListener(g);
this.addMouseListener(lis);
}
}
第二个类:BoardListener
package source;
import java.awt.Graphics;
import java.awt.event.MouseEvent;
import java.awt.event.MouseListener;
public class BoardListener implements MouseListener{
Graphics g;
// double x1,x2,x3,x4,x5,y1,y2,y3,y4,y5,k;
int depth = 7;
public BoardListener(Graphics g1){
g=g1;
}
public void mouseClicked(MouseEvent e) {
digui(100,400,600,400,this.depth);
}
public void mouseEntered(MouseEvent arg0) {
}
public void mouseExited(MouseEvent arg0) {
}
public void mousePressed(MouseEvent arg0) {
}
public void mouseReleased(MouseEvent arg0) {
}
public void digui(double x1,double y1,double x2,double y2,int depth){
if(depth<=1){
g.drawLine((int)x1,(int)y1,(int)x2,(int)y2);
}
else {
double x3=(2*x1+x2)/3;double y3=(2*y1+y2)/3;
double x4=(x1+2*x2)/3;double y4=(y1+2*y2)/3;
double x5=0,y5=0;
double k=(y4-y3)/(x4-x3);
if(y3==y4){
x5=(x3+x4)/2;y5=y3-(x4-x3)*Math.sqrt(3)/2;
}
else{
if(k<0){
x5=x1;y5=y4;
}
if(k>0){
x5=x2;y5=y3;
}
}
digui(x1,y1,x3,y3,depth-1);
digui(x3,y3,x5,y5,depth-1);
digui(x5,y5,x4,y4,depth-1);
digui(x4,y4,x2,y2,depth-1);
}
}
}
总体来说,遇到的困难有以下几个:
1.存点问题:
(x5,y5)的情况要计算3种,每种的(x3,y3)(x4,y4)算法相同,只有(x5,y5)算法
不同,要用选择来讨论情况。
2.x3,y3,x4,y4一定要定义成局部变量,即double x3=(2*x1+x2)/3;而不能在开头定义double x3, x3=(2*x1+x2)/3!!!!!!
3.递归函数中应该写成depth-1,而不能是depth--!
将一个正三角形的每条边都做如上变换,即可得到科赫雪花
[img]

[/img]
代码如下
package source;
import java.awt.Graphics;
import java.awt.event.MouseEvent;
import java.awt.event.MouseListener;
public class BoardListener implements MouseListener{
Graphics g;
int depth = 10;
public BoardListener(Graphics g1){
g=g1;
}
public void mouseClicked(MouseEvent e) {
digui1(100,200,600,200,this.depth);
digui2(100,200,350,633,this.depth);
digui3(600,200,350,633,this.depth);
}
public void mouseEntered(MouseEvent arg0) {
}
public void mouseExited(MouseEvent arg0) {
}
public void mousePressed(MouseEvent arg0) {
}
public void mouseReleased(MouseEvent arg0) {
}
//第一个递归函数
public void digui1(double x1,double y1,double x2,double y2,int depth){
if(depth<=1){
g.drawLine((int)x1,(int)y1,(int)x2,(int)y2);
}
else {
//一定要把x1...x5定义成局部变量!!!
double x3=(2*x1+x2)/3;double y3=(2*y1+y2)/3;
double x4=(x1+2*x2)/3;double y4=(y1+2*y2)/3;
double x5=0,y5=0;
double k=(y4-y3)/(x4-x3);
if(y3==y4){
x5=(x3+x4)/2;y5=y3-(x4-x3)*Math.sqrt(3)/2;
}
else{
if(k<0){
x5=x1;y5=y4;
}
if(k>0){
x5=x2;y5=y3;
}
}
digui1(x1,y1,x3,y3,depth-1);
digui1(x3,y3,x5,y5,depth-1);
digui1(x5,y5,x4,y4,depth-1);
digui1(x4,y4,x2,y2,depth-1);
}
}
//第二个递归函数
public void digui2(double x1,double y1,double x2,double y2,int depth){
if(depth<=1){
g.drawLine((int)x1,(int)y1,(int)x2,(int)y2);
}
else {
//一定要把x1...x5定义成局部变量!!!
double x3=(2*x1+x2)/3;double y3=(2*y1+y2)/3;
double x4=(x1+2*x2)/3;double y4=(y1+2*y2)/3;
double x5=0,y5=0;
double k=(y4-y3)/(x4-x3);
if(y3==y4){
x5=(x3+x4)/2;y5=y3+(x4-x3)*Math.sqrt(3)/2;
}
else{
if(k<0){
x5=x2;y5=y3;
}
if(k>0){
x5=x1;y5=y4;
}
}
digui2(x1,y1,x3,y3,depth-1);
digui2(x3,y3,x5,y5,depth-1);
digui2(x5,y5,x4,y4,depth-1);
digui2(x4,y4,x2,y2,depth-1);
}
}
public void digui3(double x1,double y1,double x2,double y2,int depth){
if(depth<=1){
g.drawLine((int)x1,(int)y1,(int)x2,(int)y2);
}
else {
//一定要把x1...x5定义成局部变量!!!
double x3=(2*x1+x2)/3;double y3=(2*y1+y2)/3;
double x4=(x1+2*x2)/3;double y4=(y1+2*y2)/3;
double x5=0,y5=0;
double k=(y4-y3)/(x4-x3);
if(y3==y4){
x5=(x3+x4)/2;y5=y3+(x3-x4)*Math.sqrt(3)/2;
}
else{
if(k<0){
x5=x1;y5=y4;
}
if(k>0){
x5=x2;y5=y3;
}
}
digui3(x1,y1,x3,y3,depth-1);
digui3(x3,y3,x5,y5,depth-1);
digui3(x5,y5,x4,y4,depth-1);
digui3(x4,y4,x2,y2,depth-1);
}
}
}