8个皇后问题 java递归可以算出
背景:"八皇后问题是一个古老而著名的问题,是回溯算法的典型例题。该问题是十九世纪著名的数学家高斯1850年提出:在8X8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解,后来有人用图论的方法解出92种结果。"——百度百科
--40357162 (需要先理解这个数列 8个数列,列值0-7;每个结果都由0,1,2,3,4,5,6,7组成.)
通过分析问题,不难发现一个序列只要符合两点要求,就可实现8颗皇后的同盘并存:
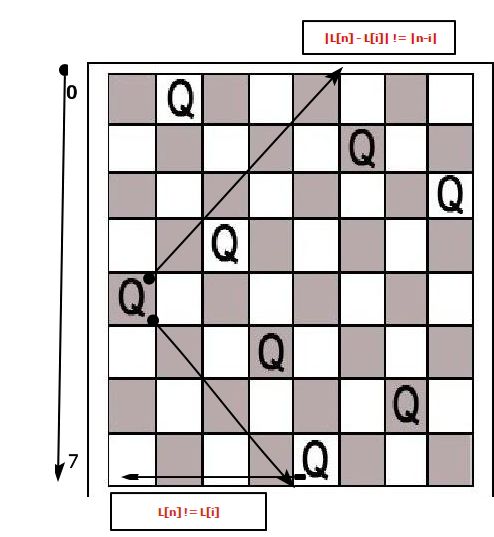
1)序列L中第n元素L[n]的本身值不能和其前任意元素L[i]的本身值相等,即:L[n] != L[i | (0, n-1)];
2)序列L中任意元素L[n]的本身值与其前任意元素L[i]的本身值之差的绝对值,不能和L[n]的位置值n与L[i]的位置值i之差的绝对值相等,即:| L[n] - L[i] | != |n - i|, 0 <= i <= n-1;
图
再加上边界限制条件,我们就可以利用以上两条原则来构造递归结构。
其实不仅仅是八皇后问题,10皇后,18皇后,甚至100皇后都符合这两条规则,所以我们可以把问题引申为求解 “N Queens Puzzle”。
实例代码(全):
import java.util.ArrayList;
public class test1 {
private static ArrayList<Integer> al = new ArrayList<Integer>();
private static ArrayList<ArrayList> record = new ArrayList<ArrayList>();
private static int MAX = 0;
private static int amount = 1;
public static void main(String[] args) {
//MAX = Integer.parseInt(args[0]);
MAX = 8;
while(al.size()==0 || al.get(0)!=8){
work();
System.out.print("\n" + amount + ") ");
record.add((ArrayList)al.clone());
output(record.get(record.size()-1));
al.remove(al.size()-1);
endAddOne();
amount++;
}
}
private static void work(){
int i = 0;
while(al.size() < MAX){
if( isOK(al, i)){
al.add(i);
i = 0;
}
else{
if( i < MAX-1 ){
i++;
}
else{
endAddOne();
i = 0;
}
}
}
}
//only check the last one of the arraylist;
//could not be like: either | al[i] - a | == | i - a | or al[i] == a;
//if not satisfied, returns a false;
//else returns a true;
private static boolean isOK(ArrayList<Integer> al, int a){
int size = al.size();
if(size < 1) return true;
if(size <= MAX){
for(int i=0; i<size; i++){
if(a == al.get(i) || Math.abs((a - al.get(i))/(float)(size - i)) == 1){
return false;
}
}
return true;
}
return false;
}
private static void endAddOne(){
if(al.size()==0){
System.exit(1);
}
int last = al.get(al.size()-1) + 1;
if(last >= MAX){
al.remove(al.size()-1);
endAddOne();
}
else{
al.remove(al.size()-1);
if(isOK(al, last)){
al.add(last);
}
else{
al.add( last);
endAddOne();
}
}
}
private static void output(ArrayList<Integer> al){
for(int i=0; i<al.size(); i++){
System.out.print(al.get(i) + " ");
}
}
}
输出结果:
1) 0 4 7 5 2 6 1 3 2) 0 5 7 2 6 3 1 4 3) 0 6 3 5 7 1 4 2 4) 0 6 4 7 1 3 5 2 5) 1 3 5 7 2 0 6 4 6) 1 4 6 0 2 7 5 3 7) 1 4 6 3 0 7 5 2 8) 1 5 0 6 3 7 2 4 9) 1 5 7 2 0 3 6 4 10) 1 6 2 5 7 4 0 3 11) 1 6 4 7 0 3 5 2 12) 1 7 5 0 2 4 6 3 13) 2 0 6 4 7 1 3 5 14) 2 4 1 7 0 6 3 5 15) 2 4 1 7 5 3 6 0 16) 2 4 6 0 3 1 7 5 17) 2 4 7 3 0 6 1 5 18) 2 5 1 4 7 0 6 3 19) 2 5 1 6 0 3 7 4 20) 2 5 1 6 4 0 7 3 21) 2 5 3 0 7 4 6 1 22) 2 5 3 1 7 4 6 0 23) 2 5 7 0 3 6 4 1 24) 2 5 7 0 4 6 1 3 25) 2 5 7 1 3 0 6 4 26) 2 6 1 7 4 0 3 5 27) 2 6 1 7 5 3 0 4 28) 2 7 3 6 0 5 1 4 29) 3 0 4 7 1 6 2 5 30) 3 0 4 7 5 2 6 1 31) 3 1 4 7 5 0 2 6 32) 3 1 6 2 5 7 0 4 33) 3 1 6 2 5 7 4 0 34) 3 1 6 4 0 7 5 2 35) 3 1 7 4 6 0 2 5 36) 3 1 7 5 0 2 4 6 37) 3 5 0 4 1 7 2 6 38) 3 5 7 1 6 0 2 4 39) 3 5 7 2 0 6 4 1 40) 3 6 0 7 4 1 5 2 41) 3 6 2 7 1 4 0 5 42) 3 6 4 1 5 0 2 7 43) 3 6 4 2 0 5 7 1 44) 3 7 0 2 5 1 6 4 45) 3 7 0 4 6 1 5 2 46) 3 7 4 2 0 6 1 5 47) 4 0 3 5 7 1 6 2 48) 4 0 7 3 1 6 2 5 49) 4 0 7 5 2 6 1 3 50) 4 1 3 5 7 2 0 6 51) 4 1 3 6 2 7 5 0 52) 4 1 5 0 6 3 7 2 53) 4 1 7 0 3 6 2 5 54) 4 2 0 5 7 1 3 6 55) 4 2 0 6 1 7 5 3 56) 4 2 7 3 6 0 5 1 57) 4 6 0 2 7 5 3 1 58) 4 6 0 3 1 7 5 2 59) 4 6 1 3 7 0 2 5 60) 4 6 1 5 2 0 3 7 61) 4 6 1 5 2 0 7 3 62) 4 6 3 0 2 7 5 1 63) 4 7 3 0 2 5 1 6 64) 4 7 3 0 6 1 5 2 65) 5 0 4 1 7 2 6 3 66) 5 1 6 0 2 4 7 3 67) 5 1 6 0 3 7 4 2 68) 5 2 0 6 4 7 1 3 69) 5 2 0 7 3 1 6 4 70) 5 2 0 7 4 1 3 6 71) 5 2 4 6 0 3 1 7 72) 5 2 4 7 0 3 1 6 73) 5 2 6 1 3 7 0 4 74) 5 2 6 1 7 4 0 3 75) 5 2 6 3 0 7 1 4 76) 5 3 0 4 7 1 6 2 77) 5 3 1 7 4 6 0 2 78) 5 3 6 0 2 4 1 7 79) 5 3 6 0 7 1 4 2 80) 5 7 1 3 0 6 4 2 81) 6 0 2 7 5 3 1 4 82) 6 1 3 0 7 4 2 5 83) 6 1 5 2 0 3 7 4 84) 6 2 0 5 7 4 1 3 85) 6 2 7 1 4 0 5 3 86) 6 3 1 4 7 0 2 5 87) 6 3 1 7 5 0 2 4 88) 6 4 2 0 5 7 1 3 89) 7 1 3 0 6 4 2 5 90) 7 1 4 2 0 6 3 5 91) 7 2 0 5 1 4 6 3 92) 7 3 0 2 5 1 6 4
此文参考自:http://xman--bsn.blog.sohu.com/38195158.html