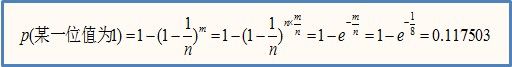海量数据处理利器之Hash——在线邮件地址过滤 - MyDetail

原帖地址：http://www.cnblogs.com/fengfenggirl/p/bloom_filter.html

　　标题用了了海量数据（Massive datasets）而不用大数据（Big data）。感觉大数据还是略微有点虚，来点实际的。

一、需求

　　现在我们需要设计一个在线过滤垃圾邮件地址的方案，我们的数据库里面已经有10亿个合法的邮件地址（称为合法地址集S），当有新的邮件发过来时，要检查这个邮件地址是不是在我们的数据库里面，如果在，我们接收邮件，如果不在，我们就把它当做垃圾邮件过滤掉。

二、直觉想到的方法

　　一拿到这个问题，我就想到了用log(n)的折半查找，先将10亿个邮件地址排序，当收到一个邮件地址时，我利用折半查找，看邮件地址是否在S中，log(1,000,000,000) = 29.89约等于30，对每一个邮件地址我最多也只需要查找30次，感觉也挺快的，应该能满足要求。仔细想一下，折半查找必须放入内存，10个邮件地址还差不多，10亿个邮件地址我们来算一算有多大，邮件地址平均长度按20个字符计算，一个字符占用2Byte，一个email就占了40B，1,000,000,000X40B = 40GB，内存顶得住么，当然可以分多段进行折半，当分段需要多次I/O操作，需要的时间已经不是在线过滤所能承受的了。

三、利用hash处理问题

　　当数据量很大时，我们一些快速的方法已经不是多给点时间就能解决的，是压根解决不了，折半查找的方法在可接受的范围内是不可行的。我们来介绍一种神奇的方法，利用hash和位图实现常量时间确定邮件地址是否在S中。

1、过滤器初步设计

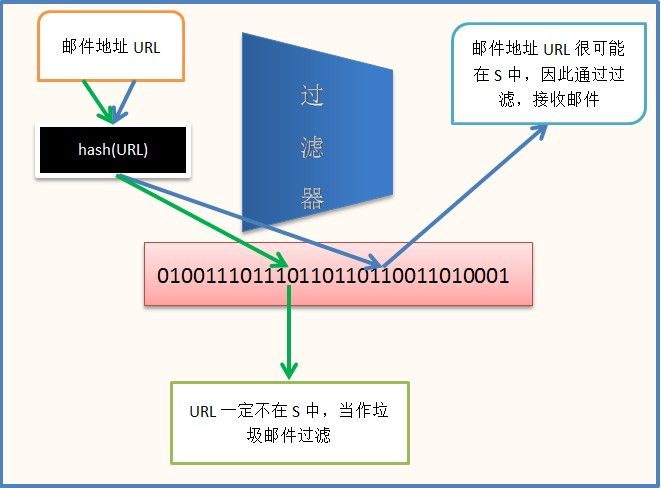
　　我们申请一个1GB的内存（虽然大了点，但现在的PC都顶得住了），1B共8位，1GB共有80亿位（实际应该为8X2^30=8,589,934,592位，但为了方便叙述，我们这里用80亿位）这个位图用B表示，B[i]表示位图的第i位；设计一个hash函数，将邮件地址映射到1-80亿的整数空间上。先将80亿位全部置为0，然后对S中的每一个邮件地址进行hash，hash得到一个整数k，就将第k位 置为1，即B[k]=1，如果hash函数设计得好，hash完S后，80亿的位图应该有10亿个(实际值比10亿小，后面会详细分析)位的值为1，当收到邮件时，对邮件地址进行hash，记hash得到的结果为p，如果B[p]=0，则邮件地址一定不再S中，即当作垃圾邮件过滤；如果B[p]=1，则邮件通过过滤，接收邮件。可以结合下图理解：　　

　　注意当B[p]=1时，我们并不是说新邮件地址一定在S中，而是说很可能在S中。B[p]=1只能说明S中一定有一个邮件地址URL，使得hash(URL)=p，而这不能保证其他垃圾邮件地址的hash值不等于p。B[p]=0说明S中不存在邮件地址URL，使得hash(URL)=p，从而新邮件地址一定不在S中。因此，被当作垃圾邮件过滤的邮件一定不包含合法的地址，而通过过滤的地址仍然有可能是垃圾邮件地址，大约有1/8（1/8=10亿/80亿，不过实际值比1/8小，后面会详细分析）的垃圾邮件通过过滤，1/8也称为伪阳率。

　　这样的方案直接上线还是有问题的，因为伪阳率比较高，我们来计算一下照这种方案我们接收的邮件中垃圾邮件的比率是多少。根据新闻报道全球80%的邮件是垃圾邮件，于是P(接收到的垃圾邮件/接收的邮件)=(1/8*80%)/(20%+1/8*80%)=1/3(33.33%)，也就是说平均收三封邮件就有一封是垃圾邮件，这对用户来说是不能忍受的，方案必须优化，不过我们应该看到，我们在不漏掉任何一个合法邮件的前提下过滤了7/8的垃圾邮件，已经初显hash利器之锋芒了。

2、伪阳率分析

　　前面我们提到过伪阳率并不是1/8，它比1/8略小，现在我们从概率的角度来计算一下伪阳率的真实值。

　　先来看另外一个简单的例子，假设我们有m个飞镖、n个靶，一个射击高手（所谓高手就是无论怎么射击都不会脱靶的神人）把这m个飞镖一个接一个的射向这n个靶，假设一个飞镖击中每个耙的概率相等，问高手射击完之后，某一个靶上面一个飞镖也没有的概率是多少？这个计算并不难，对于任意的一个耙W，被某一个飞镖击中的概率P(耙W被某飞镖击中)=1/n，那么不被某一飞镖击中的概率P(耙W不被某飞镖击中)=1-1/n，射击m个飞镖可以看做是m次独立重复事件，于是P(耙W不被任何一个飞镖击中) = (1-1/n)^m，这也就是某一个耙上面一个飞镖也没有的概率。现在我们再问，某一个飞镖至少有一个飞镖的概率？有了上一步的分析，可以知道p(耙W上至少有一个飞镖)=1-P(耙W不被任何一个飞镖击中)=1- (1-1/n)^m。

　　现在回到我们之前的问题，我们的80亿个位相当于上例中的n个耙，10亿个合法邮件地址相当于m个飞镖，hash函数相当于射击高手，集合S经过hash后，某一位值为1（即至少被击中一次）的概率P=1-((1-1/8,000,000,000)^1,000,000,000)，直接用计算器计算这个值是不现实的，因为1除以80亿已经下溢出为0，再进行10亿次累乘已经没有意义。这个值的计算需要用到极限的知识，伟大的数学家已经帮我们算好了，我们只需要套一下公式，还记得下面这个公式吗：

　　可以看到0.1175与我们初步估计的1/8=0.125相差并不大，所以我们之前用1/8分析是合理的。

　　p(某一位值为1)也就是伪阳率，即垃圾邮件被接收的概率，这里再解释一下为什么p(某一位值为1)就是垃圾邮件被接收的概率：我们收到一个新邮件，将地址hash为p，B[p]为1的概率即为我们接受邮件的概率，显然P(B[p]=1)=p(某一位值为1)。

3、优化过滤器，降低伪阳率

　　前面我们计算过了，按上面的方案，用户平均每接受3封邮件就有1封是垃圾邮件。我们对过滤器进行改进，设置k个hash函数h1,h2,...,hk，每一个hash函数的映射空间都是1-80亿的整数集。对S中的每一个邮件地址都在k个hash函数进行计算，记hash的结果为p1,p2,...,pk，则将对于位 置1，即B[pi]=1（i=1,2,..,k）， 当新邮件发来时，我们对新邮件地址也在k个hash函数上计算，同样记hash的结果为p1,p2,...,pk，如果hash结果的所有位都为1，则接受邮件，否则新地址一定不再S中，当作垃圾邮件过滤。当k=2时的示意图如下：　　

　　跟1个hash函数一样，设置k个hash函数也不会漏掉任何一个合法邮件，而接受的邮件里仍然还是会有垃圾邮件，现在我们来计算此时的伪阳率,根据前面的分析，对单个hash函数的情况下，一个位为1的概率为P=1-e^(-m/n)。

　　现在有k个hash函数，相当于我们现在有k*m个飞镖，于是此时某一位为1的概率为P=1-e^(-k*m/n)，但此时伪阳率不再等于p(某一位值为1)，只有在k个hash结果所在位都为1的情况下我们才接收邮件，而P(k个hash结果所在位都为1)=(1-e^(-k*m/n))^k，因此伪阳率为(1-e^(-k*m/n))^k，当k=2时，伪阳率P=(1-e^(-1/4))^2=0.048929094，这个值比一个hash函数下的0.1175小了很多，那是不是伪阳率也越低呢，我们来看一下曲线图：　　

　　发现伪阳率随着k的增大先减小后增大，最后趋于1，最优的k值在5,6之间，但k取整数，因此k=6时伪阳率最小，即设置6个hash函数，可以得到最小的伪阳率，此时伪阳率的值为0.0216。一般情况下，最优值k=ln(2)*n/m，记住这个答案就可以了，如果感兴趣，可以参看下面的计算过程：

　　现在我们再来计算一下最优情况下k=6时，接收到的垃圾邮件在接收的邮件中的比例 P(接收到的垃圾邮件/接收的邮件)=80%*0.0216/(20%+80%*0.0216)=0.077490775=1/13，即平均每接收13封邮件有一封是垃圾邮件，我感觉这跟我的邮箱情况差不多，达到了用户可以承受的范围。

　　如果我们申请2G的内存，那么我们有160亿位，k=ln(2)*n/m=ln(2)*16=11.09，即k=10，此时伪阳率p=0.0004587， P(接收到的垃圾邮件/接收的邮件)=80%*0.0004587/(20%+80%*0.0004587)=0.00183144=1/546，也就是说平均接收546封邮件才收到一封垃圾邮件，这已经完全符合业务要求了，要知道这个方案处理速度很快，只需要计算几个hash函数，然后查位图，可在线计算（当然必须提前hash映射S）。

　　这个多个hash函数的顾虑器称为布隆过滤器（Bloom Filter）。

　　当有新的合法邮件添加时，将新合法邮件地址添加到S中，并进行k次hash，并将对应位置为1，这样新的合法邮件就不会被过滤，当新合法邮件添加到一定数量时，需要重新计算k，重新hash一遍S。

　　事实上，更多的垃圾邮件过滤是基于邮件内容的，可以在我们的过滤器过滤之后，进行自然语言处理内容分析过滤，我们的过滤器以及过滤了绝大部分垃圾邮件了。

　　我们见证了hash了处理海量数据的威力，这只是一个例子，相信大家可以在其他地方也能用的。

　　最后，我想说，终于发现以前的数学分析、高等代数、概率论有用了，不是吗？

参考资料：

　　[1].Anand Rajaraman, Jeffrey davaid UIIman. Mining of Massive Datasets. Cambridge University Presss 2012.

　　[2].维基百科.e (数学常数).https://zh.wikipedia.org/wiki/E_(%E6%95%B0%E5%AD%A6%E5%B8%B8%E6%95%B0). 2013.5.27

　　[3].Jure Leskovec.Stanford CS246 Mining Massive Data Sets.http://www.stanford.edu/class/cs246/.2013（很好的一门课，推荐）

　　[4].维基百科.Email spam.https://en.wikipedia.org/wiki/Email_spam.2013.6.21

　　ps:画图工具：word2010

　　　  数据处理：excel2010

　　　  感谢条子同学提供的数学证明指导！

　　感谢关注，欢迎评论。

本文链接：http://www.cnblogs.com/fengfenggirl/p/bloom_filter.html，转载请注明。