简单的图论算法
一、图的基本算法
1.广度优先搜索(BFS[breadth-first search]) //如果用邻接矩阵来遍历,需要O(v^2);如果用邻接表遍历,需要O(v+e)
2.深度优先搜索(DFS[depth-first search])//如果用邻接矩阵来遍历,需要O(v^2);如果用邻接表遍历,需要O(v+e)
3.拓扑排序(topological sorting) //O(v+e)
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若 ∈E(G),则u在线性序列中出现在v之前。
算法:
用以下的简单算法得到一个DAG的拓扑排序,而且,所有的拓扑排序都可以通过这个算法得到。
设需要进行拓扑排序的图为G,已经完成拓扑排序的顶点构成序列q。
| 一、开始时,置图G1=G,q为空序列; 二、如果图G1是空图,则拓扑排序完成,算法结束,得到的序列q就是图G的一个拓扑排序; 三、在图G1中找到一个没有入边(即入度为0)的顶点v,将v放到序列q的最后(这样的顶点v必定存在,否则图G1必定有圈;因为图G有圈,故不是DAG); 四、从图G1中删去顶点v以及所有与顶点v相连的边e(通过将与v邻接的所有顶点的入度减1来实现),得到新的图G1,转到第二步。 |
应用:
| 将DAG的每一个顶点对应一个事件,图中存在从A指向B的边表示事件A是事件B的一个前提条件。这样组成的图叫做AOV(Activity on Vertex)网。对AOV网进行拓扑排序,每一个排序结果表示一种可行的做事的先后顺序。 |
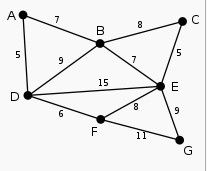
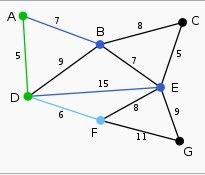
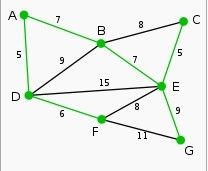
二、最小生成树(Minimum Spanning Tree)
Kruskal算法和Prim算法是寻找最小生成树的经典算法。首先先了解最小生成树的性质——
1、最小生成树的边数==顶点数-1,即e = v -1;
2、最小生成树无环状结构
3、最小生成树不唯一
1.Kruskal算法 //O(ElogE)
适合于稀疏图
步骤:
|
证明略
MST性质:具有n个点的带权连通图,其对应的生成图有(n-1)条边
2.Prim算法
适合于稠密图
算法描述:
从单一顶点开始,Prim算法按照以下步骤逐步扩大树中所含顶点的数目,直到遍及连通图的所有顶点。
一.输入:一个加权连通图,其中顶点集合为V,边集为E;
二.初始化:Vnew={x} ,其中x为集合V中的任一节点(起始点),Enew={};
三.重复下列操作,直到Vnew =V;
1.在集合E中选取权值最小的边( u ,v ),其中u为集合Vnew中的元素,而v则不是(如果存在有多条满足前述条件即具有相 同权值的边,则可任意选取其中之一);
2.将v加入集合Vnew中,将(u , v )加入集合Enew中;
四.输出:使用集合Vnew和Enew来描述所得到的最小生成树
图表示为:
时间复杂度
介绍完最小生成树后,介绍次小生成树
1.求出原图的最小生成树,记录权值之和为MST.
2.枚举添加每条不在最小生成树上的边(u ,v) ,加上以后一定会形成一个环。
3.找到环上权值第二大的边(即除了(u ,v)以外的权值最大的边),把它删除,计算当前生成树的权值之和。
4.取所有枚举修改的生成树权值之和的最小值,就是次小生成树。
具体实现方法:
1.从每个节点 i 遍历整个最小生成树,定义F[ i ] 为从 i 到 j 的路径上最大边的权值。
2.遍历图求出F[ i ]的值,然后对于添加每条不在最小生成树中的边(i , j),新的生成树权值之和就是MST + w(i ,j) - F[ i ],记录其最小值,则为次小生成树。
三、单源最短路径
1.Bellman-Ford算法
能在存在负权边的情况下解决最短路问题,模型同样是有向带权图G = (V , E) ,其源点为s, 加权函数为 w: E->R,对该图运行Bellman-Ford 算法后可以返回一个boolean值,表明图中是否存在着一个从源点可达的权为负的回路。
若存在这样的回路的话,返回False,算法说明该问题无解;若不存在这样的回路,返回True,算法将产生最短路径及其权值。此算法采用松弛操作,松弛是改变最短路径和前驱的唯一方式。
首先介绍一下松弛操作,后面的Dijkstra算法以及有向无环图也将用到。不同的是它们对每条边进行一次松弛操作,而Kruskal算法对每条边进行多次松弛操作。
2.Dijkstra算法
时间复杂度:
Dijkstra算法最简单的实现方法是用一个链表或者数组来存储所有顶点的集合Q,所以搜索Q中最小元素的运算只需要线性搜索Q中的所有元素。这样算法的运行时间是O(V^2)
对于边数少于V^2的稀疏图来说,我们可以用邻接表来更有效的实现该算法。同时需要将一个二叉堆或者斐波那契堆用作优先队列来查找最小的顶点。当用到二叉堆的时候,算法所需的时间为O((V + E) log V),斐波那契堆能稍微提高一些性能,让算法运行时间达到O(E + V log V). 然而,使用斐波那契堆进行编程,常常会由于算法常数过大而导致速度没有显著提高。
3.SPFA(Shortest Path Faster Alogrithm)
期望的时间复杂度为O(ke), k 为所有顶点进队的平均次数,可以证明k一般<=2
实现方法:建立一个队列,初始时队列里只有起始点,再建立一个表格记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到它本身的路径赋为0).然后执行松弛操作,用队列里有的点去刷新起始点到所有点的最短路,如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空
判断有无负环:如果某个点进入队列的次数超过N次,则存在负环(存在负环则无最短路径.如果有负环则会无限松弛.而一个带n个点的图至多松弛n-1次).
4.差分约束
如未知量xi , i=1 , 2 , 3 , 4 , 5 .
满足不等式 x1 - x2 <= 0
x1 - x5 <= -1
x2 - x5 <= 1
x3 - x1 <= 5
x4 - x1 <=4
x4 - x3 <= -1
x5 - x3 <= -3
x5 - x4 <=-3
该问题的一个解为x = {-5 , -3 , 0 , -1 , -4} ,差分约束求出来的要么无解,要有有无穷解,如 x = {x1 + t , x2 + t , x3 + t , x4 + t , x5 + t} 同样也是该不等式的解。有解的充要条件是无负权环。
首先构建约束图。即添加一个源点V0, 值为0,指向各顶点的权值为0.为什么权值为0,即构造了x解的范围是<=0的。举个例子,若两数之差均为正数,则得到的解全为0
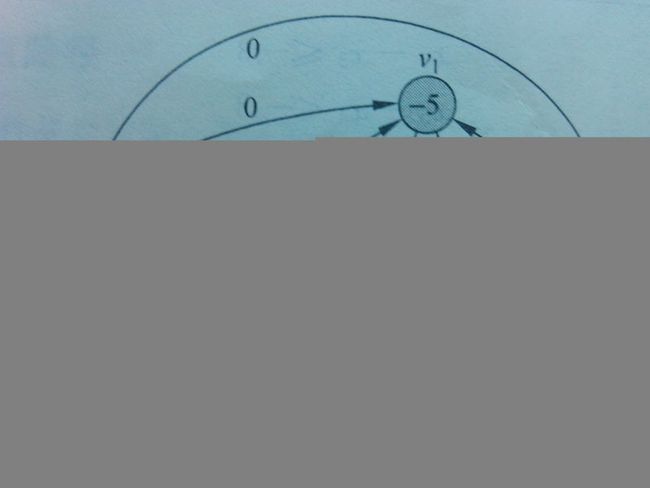
如图,关于n个未知量的m歌约束条件的一个查分约束系统产生出一个具有(n+1)个顶点和(n+m)条边的图,因此采用Bellman-Ford算法,可在O((n+1)(n+m))=O(n^2+nm)时间内将系统解决。若用XXX优化,使其时间变为O(nm),即使m远小于n.待完善————————————
四、每对顶点间的最短路径
1.Floyed-Warshall算法 //时间复杂度O(V^3),空间复杂度O(V^2)
简称Floyed算法,是解决任意两点间的最短路径的一种算法。通常可以在任何图中使用,包括有向图、带负权图的边,同时也被用于计算有向图的传递闭包。它需要邻接矩阵来储存边,这个算法通过考虑最佳子路径来得到最佳路径。
原理:
Floyed算法的原理是动态规划。
设 D ( i , j , k )为从 i 到 j 的只以( 1...k )集合中的节点为中间节点的最短路径的长度。
Ⅰ若最短路径经过点 k, 则 D( i , j , k )= D (i , k , k-1) + D(k , j , k-1);
Ⅱ若最短路径不经过点k,则 D(i , j , k )= D (i , j , k-1).
因此,D (i , j , k) = min { [D(i ,k ,k-1) + D(k , j , k-1)] , D(i , j , k-1)}
如果G中包含边<i , j>,则D(i , j , 0) = 边<i , j>的长度,若i=j,则D(i,j ,0)= 0;
如果G中不包含边<i , j>,则D(i , j , 0)=+∞
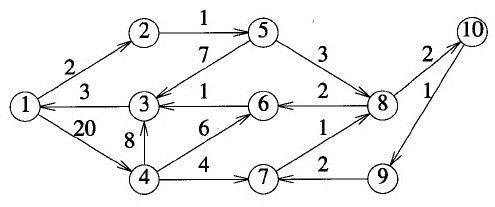
观察上面这个有向图:若k=0, 1 , 2 , 3 , 则D ( 1 , 3 , k )=+∞; D(1, 3 , 4)=28; 若k=5 , 6 , 7 , 则D(1 , 3 , k )=10; 若 k=8 , 9 , 10 , 则D(1 , 3 , k)=9. 因此 1 到 3 的最短路径长度为9
当然,遇到题时可灵活变换,并不一定是加法(减乘除)均可
未完。。。有待完善~~