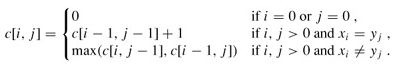动态规划法
经常会遇到复杂问题不能简单地分解成几个子问题,而会分解出一系列的子问题。简单地采用把大问题分解成子问题,并综合子问题的解导出大问题的解的方法,问题求解耗时会按问题规模呈幂级数增加。
为了节约重复求相同子问题的时间,引入一个数组,不管它们是否对最终解有用,把所有子问题的解存于该数组中,这就是动态规划法所采用的基本方法。
【问题】 求两字符序列的最长公共字符子序列
问题描述:字符序列的子序列是指从给定字符序列中随意地(不一定连续)去掉若干个字符(可能一个也不去掉)后所形成的字符序列。令给定的字符序列X=“x0,x1,…,xm-1”,序列Y=“y0,y1,…,yk-1”是X的子序列,存在X的一个严格递增下标序列<i0,i1,…,ik-1>,使得对所有的j=0,1,…,k-1,有xij=yj。例如,X=“ABCBDAB”,Y=“BCDB”是X的一个子序列。
考虑最长公共子序列问题如何分解成子问题,设A=“a0,a1,…,am-1”,B=“b0,b1,…,bm-1”,并Z=“z0,z1,…,zk-1”为它们的最长公共子序列。不难证明有以下性质:
(1) 如果am-1=bn-1,则zk-1=am-1=bn-1,且“z0,z1,…,zk-2”是“a0,a1,…,am-2”和“b0,b1,…,bn-2”的一个最长公共子序列;
(2) 如果am-1!=bn-1,则若zk-1!=am-1,蕴涵“z0,z1,…,zk-1”是“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一个最长公共子序列;
(3) 如果am-1!=bn-1,则若zk-1!=bn-1,蕴涵“z0,z1,…,zk-1”是“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一个最长公共子序列。
这样,在找A和B的公共子序列时,如有am-1=bn-1,则进一步解决一个子问题,找“a0,a1,…,am-2”和“b0,b1,…,bm-2”的一个最长公共子序列;如果am-1!=bn-1,则要解决两个子问题,找出“a0,a1,…,am-2”和“b0,b1,…,bn-1”的一个最长公共子序列和找出“a0,a1,…,am-1”和“b0,b1,…,bn-2”的一个最长公共子序列,再取两者中较长者作为A和B的最长公共子序列。
求解:
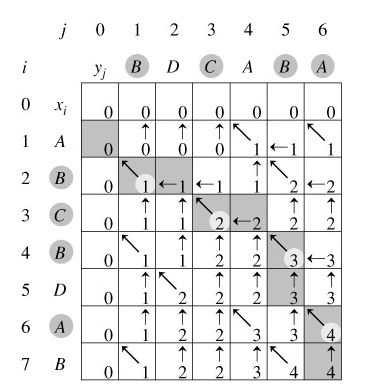
引进一个二维数组c[][],用c[i][j]记录X[i]与Y[j] 的LCS 的长度,b[i][j]记录c[i][j]是通过哪一个子问题的值求得的,以决定搜索的方向。
我们是自底向上进行递推计算,那么在计算c[i,j]之前,c[i-1][j-1],c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j],就可以计算出c[i][j]。
问题的递归式写成:
回溯输出最长公共子序列过程:
算法分析:
由于每次调用至少向上或向左(或向上向左同时)移动一步,故最多调用(m * n)次就会遇到i = 0或j = 0的情况,此时开始返回。返回时与递归调用时方向相反,步数相同,故算法时间复杂度为Θ(m * n)。
Java代码实现:
public class MaxPipei {
public void pipei(char arr1[], char arr2[]) {
int b[][] = new int[arr1.length][arr2.length];
int c[][] = new int[arr1.length][arr2.length];
for (int i = 0; i < arr1.length; i++) {
if (arr1[i] == arr2[0]) {
while (i < arr1.length) {
c[i][0] = 1;
b[i][0] = 1;
i++;
}
} else
c[i][0] = 0;
}
for (int j = 0; j < arr2.length; j++) {
if (arr2[j] == arr1[0]) {
while (j < arr2.length) {
c[0][j] = 1;
b[0][j] = 1;
j++;
}
} else
c[0][j] = 0;
}
for (int i = 1; i < arr1.length; i++) {
for (int j = 1; j < arr2.length; j++) {
if (arr1[i] == arr2[j]) {
c[i][j] = c[i - 1][j - 1] + 1;
b[i][j] = 1;
}
// System.out.println(i + ":" + j);
if (arr1[i] != arr2[j]) {
if (c[i - 1][j] >= c[i][j - 1]) {
c[i][j] = c[i - 1][j];
b[i][j] = 0;
} else if (c[i - 1][j] < c[i][j - 1]) {
c[i][j] = c[i][j - 1];
b[i][j] = -1;
}
}
}
}
System.out.println(c[arr1.length - 1][arr2.length - 1]);
Display(b, arr1, arr1.length - 1, arr2.length - 1);
}
public static void Display(int[][] b, char[] x, int i, int j) {
if (i == -1 || j == -1)
return;
if (b[i][j] == 1) {
Display(b, x, i - 1, j - 1);
System.out.print(x[i] + " ");
} else if (b[i][j] == 0) {
Display(b, x, i - 1, j);
} else if (b[i][j] == -1) {
Display(b, x, i, j - 1);
}
}
public static void main(String[] args) {
MaxPipei maxPipei = new MaxPipei();
maxPipei.pipei("nihaodddiccc".toCharArray(), "hapoii".toCharArray());
}
}
子串如果是连续的,算法如下
import java.util.ArrayList;
import java.util.List;
public class MaxPublicSubString {
List<Integer> maxstr = new ArrayList<Integer>();
int maxLen = Integer.MIN_VALUE;
public void pipei(char arr1[], char arr2[]) {
//同不连续的字符串类似初始化。
int c[][] = new int[arr1.length][arr2.length];
for (int i = 0; i < arr1.length; i++) {
if (arr1[i] == arr2[0]) {
c[i][0] = 1;
} else
c[i][0] = 0;
}
for (int j = 0; j < arr2.length; j++) {
if (arr2[j] == arr1[0]) {
c[0][j] = 1;
} else
c[0][j] = 0;
}
StringBuffer sb = new StringBuffer();
for (int i = 1; i < arr1.length; i++) {
for (int j = 1; j < arr2.length; j++) {
//当前字符相等,则用前面动态规划的值加1,否则为0
c[i][j] = arr1[i] == arr2[j] ? 1 + c[i - 1][j - 1] : 0;
//如果大于最大长度则改变记录位置。
if (c[i][j] > maxLen) {
maxstr.clear();
maxstr.add(i);
maxLen = c[i][j];
} else if (c[i][j] == maxLen) {
maxstr.add(i);
}
}
}
}
public static void main(String[] args) {
String str1 = new String("binghaven");
String str2 = new String("jingseven");
MaxPublicSubString mps = new MaxPublicSubString();
mps.pipei(str1.toCharArray(), str2.toCharArray());
System.out.println(mps.maxLen);
for (Integer i : mps.maxstr) {
System.out.println(str1.substring(i - mps.maxLen + 1, i + 1));
}
}
}