图遍历算法——DFS、BFS、A*、B*和Flood Fill 遍历算法大串讲
图遍历算法——DFS、BFS、A*、B*和Flood Fill 遍历算法大串讲
本文内容框架:
§1 图遍历DFS和BFS两种实现
§2 A*算法
§3 B*算法
§4 Flood Fill算法
§5 小结
图遍历问题分为四类:
遍历完所有的边而不能有重复,即所謂“一笔画问题”或“欧拉路径”;
遍历完所有的顶点而没有重复,即所谓“哈密尔顿问题”。
遍历完所有的边而可以有重复,即所谓“中国邮递员问题”;
遍历完所有的顶点而可以重复,即所谓“旅行推销员问题”。
对于第一和第三类问题已经得到了完满的解决,而第二和第四类问题则只得到了部分解决。
第一类问题就是研究所谓的欧拉图的性质,而第二类问题则是研究所谓的哈密尔顿图的性质。
§1 图遍历DFS和BFS两种实现
图遍历的矩阵存储和邻接表存储的BFS和DFS实现
╔
矩阵存储BFS
#include <stdio.h>
#include <string.h>
#include <queue>
using namespace std;
queue <int> qu, qq;
int map[100][100], m, n, judge[100], path[100];
void bfs(){//和导论上的染色的方法差不多,judge[0] == 0 时候代表白色节点 在队列里面的节点是灰色的 出队列的是黑色的。
int w, s,t,i, j;
while(true){
s = qu.size();
if(!s)return;
while(s--){
t = qu.front();
for(i = 0; i < n; i++){
if(map[t][i] && !judge[i]){
judge[i] = true;
qu.push(i);
path[i] = t;//记录宽度优先搜索树中的当前节点的父亲
//printf("path[%d] = %d\n", i, t);
}
}
qu.pop();
}
}
}
void printpath(int n){ //递归的输出路径
if(path[n] == -1)printf("%d ", n);
else{
printpath(path[n]);
printf("%d ", n);
}
}
int main(){
freopen("bfs.in", "r", stdin);
freopen("bfs.out", "w", stdout);
int i, j, u, v;
while(scanf("%d%d", &n, &m) != -1){
memset(judge, 0, sizeof(judge));
for(i = 0; i < m; i++){
scanf("%d%d", &u, &v);
map[u][v] = map[v][u] = 1;
}
judge[0] = true;qu = qq;
qu.push(0);memset(path, -1, sizeof(path));
bfs();
for(i = 1; i < n; i++){
printf("from 0 to %d : ", i);
printpath(i);puts("");
}
}
return 0;
}
链表存储BFS
#include <stdio.h>
#include <string.h>
#include <queue>
using namespace std;
queue<int> qu, qq;
struct e{
int v;
e* next;
};
e* edge[100];int m, n, judge[100], path[100];
void bfs(){
int w, i, j, t, s;e* l;
while(true){
s = qu.size();
if(!s)return;
while(s--){
w = qu.front();
l = edge[w];
while(l){
t = l->v;
if(!judge[t]){
judge[t] = true;
qu.push(t);
path[t] = w;
}
l = l->next;
}
qu.pop();
}
}
}
void printpath(int x){
if(path[x] == -1)printf("%d ", x);
else{
printpath(path[x]);
printf(" %d", x);
}
}
int main(){ //个人不推荐动态开辟存储空间,建议静态。
freopen("bfs_link.in", "r", stdin);
freopen("bfs_link.out", "w", stdout);
int u, v, i, j;e* node;
while(scanf("%d%d", &n, &m) != -1){
memset(judge, 0, sizeof(judge));
memset(path, -1, sizeof(path));
for(i = 0; i < m; i++){
scanf("%d%d", &u, &v);
node = new e;
node->v = v;
node->next = edge[u];
edge[u] = node;
node = new e;
node->v = u;
node->next = edge[v];
edge[v] = node;
}
judge[0] = true;qu = qq;qu.push(0);
bfs();
for(i = 1; i < n; i++){
printf("path from 0 to %d : ", i);
printpath(i);puts("");
}
}
return 0;
}
矩阵存储DFS
#include <stdio.h>
#include <string.h>
int map[100][100], m, n, d[100], f[100], time, path[100];
bool judge[100];
void dfs(int v){
int i;judge[v] = true;
time++;d[v] = time;//开始时间
for(i = 0; i < n; i++){
if(map[v][i] && !judge[i]){
path[i] = v;//记录深度优先搜索树中的父亲节点
dfs(i);
}
}
time++;f[v] = time;//结束时间
}
void printpath(int v){
if(path[v] == -1)printf("%d ", v);
else{
printpath(path[v]);
printf(" %d", v);
}
}
int main(){
freopen("dfs_m.in", "r", stdin);
freopen("dfs_m.out", "w", stdout);
int i, j, u, v;
while(scanf("%d%d", &n, &m) != -1){
memset(map, 0, sizeof(map));
memset(judge, 0, sizeof(judge));
memset(path, -1, sizeof(path));
for(i = 0; i < m; i++){
scanf("%d%d", &u, &v);
map[u][v] = map[v][u] = true;
}
time = 0;dfs(0);
for(i = 0; i < n; i++){
printf("d[%d] = %d f[%d] = %d\n", i, d[i], i, f[i]);
}
for(i = 1; i < n; i++){
printf("path from 0 to %d : ");
printpath(i);puts("");
}
}
return 0;
}
链表存储BFS
#include <stdio.h>
#include <string.h>
struct e{
int v;
e* next;
};
e* link[100];e edge[10000];//静态的
int m, n, el, judge[100], d[100], f[100], time, path[100];
void dfs(int v){
int i, t;e* l;
judge[v] = true;
time++;d[v] = time;
l = link[v];
while(l){
t = l->v;
if(!judge[t]){
judge[t] = true;
path[t] = v;
dfs(t);
}
l = l->next;
}
time++;f[v] = time;
}
void printpath(int v){
if(path[v] == -1)printf("%d", v);
else{
printpath(path[v]);
printf(" %d", v);
}
}
int main(){
freopen("dfs_link.in", "r", stdin);
freopen("dfs_link.out", "w", stdout);
int i, j, u, v;
while(scanf("%d%d", &n, &m) != -1){
memset(judge, 0, sizeof(judge));
memset(link, 0, sizeof(edge));
memset(path, -1, sizeof(path));
for(i = 0, el = 0; i < m; i++){
scanf("%d%d", &u, &v);
edge[el].v = v;
edge[el].next = link[u];
link[u] = &edge[el++];
edge[el].v = u;
edge[el].next = link[v];
link[v] = &edge[el++];
}time = 0;
for(i = 0; i < n; i++){
if(!judge[i])dfs(i);
}
for(i = 0; i < n; i++){
printf("d[%d] = %d f[%d] = %d\n", i, d[i], i, f[i]);
}
for(i = 1; i < n; i++){
printf("path form 0 to %d : ", i);
printpath(i);puts("");
}
}
return 0;
}
╝①
§2 A*算法
A*算法
A*算法是一种常用的启发式搜索算法。
╔
在A*算法中,一个结点位置的好坏用估价函数来对它进行评估。A*算法的估价函数可表示为:
f'(n) = g'(n) + h'(n)
这里,f'(n)是估价函数,g'(n)是起点到终点的最短路径值(也称为最小耗费或最小代价),h'(n)是n到目标的最短路经的启发值。由于这个f'(n)其实是无法预先知道的,所以实际上使用的是下面的估价函数:
f(n) = g(n) + h(n)
其中g(n)是从初始结点到节点n的实际代价,h(n)是从结点n到目标结点的最佳路径的估计代价。在这里主要是h(n)体现了搜索的启发信息,因为g(n)是已知的。用f(n)作为f'(n)的近似,也就是用g(n)代替g'(n),h(n)代替h'(n)。这样必须满足两个条件:(1)g(n)>=g'(n)(大多数情况下都是满足的,可以不用考虑),且f必须保持单调递增。(2)h必须小于等于实际的从当前节点到达目标节点的最小耗费h(n)<=h'(n)。第二点特别的重要。可以证明应用这样的估价函数是可以找到最短路径的。
A*算法的具体步骤
A*算法基本上与广度优先算法相同,但是在扩展出一个结点后,要计算它的估价函数,并根据估价函数对待扩展的结点排序,从而保证每次扩展的结点都是估价函数最小的结点。
1)建立一个队列,计算初始结点的估价函数f,并将初始结点入队,设置队列头和尾指针。
2)取出队列头(队列头指针所指)的结点,如果该结点是目标结点,则输出路径,程序结束。否则对结点进行扩展。
3)检查扩展出的新结点是否与队列中的结点重复,若与不能再扩展的结点重复(位于队列头指针之前),则将它抛弃;若新结点与待扩展的结点重复(位于队列头指针之后),则比较两个结点的估价函数中g的大小,保留较小g值的结点。跳至第五步。
4)如果扩展出的新结点与队列中的结点不重复,则按照它的估价函数f大小将它插入队列中的头结点后待扩展结点的适当位置,使它们按从小到大的顺序排列,最后更新队列尾指针。
5)如果队列头的结点还可以扩展,直接返回第二步。否则将队列头指针指向下一结点,再返回第二步。
╝②
A*算法图解
╔
如图所示简易地图, 其中绿色方块的是起点 (用 A 表示), 中间蓝色的是障碍物, 红色的方块 (用 B 表示) 是目的地. 为了可以用一个二维数组来表示地图, 我们将地图划分成一个个的小方块。
二维数组在游戏中的应用是很多的, 比如贪吃蛇和俄罗斯方块基本原理就是移动方块而已. 而大型游戏的地图, 则是将各种"地貌"铺在这样的小方块上。
G 表示从起点 A 移动到网格上指定方格的移动耗费 (可沿斜方向移动)。
H 表示从指定的方格移动到终点 B 的预计耗费 (H 有很多计算方法, 这里我们设定只可以上下左右移动)。
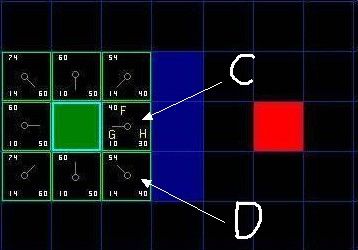
我们假设横向移动一个格子的耗费为10, 为了便于计算, 沿斜方向移动一个格子耗费是14. 为了更直观的展示如何运算 F,G,H, 图中方块的左上角数字表示 F, 左下角表示 G, 右下角表示 H。 看看上图是否跟你心里想的结果一样?

将上图A周围的方块全部放入队列,取出F值最小的方块C,看看 C 下面的那个格子, 它目前的 G 是14, 如果通过 C 到达它的话, G将会是 10 + 10, 这比 14 要大, 因此我们什么也不做(上面步骤3))。

以C为中心结点,扩展新结点 ,并进入队列(上面步骤4))。

直到最终找到终点B,上面浅蓝色边缘的方块是移动过的地点(实际走过的地方),浅绿色边缘的方块是还在队列中的方块。
╝③
A*算法实现
╔
/*
* file: astar_algorithm.h
* author: MulinB@HUST
* date: 2010-10-10
* modified: 2012-05-09
* A-star algorithm implemented in C. Only for study.
*/
#ifndef _ASTAR_ALGORITHM_H
#define _ASTAR_ALGORITHM_H
#include <math.h>
#define M 6
#define N 8
//map marks
#define AVAIL 0
#define UNAVAIL -1
#define START 100
#define END 111
#define ROAD 10
#define GET_F(X) (X->G + X->H)
typedef struct Node
{
//for node itself
int type; //node type
int i; //i index
int j; //j index
//for A star algorithm
double G; //past road cost
double H; //heuristic, F = G + H
struct Node* parent; //parent node, used for trace road
struct Node* next; //only used for open and close list
}Node;
//==========================open close list operation================
Node* open_list;
Node* close_list;
void init_openlist()
{
open_list = NULL;
}
void init_closelist()
{
close_list = NULL;
}
void destroy_openlist()
{
Node* q;
Node* p = open_list;
while (p != NULL)
{
q = p->next;
free(p);
p = q;
}
}
void destroy_closelist()
{
Node* q;
Node* p = close_list;
while (p != NULL)
{
q = p->next;
free(p);
p = q;
}
}
void insert_into_openlist(Node* new_node) //insert and sort by F
{
Node* p;
Node* q;
if (open_list == NULL)
{
open_list = new_node; //insert as the first
return;
}
p = open_list;
while (p != NULL)
{
q = p;
p = p->next;
if (p == NULL)
{
q->next = new_node; //insert as the last
return;
}
else if (GET_F(new_node) < GET_F(p))
{
q->next = new_node; //insert before p, sorted
new_node->next = p;
return;
}
}
}
void insert_into_closelist(Node* new_node) //just insert before head
{
if (close_list == NULL)
{
close_list = new_node; //insert as the first
return;
}
else
{
new_node->next = close_list; //insert before head
close_list = new_node;
return;
}
}
Node* find_node_in_list_by_ij(Node* node_list, int di, int dj)
{
Node* p = node_list;
while (p)
{
if (p->i == di && p->j == dj)
return p;
p = p->next;
}
return NULL;
}
Node* pop_firstnode_from_openlist() //get the minimum node sorted by F
{
Node* p = open_list;
if (p == NULL)
{
return NULL;
}
else
{
open_list = p->next;
p->next = NULL;
return p;
}
}
void remove_node_from_openlist(Node* nd) //just remove it, do not destroy it
{
Node* q;
Node* p = open_list;
if (open_list == nd)
{
open_list = open_list->next;
return;
}
while (p)
{
q = p;
p = p->next;
if (p == nd) //found
{
q->next = p->next;
p->next = NULL;
return;
}
}
}
void remove_node_from_closelist(Node* nd) //just remove it, do not destroy it
{
Node* q;
Node* p = close_list;
if (close_list == nd)
{
close_list = close_list->next;
return;
}
while (p)
{
q = p;
p = p->next;
if (p == nd) //found
{
q->next = p->next;
p->next = NULL;
return;
}
}
}
//===================================================================
//=======================calculate H, G =============================
//calculate Heuristic value
//(reimplemented when porting a star to another application)
double calc_H(int cur_i, int cur_j, int end_i, int end_j)
{
return (abs(end_j - cur_j) + abs(end_i - cur_i)) * 10.0; //the heuristic
}
//calculate G value
//(reimplemented when porting a star to another application)
double calc_G(Node* cur_node)
{
Node* p = cur_node->parent;
if (abs(p->i - cur_node->i) + abs(p->j - cur_node->j) > 1)
return 14.0 + p->G; //the diagonal cost is 14
else
return 10.0 + p->G; //the adjacent cost is 10
}
void init_start_node(Node* st, int si, int sj, int ei, int ej)
{
memset(st, 0, sizeof(Node));
st->type = START;
st->i = si;
st->j = sj;
st->H = calc_H(si, sj, ei, ej);
st->G = 0;
}
void init_end_node(Node* ed, int ei, int ej)
{
memset(ed, 0, sizeof(Node));
ed->type = END;
ed->i = ei;
ed->j = ej;
ed->H = 0;
ed->G = 9999; //temp value
}
void init_pass_node(Node* pd, int pi, int pj)
{
memset(pd, 0, sizeof(Node));
pd->type = AVAIL;
pd->i = pi;
pd->j = pj;
}
//check the candidate node (i,j) when extending parent_node
int check_neighbor(int map[][N], int width, int height,
int di, int dj, Node* parent_node, Node* end_node)
{
Node* p;
Node* temp;
double new_G;
if (di < 0 || dj < 0 || di > height-1 || dj > width-1)
return UNAVAIL;
//1. check available
if (map[di][dj] == UNAVAIL)
return UNAVAIL;
//2. check if existed in close list
p = find_node_in_list_by_ij(close_list, di, dj);
if (p != NULL)
{
//found in the closed list, check if the new G is better, added 2012-05-09
temp = p->parent;
p->parent = parent_node;
new_G = calc_G(p);
if (new_G >= p->G)
{
p->parent = temp; //if new_G is worse, recover the parent
}
else
{
//the new_G is better, remove it from close list, insert it into open list
p->G = new_G;
remove_node_from_closelist(p); //remove it
insert_into_openlist(p); //insert it, sorted
}
return AVAIL;
}
//3. check if existed in open list
p = find_node_in_list_by_ij(open_list, di, dj); //in open list
if (p != NULL)
{
//found in the open list, check if the new G is better
temp = p->parent;
p->parent = parent_node;
new_G = calc_G(p);
if (new_G >= p->G)
{
p->parent = temp; //if new_G is worse, recover the parent
}
else
{
//the new_G is better, resort the list
p->G = new_G;
remove_node_from_openlist(p); //remove it
insert_into_openlist(p); //insert it, sorted
}
return AVAIL;
}
//4. none of above, insert a new node into open list
if (map[di][dj] == END)
{
//4~. check if it is end node
end_node->parent = parent_node;
end_node->G = calc_G(end_node);
insert_into_openlist(end_node); //insert into openlist
return AVAIL;
}
else
{
//4~~. create a new node
p = malloc(sizeof(Node));
init_pass_node(p, di, dj);
p->parent = parent_node;
p->H = calc_H(di, dj, end_node->i, end_node->j);
p->G = calc_G(p);
insert_into_openlist(p); //insert into openlist
return AVAIL;
}
}
//extend the current node on the map
//(reimplemented when porting a star to another application)
void extend_node(Node* cd, int map[][N], int width, int height, Node* end_node)
{
int up_status, down_status, left_status, right_status;
int ci, cj; //cur node i, j
int ti, tj; //temp i, j
ci = cd->i;
cj = cd->j;
//1. up
ti = ci - 1;
tj = cj;
up_status = check_neighbor(map, width, height, ti, tj, cd, end_node);
//2. down
ti = ci + 1;
tj = cj;
down_status = check_neighbor(map, width, height, ti, tj, cd, end_node);
//3. left
ti = ci;
tj = cj - 1;
left_status = check_neighbor(map, width, height, ti, tj, cd, end_node);
//4. right
ti = ci;
tj = cj + 1;
right_status = check_neighbor(map, width, height, ti, tj, cd, end_node);
//5. leftup
ti = ci - 1;
tj = cj - 1;
if (up_status == AVAIL && left_status == AVAIL)
check_neighbor(map, width, height, ti, tj, cd, end_node);
//6. rightup
ti = ci - 1;
tj = cj + 1;
if (up_status == AVAIL && right_status == AVAIL)
check_neighbor(map, width, height, ti, tj, cd, end_node);
//7. leftdown
ti = ci + 1;
tj = cj - 1;
if (down_status == AVAIL && left_status == AVAIL)
check_neighbor(map, width, height, ti, tj, cd, end_node);
//8. rightdown
ti = ci + 1;
tj = cj + 1;
if (down_status == AVAIL && right_status == AVAIL)
check_neighbor(map, width, height, ti, tj, cd, end_node);
}
//=======================search algorithm======================================
/*
A*方法总结 (from http://www.policyalmanac.org/games/aStarTutorial.htm):
1. 把起始格添加到开启列表。
2. 重复如下的工作:
a) 寻找开启列表中F值最低的格子。我们称它为当前格。
b) 把它切换到关闭列表。
c) 对相邻的8格中的每一个?
* 如果它不可通过或者已经在关闭列表中,略过它。反之如下。(MulinB 2012-05-09 按:在关闭列表中是否也应该检查它,看是否可以获得更低的G值?? ref: http://theory.stanford.edu/~amitp/GameProgramming/ImplementationNotes.html )
* 如果它不在开启列表中,把它添加进去。把当前格作为这一格的父节点。记录这一格的F,G,和H值。
* 如果它已经在开启列表中,用G值为参考检查新的路径是否更好。更低的G值意味着更好的路径。
如果是这样,就把这一格的父节点改成当前格,并且重新计算这一格的G和F值。
如果你保持你的开启列表按F值排序,改变之后你可能需要重新对开启列表排序。
d) 停止,当你
* 把目标格添加进了关闭列表(注解),这时候路径被找到,或者
* 没有找到目标格,开启列表已经空了。这时候,路径不存在。
3. 保存路径。从目标格开始,沿着每一格的父节点移动直到回到起始格。这就是你的路径。
*/
//search a road on a map, return node_list
Node* a_star_search(int map[M][N], int width, int height,
int start_i, int start_j, int end_i, int end_j)
{
Node* cur_node;
Node* start_node;
Node* end_node;
//create start and end node
start_node = malloc(sizeof(Node));
init_start_node(start_node, start_i, start_j, end_i, end_j);
end_node = malloc(sizeof(Node));
init_end_node(end_node, end_i, end_j);
//init open and close list
init_openlist();
init_closelist();
//put start_node into open list
insert_into_openlist(start_node);
//start searching
while (1)
{
cur_node = pop_firstnode_from_openlist(); //it has the minimum F value
if (cur_node == NULL || cur_node->type == END)
{
break; //found the road or no road found
}
extend_node(cur_node, map, width, height, end_node); //the key step!!
insert_into_closelist(cur_node);
}
//you can track the road by the node->parent
return cur_node;
}
#endif /* file end */
╝④
B*算法
╔
B* 寻路算法又叫Branch Star 分支寻路算法,且与A*对应,本算法适用于游戏中怪物的自动寻路,其效率远远超过A*算法,经过测试,效率是普通A*算法的几十上百倍。
通过引入该算法,一定程度上解决了游戏服务器端无法进行常规寻路的效率问题,除非服务器端有独立的AI处理线程,否则在服务器端无法允许可能消耗大量时间的寻路搜索,即使是业界普遍公认的最佳的A*,所以普遍的折中做法是服务器端只做近距离的寻路,或通过导航站点缩短A*的范围。
§3 B*算法
B*算法原理
本算法启发于自然界中真实动物的寻路过程,并加以改善以解决各种阻挡问题(有点类似蚁群算法)。
前置定义:
1、探索节点:
为了叙述方便,我们定义在寻路过程中向前探索的节点(地图格子)称为探索节点,起始探索节点即为原点。(探索节点可以对应为A*中的开放节点)。
2、自由的探索节点:
探索节点朝着目标前进,如果前方不是阻挡,探索节点可以继续向前进入下一个地图格子,这种探索节点我们称为自由探索节点;
3、绕爬的探索节点:
探索节点朝着目标前进,如果前方是阻挡,探索节点将试图绕过阻挡,绕行中的探索节点我们成为绕爬的探索节点;
B*算法流程
1、起始,探索节点为自由节点,从原点出发,向目标前进;
2、自由节点前进过程中判断前面是否为障碍,
a、不是障碍,向目标前进一步,仍为自由节点;
b、是障碍,以前方障碍为界,分出左右两个分支,分别试图绕过障碍,这两个分支节点即成为两个绕爬的探索节点;
3、绕爬的探索节点绕过障碍后,又成为自由节点,回到2);
4、探索节点前进后,判断当前地图格子是否为目标格子,如果是则寻路成功,根据寻路过程构造完整路径;
5、寻路过程中,如果探索节点没有了,则寻路结束,表明没有目标格子不可达;
B*算法图解演示


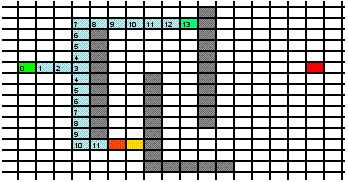

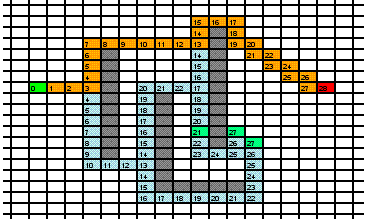
B*算法与A*算法的性能比较
寻路次数比较(5秒钟寻路次数)

╝⑤
§4 Flood Fill算法
Flood Fill算法
Flood Fill算法是计算机图形学和数字图像处理的一个填充算法,其实就是从一点开始向四面周围寻找点填充遍历,原理和BFS很相似,当然也可以像DFS一样的遍历。
Flood Fill 算法图解演示
Flood Fill算法实现
说的Flood Fill算法的实现不得不提Lode's Computer Graphics Tutorial。该算法可以通过递归或者是stack来完成,下面只附上4-Way Recurisive Method:
//Recursive 4-way floodfill, crashes if recursion stack is full
void floodFill4(int x, int y, int newColor, int oldColor)
{
if(x >= 0 && x < w && y >= 0 && y < h && screenBuffer[x][y] == oldColor && screenBuffer[x][y] != newColor)
{
screenBuffer[x][y] = newColor; //set color before starting recursion
floodFill4(x + 1, y, newColor, oldColor);
floodFill4(x - 1, y, newColor, oldColor);
floodFill4(x, y + 1, newColor, oldColor);
floodFill4(x, y - 1, newColor, oldColor);
}
}
§5 小结
这篇文章摘录了图算法最基本的BFS和DFS的实现以及A*、B*和Flood Fill的基本原理,由于原理不是十分难懂又有图解过程,所以可以一次性掌握原理(虽然文字介绍相当简要,不过好像也没有什么要说的),剩下的动手的问题。如果你有任何建议或者批评和补充,请留言指出,不胜感激,更多参考请移步互联网。
参考:
①MemoryGarden: http://www.cppblog.com/MemoryGarden/articles/97979.html
②阿凡卢: http://www.cnblogs.com/luxiaoxun/archive/2012/08/05/2624115.html
③ Create Chen: http://www.cnblogs.com/technology/archive/2011/05/26/2058842.html
④在迷茫中寻找四叶草 --MulinB的技术博客: http://blog.csdn.net/mulinb/article/details/5939225
⑤inysong: http://qinysong.iteye.com/blog/678941


