Geometric Search

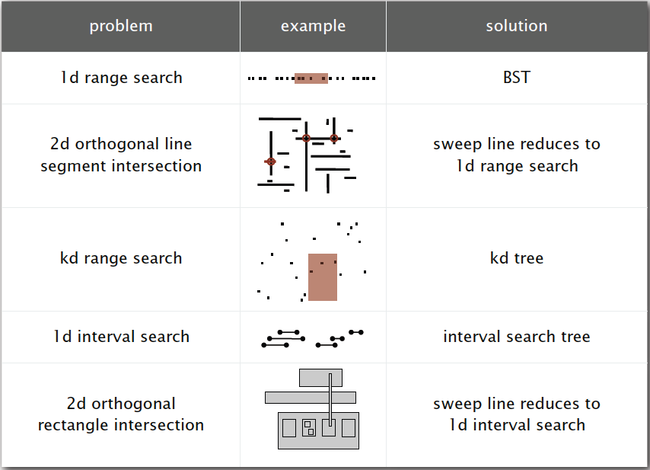
1.  1d range search

    --  Range search: find all keys between k1 and k2.

    --  Range count: number of keys between k1 and k2.

    --  BST Implementation of range count: rank(k) -- number of keys < k (Running time : O(logN)

 

public int size(Key lo, Key hi)
{
    if (contains(hi)) return rank(hi) - rank(lo) + 1;
    else return rank(hi) - rank(lo);
}

    --  BST Implementation of range search: (Running time : O(R + NlogN)

        -- Recursively find all keys in left subtree (if any could fall in range).

        -- Check key in current node.

        -- Recursively find all keys in right subtree (if any could fall in range).

  

 

 

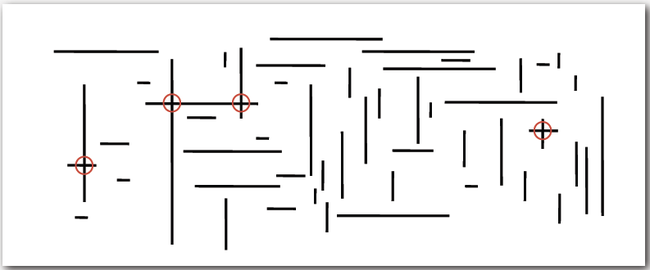
2.  Orthogonal line segment intersection

    --  Given N horizontal and vertical line segments, find all intersections.

    --  Assumption: All x- and y-coordinates are distinct.

 

3.  Sweep-line Algorithm

    --  Algorithm:

        --  x-coordinates define events.

        --  h-segment (left endpoint): insert y-coordinate into BST.

        --  h-segment (right endpoint): remove y-coordinate from BST.

        --  v-segment: range search for interval of y-endpoints.

    --  Running Time:

        --  Put x-coordinates on a PQ (or sort).    ---- N log N

        --  Insert y-coordinates into BST.    ---- N log N

        --  Delete y-coordinates from BST.    ---- N log N

        --  Range searches in BST.    ---- N log N + R

    --  Reduces 2d orthogonal line segment intersection search to 1d range search.

 

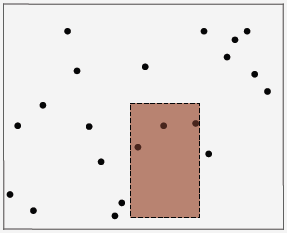
4.  2-d orthogonal range search:

    --  Extension of ordered symbol-table to 2d keys.

        --  Insert a 2d key.

        --  Delete a 2d key.

        --  Search for a 2d key.

        --  Range search: find all keys that lie in a 2d range.

        --  Range count: number of keys that lie in a 2d range.

    --  Geometric interpretation.

        --  Keys are point in the plane.

        --  Find/count points in a given horizontal-vertical rectangle

 

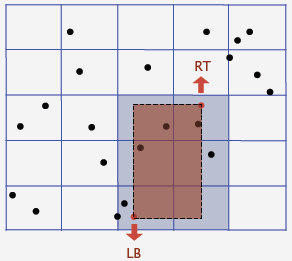
5.  Grid implementation

    --  Algorithm

        --  Divide space into M-by-M grid of squares.

        --  Create list of points contained in each square.

        --  Use 2d array to directly index relevant square.

        --  Insert: add (x, y) to list for corresponding square.

        --  Range search: examine only squares that intersect 2d range query.

    --  Space-time tradeoff.

        --  Space: M^2 + N.

        --  Time: 1 + N / M^2 per square examined, on average.

        --  Grid square size too small: wastes space.

        --  Grid square size too large: too many points per square.

        --  Rule of thumb: √N-by-√N grid.

    --  Running time. [if points are evenly distributed and M ~ √N ]

        --  Initialize data structure: N.

        --  Insert point: 1.

        --  Range search: 1 per point in range.

    --  Clustering : a well-known phenomenon in geometric data.

        --  Lists are too long, even though average length is short.

        --  Need data structure that adapts gracefully to data.

 
 

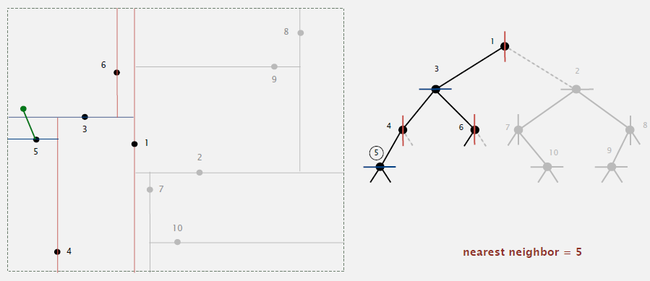
 6.  Space-partitioning trees:

    --  Use a tree to represent a recursive subdivision of 2d space.

    --  Implementation : BST, but alternate using x- and y-coordinates as key.

        --  Search gives rectangle containing point.

        --  Insert further subdivides the plane.

    --  Range search in a 2d tree : (Running time : typical case : R + log N , worst case : R + √N)

        --  Check if point in node lies in given rectangle.

        --  Recursively search left/bottom (if any could fall in rectangle).

        --  Recursively search right/top (if any could fall in rectangle).

 
      --  Nearest neighbor search in a 2d tree : (Running time : typical case : log N , worst case : N)

        --  Check distance from point in node to query point.

        --  Recursively search left/bottom (if it could contain a closer point).

        --  Recursively search right/top (if it could contain a closer point).

        --  Organize method so that it begins by searching for query point.

 

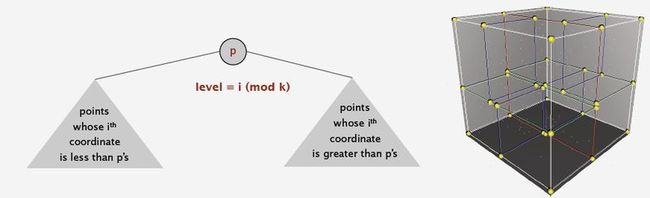
7.  Kd tree  ----  Recursively partition k-dimensional space into 2 halfspaces.

    --  Implementation: BST, but cycle through dimensions ala 2d trees.

 

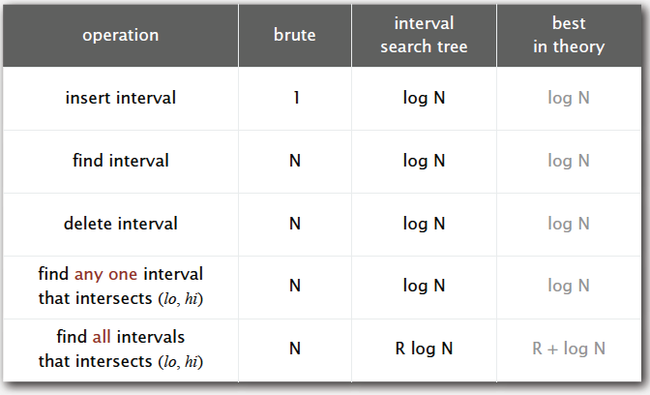
8.  1d interval search

    --  Data structure to hold set of (overlapping) intervals.

    --  Insert an interval ( lo, hi ).

    --  Search for an interval ( lo, hi ).

    --  Delete an interval ( lo, hi ).

    --  Interval intersection query: given an interval ( lo, hi ), find all intervals in data structure overlapping ( lo, hi ).

 

9.  Interval search trees

    --  Create BST, where each node stores an interval ( lo, hi ).

        --  Use left endpoint as BST key.

        --  Store max endpoint in subtree rooted at node.

    --  To insert an interval ( lo, hi ) :

        --  Insert into BST, using lo as the key.

        --  Update max in each node on search path.

    --  To search for any one interval that intersects query interval ( lo, hi ) :

        --  If interval in node intersects query interval, return it.

        --  Else if left subtree is null, go right.

        --  Else if max endpoint in left subtree is less than lo, go right.

        --  Else go left.

    --  Running Time :

 

10.  Proof of correctness of Interval Search :

    --  Case 1. If search goes right, then no intersection in left.

        --  Left subtree is empty ⇒ trivial.

        --  Max endpoint max in left subtree is less than lo ⇒ for any interval (a, b) in left subtree of x, we have b ≤ max < lo.

    --  Case 2. If search goes left, then there is either an intersection in left subtree or no intersections in either.

        --  Suppose no intersection in left. Since went left, we have lo ≤ max. Then for any interval (a, b) in right subtree of x, hi < c ≤ a where c is the left endpoint of interval with max right endpoint ⇒ no intersection in right.

 

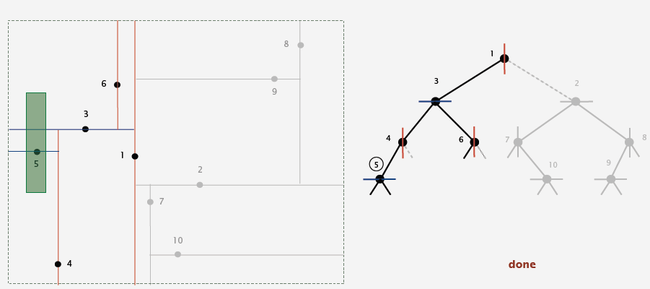
11.  Orthogonal rectangle intersection:

    --  Goal. Find all intersections among a set of N orthogonal rectangles.

    --  Sweep Line Algorithm:

        --  Sweep vertical line from left to right.

        --  x-coordinates of left and right endpoints define events.

        --  Maintain set of rectangles that intersect the sweep line in an interval search tree (using y-intervals of rectangle).

        --  Left endpoint: interval search for y-interval of rectangle: insert y-interval.

        --  Right endpoint: remove y-interval.

    --  Running Time :

        --  Put x-coordinates on a PQ (or sort).    ----  N log N

        --  Insert y-intervals into ST.    ----  N log N

        --  Delete y-intervals from ST.    ----  N log N

        --  Interval searches for y-intervals.    ----  N log N + R log N

    -- Reduces 2d orthogonal rectangle intersection search to 1d interval search.

 

12.  Summary: