简介
最早碰到这个问题是在读大学刚开始学数据结构的时候。还记得当年为了验证自己的一种思路连续调试了好几天,最后虽然得出了一个结果,不过算法的时间复杂度达到了O(n^3)。现在回顾起来挺有意思的。
问题分析
Josephus环的问题看起来很简单,假设有n个人排成一个圈。从第一个人开始报数,数到第m个人的时候这个人从队列里出列。然后继续在环里数后面第m个人,让其出列直到所有人都出列。求所有这些人出列的排列顺序。
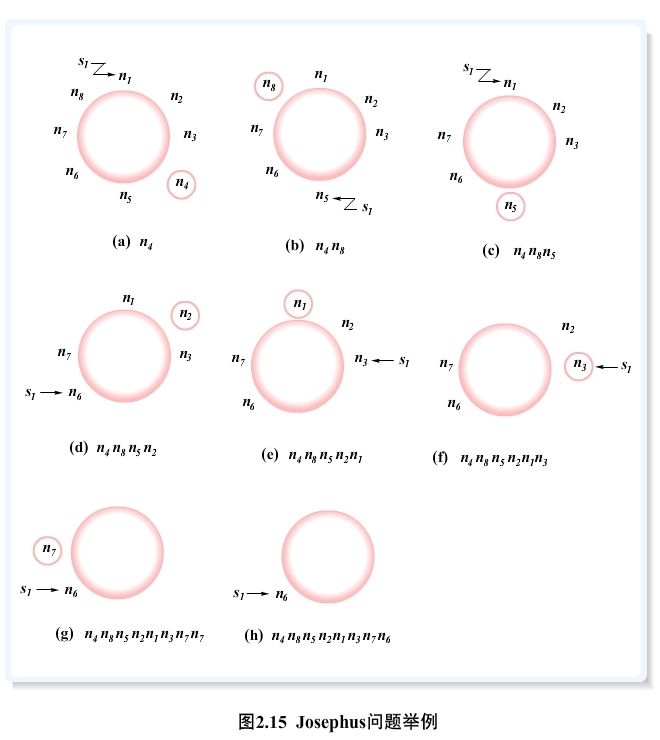
一个典型的示例如下图所示:
在上图中,我们从n1元素开始顺时针数到第4个元素,然后n4号出列。这样,我们就剩下了7个元素。我们在剩下的元素里按照原来顺序继续数到后面4个。这样一直下去,我们可以看到依次找到的出列元素为n4,n8,n5,n2,n1,n3,n7,n6。
解法一: 队列
一种方法是我们可以使用队列。怎么来处理呢?因为我们每次都是处理n个元素里第m个元素。如果我们每次从队列里一边取元素,一边又加入到队列的末尾,直到数到第m的时候。这个第m的元素直接让它移除,我们就保证了取到恰当的元素,同时又保证原来环的顺序没有改变。这样一直循环n遍,我们就可以将所有元素都取出来了。从前面讨论的过程我们就可以看到,它的时间复杂度为O(m*n)。
一个参考的代码实现如下:
import java.util.Queue;
import java.util.ArrayDeque;
public class Josephus<T> {
private Queue<T> queue;
public Josephus(int length) {
if(length <= 0)
throw new IllegalArgumentException("Invalid length!");
queue = new ArrayDeque<T>(length);
}
public void process(int interval) {
if(interval <= 0)
throw new IllegalArgumentException("Invalid interval");
int length = queue.size();
for(int i = 0; i < length; i++) {
for(int j = 0; j < interval; j++) {
T t = queue.remove();
queue.add(t);
}
T removed = queue.remove();
System.out.println(removed);
}
}
public void add(T t) {
queue.add(t);
}
public static void main(String[] args) {
Josephus<Integer> josephus = new Josephus<Integer>(7);
josephus.add(1);
josephus.add(2);
josephus.add(3);
josephus.add(4);
josephus.add(5);
josephus.add(6);
josephus.add(7);
josephus.process(3);
}
}
这里的方法借用了jdk里默认自带的队列。算是稍微取了一点巧。
解法二:循环链表
这一种思路和前面的很近似,就是使用一个循环链表,然后每次数到给定的数字m时删除这个指定的元素。在jdk里的LinkedList就是一个这样的典型数据结构。整体的过程伪代码实现如下:
public static void process(LinkedList list, int m, int n) {
Node node = list.first;
for(int i = 0; i < n; i++) {
for(int j = 0; j < m; j++) {
node = node.next;
}
System.out.println(node);
list.remove(node);
}
}
另外一种思路
前面那两种思路看起来比较简单直接,可是从另外一个角度来看觉得似乎思考的深度不够。既然是一个n人的环,然后每次到第m个的时候就去掉。这样的数学过程是不是有一个数学层面的规律可循呢?如果这样的问题可以通过一个简单的数学公式就可以解决的话,那岂不是更好?让我们先将问题稍微简化一点。假定我们不考虑他们顺序移除的元素,就考虑移除某一个元素之后他们之间的对应关系。
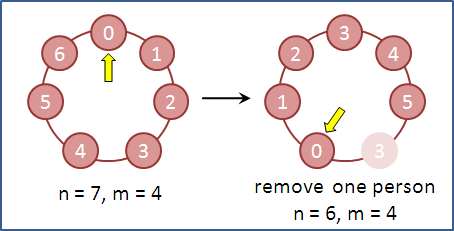
我们来看下图:
对于一个长度为7的环,我们走的步长是4。在走过4步之后我们找到3这个元素,并将它出队。然后我们在3后面的元素,4开始继续下一个查找步骤。而实际上我们从这个时候开始,不正是从n-1个元素里开始取元素了吗?因此我们可以将这个下一步取元素的问题归结为从n-1个元素里取下一个。不过,在上面的示例中,我们是在走到应该为4的元素那里重新以元素0开始作为n-1个元素取下一个的基础。因此,他们之间还存在着一个转换的关系。
我们再从一个更加一般的场景来考虑。在第一个人出队之后,这个第一个出队的人的编号必然为(m - 1) % n。剩下的n-1个人组成一个新的Josephus环。只是这个时候我们是以m % n开始。假定k = m % n。他们组成一个这样的序列:
k, k+1, k+2...n-2, n-1, 0, 1, ... k-2。这个序列中缺少的k-1恰好就是我们前面一次遍历的时候找到并移除的。在我们将他们归结为n-1规模的Josephus环时,我们对他们有了这么一个映射:
k --> 0
k+1 --> 1
k+2 --> 2
...
...
k-3 --> n-3
k-2 --> n-2
这说明了一个什么问题呢?这说明对于我们在n-1的环中,任何一个元素的index对应到n的环中时他们之间差了k,也就是m % n。而这里的差不是一个简单的小于,而是由于整个环的结构,相当于一个循环进位的效果。这样,既然我们在n - 1对应到n的环中间是差了m % n,在更加一般的情况下,任何一个长度为l的环的元素对应到l +1的环的index都是差了这么个m % l。
现在到了问题的关键点了。我们在一个n长的环里取m的步长,然后这个环里少了一个。剩下的n-1个元素构成了n-1环。而这里的元素和n长的元素之间的映射关系是Index(n) = (Index(n - 1) + m) % n。而如果我们载往下一步移除元素呢,他们之间的关系则是Index(n - 1) = (Index(n - 2) + m) % (n - 1)。哈哈,有意思,我们好像找到点规律了。没错,按照刚才的过程,我们这样一直移除元素下去,肯定能够找到最后一个被移除的元素。这个元素则对应只有一个元素的环,很显然,它的值为0。也就是Index(1) = 0。对于这个元素的索引,它对应两个元素的索引是多少呢?按照前面的过程,我们倒推回去就是了。Index(2) = (Index(1) + m) % 2。那么对应3个,4个元素的呢?我们这样一路继续下去就可以找到对应到n个元素的索引了。所以,我们发现了一个有意思的数学归纳关系:
f(1) = 0, f(n) = (f(n - 1) + m) % n。
按照这个关系,我们可以得到最后一个被取出来的元素对应到n个元素的环里的索引值。按照这个公式,我们可以定义出如下的代码:
public static void simulate(int n, int m) {
int answer = 0;
for(int i = 1; i <= n; i++) {
answer = (answer + m) % i;
System.out.println("Survival: " + answer);
}
}
运行这段代码的输出如下:
Survival: 0 Survival: 1 Survival: 1 Survival: 0 Survival: 3 Survival: 0 Survival: 3
这里最有意思的就是里面输出的每个数字都是对应到不同长度的索引值。 比如这里我们对应的7个元素里,最后一个被选择到的在索引为3的那个位置。这就是数学的力量啊,真美!
总结
Josephus环问题是一个很老的问题了。从10多年前碰到它,自己用一种很笨拙的方式去解决它,到现在考虑的用队列和循环链表解决,以及考虑相关的数学关系。我们可以发现一些看似简单的问题其实蕴含着很深层次的数学之美。在一些元素位置的推导方面目前自己还有一些地方理解的不够完善,后续还会继续补充说明。
参考材料
http://comicmimiboy.blog.163.com/blog/static/1511582702011729102428974/