【OpenCV】SIFT原理与源码分析：DoG尺度空间构造

《SIFT原理与源码分析》系列文章索引：http://blog.csdn.net/xiaowei_cqu/article/details/8069548

尺度空间理论

自然界中的物体随着观测 尺度不同有不同的表现形态。例如我们形容建筑物用“米”，观测分子、原子等用“纳米”。更形象的例子比如 Google地图，滑动鼠标轮可以改变观测地图的尺度，看到的地图绘制也不同；还有电影中的拉伸镜头等等……

尺度空间中各尺度图像的模糊程度逐渐变大，能够模拟人在距离目标由近到远时目标在视网膜上的形成过程。
尺度越大图像越模糊。

为什么要讨论尺度空间？

用机器视觉系统分析未知场景时，计算机并不预先知道图像中物体的尺度。我们需要同时考虑图像在多尺度下的描述，获知感兴趣物体的 最佳尺度。另外如果不同的尺度下都有同样的关键点，那么在不同的尺度的输入图像下就都可以检测出来关键点匹配，也就是 尺度不变性。

图像的尺度空间表达就是图像在所有尺度下的描述。

 

尺度空间表达与金字塔多分辨率表达

 

高斯模糊

高斯核是唯一可以产生多尺度空间的核（《Scale-space theory: A basic tool for analysing structures at different scales》）。一个图像的尺度空间L(x,y,σ) ,定义为原始图像I(x,y)与一个可变尺度的2维高斯函数G(x,y,σ)卷积运算。

二维空间高斯函数：

尺度空间：

尺度是自然客观存在的，不是主观创造的。高斯卷积只是表现尺度空间的一种形式。

二维空间高斯函数是等高线从中心成正太分布的同心圆：

 

 

分布不为零的点组成卷积阵与原始图像做变换，即每个像素值是周围相邻像素值的高斯平均。一个5*5的高斯模版如下所示：

 

 

高斯模版是圆对称的，且卷积的结果使原始像素值有最大的权重，距离中心越远的相邻像素值权重也越小。
在实际应用中，在计算高斯函数的离散近似时，在大概3σ距离之外的像素都可以看作不起作用，这些像素的计算也就可以忽略。所以，通常程序只计算(6σ+1)*(6σ+1)就可以保证相关像素影响。

高斯模糊另一个很厉害的性质就是线性可分：使用二维矩阵变换的高斯模糊可以通过在水平和竖直方向各进行一维高斯矩阵变换相加得到。

O(N^2*m*n)次乘法就缩减成了O(N*m*n)+O(N*m*n)次乘法。（N为高斯核大小，m,n为二维图像高和宽）

其实高斯这一部分只需要简单了解就可以了，在OpenCV也只需要一句代码：

 

GaussianBlur(dbl, dbl, Size(), sig_diff, sig_diff);

我这里详写了一下是因为这块儿对分析算法效率比较有用，而且高斯模糊的算法真的很漂亮~

 

金字塔多分辨率

金字塔是早期图像多尺度的表示形式。图像金字塔化一般包括两个步骤：使用低通滤波器平滑图像；对平滑图像进行降采样（通常是水平，竖直方向1/2），从而得到一系列尺寸缩小的图像。

上图中（a）是对原始信号进行低通滤波，（b）是降采样得到的信号。

而对于二维图像，一个传统的金字塔中，每一层图像由上一层分辨率的长、宽各一半，也就是四分之一的像素组成：

多尺度和多分辨率

尺度空间表达和金字塔多分辨率表达之间最大的不同是：

• 尺度空间表达是由不同高斯核平滑卷积得到，在所有尺度上有相同的分辨率；
• 而金字塔多分辨率表达每层分辨率减少固定比率。

所以，金字塔多分辨率生成较快，且占用存储空间少；而多尺度表达随着尺度参数的增加冗余信息也变多。

多尺度表达的优点在于图像的局部特征可以用简单的形式在不同尺度上描述；而金字塔表达没有理论基础，难以分析图像局部特征。

DoG（Difference of Gaussian）

高斯拉普拉斯LoG金字塔

结合尺度空间表达和金字塔多分辨率表达，就是在使用尺度空间时使用金字塔表示，也就是计算机视觉中最有名的拉普拉斯金子塔（ 《The Laplacian pyramid as a compact image code》）。

高斯拉普拉斯LoG（Laplace of Guassian）算子就是对高斯函数进行拉普拉斯变换：

核心思想还是高斯，这个不多叙述。

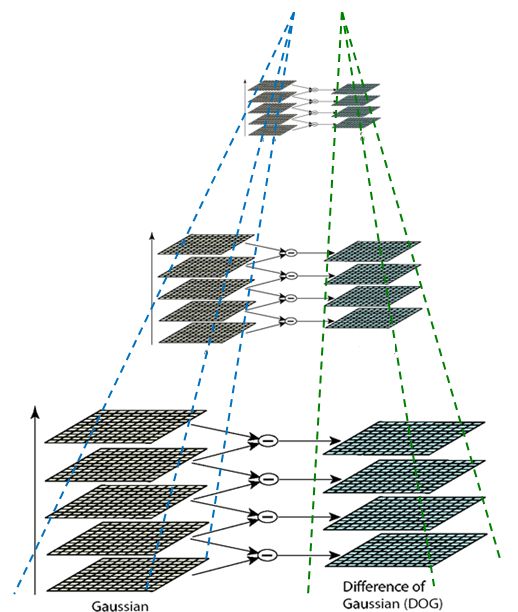
高斯差分DoG金字塔

DoG（Difference of Gaussian）其实是对高斯拉普拉斯LoG的近似，也就是对 的近似。SIFT算法建议，在某一尺度上的特征检测可以通过对两个相邻高斯尺度空间的图像相减，得到DoG的响应值图像D(x,y,σ)。然后仿照LoG方法，通过对响应值图像D(x,y,σ)进行局部最大值搜索，在空间位置和尺度空间定位局部特征点。其中：

k为相邻两个尺度空间倍数的常数。

上图中（a）是DoG的三维图，（b）是DoG与LoG的对比。

金字塔构建

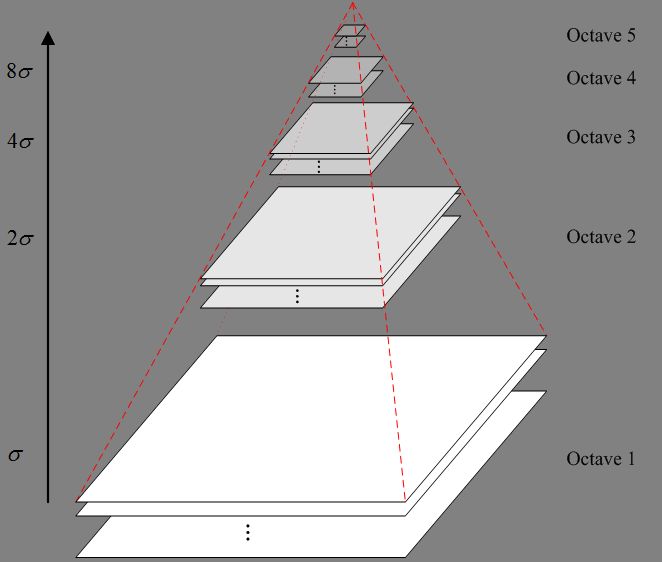
构建高斯金字塔

为了得到DoG图像，先要构造高斯金字塔。我们回过头来继续说高斯金字塔~

高斯金字塔在多分辨率金字塔简单 降采样基础上加了高斯滤波，也就是对金字塔每层图像用不同参数的σ做高斯模糊，使得每层金字塔有多张高斯模糊图像。金字塔每层多张图像合称为一组（Octave），每组有多张（也叫层Interval）图像。另外，降采样时，金字塔上边一组图像的第一张图像（最底层的一张）是由前一组（金字塔下面一组）图像的倒数第三张隔点采样得到。

以下是OpenCV中构建高斯金字塔的代码，我加了相应的注释：

// 构建nOctaves组（每组nOctaves+3层）高斯金字塔
void SIFT::buildGaussianPyramid( const Mat& base, vector<Mat>& pyr, int nOctaves ) const
{
    vector<double> sig(nOctaveLayers + 3);
    pyr.resize(nOctaves*(nOctaveLayers + 3));

    // precompute Gaussian sigmas using the following formula:
    //  \sigma_{total}^2 = \sigma_{i}^2 + \sigma_{i-1}^2、
	// 计算对图像做不同尺度高斯模糊的尺度因子
    sig[0] = sigma;
    double k = pow( 2., 1. / nOctaveLayers );
    for( int i = 1; i < nOctaveLayers + 3; i++ )
    {
        double sig_prev = pow(k, (double)(i-1))*sigma;
        double sig_total = sig_prev*k;
        sig[i] = std::sqrt(sig_total*sig_total - sig_prev*sig_prev);
    }

    for( int o = 0; o < nOctaves; o++ )
    {
		// DoG金子塔需要nOctaveLayers+2层图像来检测nOctaves层尺度
		// 所以高斯金字塔需要nOctaveLayers+3层图像得到nOctaveLayers+2层DoG金字塔
        for( int i = 0; i < nOctaveLayers + 3; i++ )
        {
			// dst为第o组（Octave）金字塔
            Mat& dst = pyr[o*(nOctaveLayers + 3) + i];
			// 第0组第0层为原始图像
            if( o == 0  &&  i == 0 )
                dst = base;
            
			// base of new octave is halved image from end of previous octave
			// 每一组第0副图像时上一组倒数第三幅图像隔点采样得到
            else if( i == 0 )
            {
                const Mat& src = pyr[(o-1)*(nOctaveLayers + 3) + nOctaveLayers];
                resize(src, dst, Size(src.cols/2, src.rows/2),
                       0, 0, INTER_NEAREST);
            }
			// 每一组第i副图像是由第i-1副图像进行sig[i]的高斯模糊得到
			// 也就是本组图像在sig[i]的尺度空间下的图像
            else
            {
                const Mat& src = pyr[o*(nOctaveLayers + 3) + i-1];
                GaussianBlur(src, dst, Size(), sig[i], sig[i]);
            }
        }
    }
}

高斯金字塔的组数为：

代码10-17行是计算高斯模糊的系数σ，具体关系如下：

其中，σ为尺度空间坐标，s为每组中层坐标，σ0为初始尺度，S为每组层数（一般为3~5）。根据这个公式，我们可以得到金字塔组内各层尺度以及组间各图像尺度关系。

组内相邻图像尺度关系：

相邻组间尺度关系：

所以， 相邻两组的同一层尺度为2倍的关系。

最终尺度序列总结为：

o为金字塔组数，n为每组金字塔层数。

构建DoG金字塔

构建高斯金字塔之后，就是用金字塔相邻图像相减构造DoG金字塔。

下面为构造DoG的代码：

// 构建nOctaves组（每组nOctaves+2层）高斯差分金字塔
void SIFT::buildDoGPyramid( const vector<Mat>& gpyr, vector<Mat>& dogpyr ) const
{
    int nOctaves = (int)gpyr.size()/(nOctaveLayers + 3);
    dogpyr.resize( nOctaves*(nOctaveLayers + 2) );

    for( int o = 0; o < nOctaves; o++ )
    {
        for( int i = 0; i < nOctaveLayers + 2; i++ )
        {
			// 第o组第i副图像为高斯金字塔中第o组第i+1和i组图像相减得到
            const Mat& src1 = gpyr[o*(nOctaveLayers + 3) + i];
            const Mat& src2 = gpyr[o*(nOctaveLayers + 3) + i + 1];
            Mat& dst = dogpyr[o*(nOctaveLayers + 2) + i];
            subtract(src2, src1, dst, noArray(), CV_16S);
        }
    }
}

这个比较简单，就是一个 subtract()函数。

至此，SIFT第一步就完成了。参见《SIFT原理与源码分析》

（转载请注明作者和出处：http://blog.csdn.net/xiaowei_cqu未经允许请勿用于商业用途）