重复数据删除(De-duplication)技术研究
1、Dedupe概述
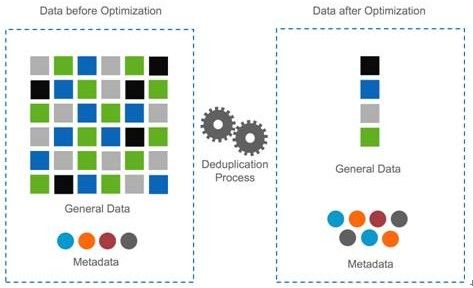
De-duplication,即重复数据删除,它是一种目前主流且非常热门的存储技术,可对存储容量进行有效优化。它通过删除数据集中重复的数 据,只保留其中一份,从而消除冗余数据。如下图所示。这种技术可以很大程度上减少对物理存储空间的需求,从而满足日益增长的数据存储需求。Dedupe技 术可以带许多实际的利益,主要包括以下诸多方面:
(1) 满足ROI(投资回报率,Return On Investment)/TCO(总持有成本,Total Cost of Ownership)需求;
(2) 可以有效控制数据的急剧增长;
(3) 增加有效存储空间,提高存储效率;
(4) 节省存储总成本和管理成本;
(5) 节省数据传输的网络带宽;
(6) 节省空间、电力供应、冷却等运维成本。
Dedupe技术目前大量应用于数据备份与归档系统,因为对数据进行多次备份后,存在大量重复数据,非常适合这种技术。事实上,dedupe技术 可以用于很多场合,包括在线数据、近线数据、离线数据存储系统,可以在文件系统、卷管理器、NAS、SAN中实施。Dedupe也可以用于数据容灾、数据 传输与同步,作为一种数据压缩技术可用于数据打包。Dedupe技术可以帮助众多应用降低数据存储量,节省网络带宽,提高存储效率、减小备份窗口,节省成 本。
Dedupe的衡量维度主要有两个,即重复数据删除率(deduplocation ratios)和性能。Dedupe性能取决于具体实现技术,而重复数据删除率则由数据自身的特征和应用模式所决定,影响因素如下表[2]所示。目前各存 储厂商公布的重复数据删除率从20:1到500:1不等。
| 高重复数据删除率 |
低重复数据删除率 |
| 数据由用户创建 |
数据从自然世界获取 |
| 数据低变化率 |
数据高变化率 |
| 引用数据、非活动数据 |
活动数据 |
| 低数据变化率应用 |
高数据变化率应用 |
| 完全数据备份 |
增量数据备份 |
| 数据长期保存 |
数据短期保存 |
| 大范围数据应用 |
小范围数据应用 |
| 持续数据业务处理 |
普通数据业务处理 |
| 小数据分块 |
大数据分块 |
| 变长数据分块 |
定长数据分块 |
| 数据内容可感知 |
数据内容不可知 |
| 时间数据消重 |
空间数据消重 |
2、Dedupe实现要点
研发或应用Dedupe技术时应该考虑各种因素,因为这些因素会直接影响其性能和效果。
(1) What:对何种数据进行消重?
对时间数据还是空间数据进行消重,对全局数据还是局部数据 进行消重?这是首先需要考虑的因素,这直接决定着Dedupe实现技术和数据消重率。随时间变化的数据,如周期性的备份、归档数据,比空间数据具有更高的 消重率,Dedupe技术在备份归档领域中被广泛应用。不难想象,全局范围内的数据重复率比局部范围数据要高,会获得更高的数据消重率。
(2) When:何时进行消重?
数据消重时机分为两种情形:在线消重和离线消重。采用在线消重模 式,数据写入存储系统同时执行消重,因此实际传输或写入的数据量较少,适合通过LAN或WAN进行数据处理的存储系统,如网络备份归档和异地容灾系统。由 于它需要实时进行文件切分、数据指纹计算、Hash查找,对系统资料消耗大。离线消重模式,先将数据写入存储系统,然后利用适当的时间再进行消重处理。这 种模式与前面一种刚好相反,它对系统资料消耗少,但写入了包含重复的数据,需要更多的额外存储空间来预先存储消重前数据。这种模式适合直连存储DAS和存 储区域网络SAN存储架构,数据传输不占用网络带宽。另外,离线消重模式需要保证有足够的时间窗口来进行数据去重操作。总之,在何时进行消重,要根据实际 存储应用场景来确定。
(3) Where:在何处进行消重?
数据消重可以在源端(Source)或者目标端 (Target)进行。源端消重在数据源进行,传输的是已经消重后的数据,能够节省网络带宽,但会占用大量源端系统资源。目标端消重发生在目标端,数据在 传输到目标端再进行消重,它不会占用源端系统资源,但占用大量网络带宽。目标端消重的优势在于它对应用程序透明,并具有良好的互操作性,不需要使用专门的 API,现有应用软件不用作任何修改即可直接应用。
(4) How:如何进行消重?
重复数据删除技术包含许多技术实现细节,包括文件如何进行切分?数 据块指纹如何计算?如何进行数据块检索?采用相同数据检测还是采用相似数据检测和差异编码技术?数据内容是否可以感知,是否需要对内容进行解析?这些都是 Dedupe具体实现息息相关。本文主要研究相同数据检测技术,基于二进制文件进行消重处理,具有更广泛的适用性。
3、Dedupe关键技术
存储系统的重复数据删除过程一般是这样的:首先将数据文件分割成一组数据块,为每个数据块计算指纹,然后以指纹为关键字进行Hash查找,匹配则 表示该数据块为重复数据块,仅存储数据块索引号,否则则表示该数据块是一个新的唯一块,对数据块进行存储并创建相关元信息。这样,一个物理文件在存储系统 就对应一个逻辑表示,由一组FP组成的元数据。当进行读取文件时,先读取逻辑文件,然后根据FP序列,从存储系统中取出相应数据块,还原物理文件副本。从 如上过程中可以看出,Dedupe的关键技术主要包括文件数据块切分、数据块指纹计算和数据块检索。
(1) 文件数据块切分
Dedupe按照消重的粒度可以分为文件级和数据块级。文件级的dedupe技术也称为单一实例存储(SIS, Single Instance Store),数据块级的重复数据删除其消重粒度更小,可以达到4-24KB之间。显然,数据块级的可以提供更高的数据消重率,因此目前主流的 dedupe产品都是数据块级的。数据分块算法主要有三种,即定长切分(fixed-size partition)、CDC切分(content-defined chunking)和滑动块(sliding block)切分。定长分块算法采用预先义好的块大小对文件进行切分,并进行弱校验值和md5强校验值。弱校验值主要是为了提升差异编码的性能,先计算弱 校验值并进行hash查找,如果发现则计算md5强校验值并作进一步hash查找。由于弱校验值计算量要比md5小很多,因此可以有效提高编码性能。定长 分块算法的优点是简单、性能高,但它对数据插入和删除非常敏感,处理十分低效,不能根据内容变化作调整和优化。Deduputil中FSP分块算法代码如 下。
- /*
- * fixed-sized file chunking
- */
- static int file_chunk_fsp( int fd, int fd_ldata, int fd_bdata, unsigned int *pos, unsigned int *block_num,
- block_id_t **metadata, hashtable *htable, char *last_block_buf, unsigned int *last_block_len)
- {
- int ret = 0;
- unsigned int rwsize;
- unsigned char md5_checksum[16 + 1] = {0};
- char *buf = NULL;
- buf = (char *)malloc(g_block_size);
- if (buf == NULL)
- {
- perror("malloc in file_chunk_fsp" );
- return errno;
- }
- while (rwsize = read(fd, buf, g_block_size))
- {
- /* if the last block */
- if (rwsize != g_block_size)
- break ;
- /* calculate md5 */
- md5(buf, rwsize, md5_checksum);
- if (0 != (ret = dedup_regfile_block_process(buf, rwsize, md5_checksum, fd_ldata,
- fd_bdata, pos, block_num, metadata, htable)))
- {
- perror("dedup_regfile_block_process in file_chunk_fsp" );
- goto _FILE_CHUNK_FSP_EXIT;
- }
- }
- *last_block_len = (rwsize > 0) ? rwsize : 0;
- if ((*last_block_len)) memcpy(last_block_buf, buf, *last_block_len);
- _FILE_CHUNK_FSP_EXIT:
- if (buf) free(buf);
- return ret;
- }
CDC(content-defined chunking)算法是一种变长分块算法,它应用数据指纹(如Rabin指纹)将文件分割成长度大小不等的分块策略。与定长分块算法不同,它是基于文件 内容进行数据块切分的,因此数据块大小是可变化的。算法执行过程中,CDC使用一个固定大小(如48字节)的滑动窗口对文件数据计算数据指纹。如果指纹满 足某个条件,如当它的值模特定的整数等于预先设定的数时,则把窗口位置作为块的边界。CDC算法可能会出现病态现象,即指纹条件不能满足,块边界不能确 定,导致数据块过大。实现中可以对数据块的大小进行限定,设定上下限,解决这种问题。CDC算法对文件内容变化不敏感,插入或删除数据只会影响到检少的数 据块,其余数据块不受影响。CDC算法也是有缺陷的,数据块大小的确定比较困难,粒度太细则开销太大,粒度过粗则dedup效果不佳。如何两者之间权衡折 衷,这是一个难点。Deduputil中CDC分块算法代码如下。
- /*
- * content-defined chunking:
- * 1. BLOCK_MIN_SIZE <= block_size <= BLOCK_MAX_SIZE
- * 2. hash(block) % d == r
- */
- static int file_chunk_cdc( int fd, int fd_ldata, int fd_bdata, unsigned int *pos, unsigned int *block_num,
- block_id_t **metadata, hashtable *htable, char *last_block_buf, unsigned int *last_block_len)
- {
- char buf[BUF_MAX_SIZE] = {0};
- char block_buf[BLOCK_MAX_SIZE] = {0};
- char win_buf[BLOCK_WIN_SIZE + 1] = {0};
- char adler_pre_char;
- unsigned char md5_checksum[16 + 1] = {0};
- unsigned int bpos = 0;
- unsigned int rwsize = 0;
- unsigned int exp_rwsize = BUF_MAX_SIZE;
- unsigned int head, tail;
- unsigned int block_sz = 0, old_block_sz = 0;
- unsigned int hkey = 0;
- int ret = 0;
- while (rwsize = read(fd, buf + bpos, exp_rwsize))
- {
- /* last chunk */
- if ((rwsize + bpos + block_sz) < BLOCK_MIN_SIZE)
- break ;
- head = 0;
- tail = bpos + rwsize;
- /* avoid unnecessary computation and comparsion */
- if (block_sz < (BLOCK_MIN_SIZE - BLOCK_WIN_SIZE))
- {
- old_block_sz = block_sz;
- block_sz = ((block_sz + tail - head) > (BLOCK_MIN_SIZE - BLOCK_WIN_SIZE)) ?
- BLOCK_MIN_SIZE - BLOCK_WIN_SIZE : block_sz + tail -head;
- memcpy(block_buf + old_block_sz, buf + head, block_sz - old_block_sz);
- head += (block_sz - old_block_sz);
- }
- while ((head + BLOCK_WIN_SIZE) <= tail)
- {
- memcpy(win_buf, buf + head, BLOCK_WIN_SIZE);
- /*
- * Firstly, i think rabinhash is the best. However, it's performance is very bad.
- * After some testing, i found ELF_hash is better both on performance and dedup rate.
- * So, EFL_hash is default. Now, adler_hash as default.
- */
- if (g_rolling_hash)
- {
- hkey = (block_sz == (BLOCK_MIN_SIZE - BLOCK_WIN_SIZE)) ? adler32_checksum(win_buf, BLOCK_WIN_SIZE) :
- adler32_rolling_checksum(hkey, BLOCK_WIN_SIZE, adler_pre_char, buf[head+BLOCK_WIN_SIZE-1]);
- }
- else
- hkey = g_cdc_chunk_hashfunc(win_buf);
- /* get a normal chunk */
- if ((hkey % g_block_size) == CHUNK_CDC_R)
- {
- memcpy(block_buf + block_sz, buf + head, BLOCK_WIN_SIZE);
- head += BLOCK_WIN_SIZE;
- block_sz += BLOCK_WIN_SIZE;
- if (block_sz >= BLOCK_MIN_SIZE)
- {
- md5(block_buf, block_sz, md5_checksum);
- if (0 != (ret = dedup_regfile_block_process(block_buf, block_sz,
- md5_checksum, fd_ldata, fd_bdata, pos, block_num, metadata, htable)))
- {
- perror("dedup_reggile_block_process in file_chunk_cdc" );
- goto _FILE_CHUNK_CDC_EXIT;
- }
- block_sz = 0;
- }
- }
- else
- {
- block_buf[block_sz++] = buf[head++];
- /* get an abnormal chunk */
- if (block_sz >= BLOCK_MAX_SIZE)
- {
- md5(block_buf, block_sz, md5_checksum);
- if (0 != (ret = dedup_regfile_block_process(block_buf, block_sz,
- md5_checksum, fd_ldata, fd_bdata, pos, block_num, metadata, htable)))
- {
- perror("dedup_reggile_block_process in file_chunk_cdc" );
- goto _FILE_CHUNK_CDC_EXIT;
- }
- block_sz = 0;
- }
- }
- /* avoid unnecessary computation and comparsion */
- if (block_sz == 0)
- {
- block_sz = ((tail - head) > (BLOCK_MIN_SIZE - BLOCK_WIN_SIZE)) ?
- BLOCK_MIN_SIZE - BLOCK_WIN_SIZE : tail - head;
- memcpy(block_buf, buf + head, block_sz);
- head = ((tail - head) > (BLOCK_MIN_SIZE - BLOCK_WIN_SIZE)) ?
- head + (BLOCK_MIN_SIZE - BLOCK_WIN_SIZE) : tail;
- }
- adler_pre_char = buf[head -1];
- }
- /* read expected data from file to full up buf */
- bpos = tail - head;
- exp_rwsize = BUF_MAX_SIZE - bpos;
- adler_pre_char = buf[head -1];
- memmove(buf, buf + head, bpos);
- }
- /* last chunk */
- *last_block_len = ((rwsize + bpos + block_sz) >= 0) ? rwsize + bpos + block_sz : 0;
- if (*last_block_len > 0)
- {
- memcpy(last_block_buf, block_buf, block_sz);
- memcpy(last_block_buf + block_sz, buf, rwsize + bpos);
- }
- _FILE_CHUNK_CDC_EXIT:
- return ret;
- }
滑动块(sliding block)算法结合了定长切分和CDC切分的优点,块大小固定。它对定长数据块先计算弱校验值,如果匹配则再计算md5强校验值,两者都匹配则认为是一 个数据块边界。该数据块前面的数据碎片也是一个数据块,它是不定长的。如果滑动窗口移过一个块大小的距离仍无法匹配,则也认定为一个数据块边界。滑动块算 法对插入和删除问题处理非常高效,并且能够检测到比CDC更多的冗余数据,它的不足是容易产生数据碎片。Deduputil中SB分块算法代码如下。
- /*
- * slideing block chunking, performance is a big issue due to too many hash lookup.
- */
- static int file_chunk_sb( int fd, int fd_ldata, int fd_bdata, unsigned int *pos, unsigned int *block_num,
- block_id_t **metadata, hashtable *htable, char *last_block_buf, unsigned int *last_block_len)
- {
- char buf[BUF_MAX_SIZE] = {0};
- char win_buf[BLOCK_MAX_SIZE + 1] = {0};
- char block_buf[BLOCK_MAX_SIZE] = {0};
- char adler_pre_char;
- unsigned char md5_checksum[16 + 1] = {0};
- unsigned char md5_checksum1[16 + 1] = {0};
- unsigned char crc_checksum[16] = {0};
- unsigned int bpos = 0;
- unsigned int slide_sz = 0;
- unsigned int rwsize = 0;
- unsigned int exp_rwsize = BUF_MAX_SIZE;
- unsigned int head, tail;
- unsigned int hkey = 0;
- unsigned int bflag = 0;
- int ret = 0;
- while (rwsize = read(fd, buf + bpos, exp_rwsize))
- {
- /* last chunk */
- if ((rwsize + bpos + slide_sz) < g_block_size)
- break ;
- head = 0;
- tail = bpos + rwsize;
- while ((head + g_block_size) <= tail)
- {
- memcpy(win_buf, buf + head, g_block_size);
- hkey = (slide_sz == 0) ? adler32_checksum(win_buf, g_block_size) :
- adler32_rolling_checksum(hkey, g_block_size, adler_pre_char, buf[head+g_block_size-1]);
- uint_2_str(hkey, crc_checksum);
- bflag = 0;
- /* this block maybe is duplicate */
- if (hash_exist(g_sb_htable_crc, crc_checksum))
- {
- bflag = 2;
- md5(win_buf, g_block_size, md5_checksum);
- if (hash_exist(htable, md5_checksum))
- {
- /* insert fragment */
- if (slide_sz != 0)
- {
- md5(block_buf, slide_sz, md5_checksum1);
- if (0 != (ret = dedup_regfile_block_process(block_buf, slide_sz, md5_checksum1,
- fd_ldata, fd_bdata, pos, block_num, metadata, htable)))
- {
- perror("dedup_regfile_block_process in file_chunk_sb" );
- goto _FILE_CHUNK_SB_EXIT;
- }
- }
- /* insert fixed-size block */
- if (0 != (ret = dedup_regfile_block_process(win_buf, g_block_size, md5_checksum,
- fd_ldata, fd_bdata, pos, block_num, metadata, htable)))
- {
- perror("dedup_regfile_block_process in file_chunk_sb" );
- goto _FILE_CHUNK_SB_EXIT;
- }
- head += g_block_size;
- slide_sz = 0;
- bflag = 1;
- }
- }
- /* this block is not duplicate */
- if (bflag != 1)
- {
- block_buf[slide_sz] = buf[head];
- head++;
- slide_sz++;
- if (slide_sz == g_block_size)
- {
- if (bflag != 2) md5(block_buf, g_block_size, md5_checksum);
- if (0 != (ret = dedup_regfile_block_process(block_buf, g_block_size, md5_checksum,
- fd_ldata, fd_bdata, pos, block_num, metadata, htable)))
- {
- perror("dedup_regfile_block_process in file_chunk_sb" );
- goto _FILE_CHUNK_SB_EXIT;
- }
- hash_checkin(g_sb_htable_crc, crc_checksum);
- slide_sz = 0;
- }
- }
- adler_pre_char = buf[head - 1];
- }
- /* read expected data from file to full up buf */
- bpos = tail - head;
- exp_rwsize = BUF_MAX_SIZE - bpos;
- adler_pre_char = buf[head - 1];
- memmove(buf, buf + head, bpos);
- }
- /* last chunk */
- *last_block_len = ((rwsize + bpos + slide_sz) > 0) ? rwsize + bpos + slide_sz : 0;
- if (*last_block_len > 0)
- {
- memcpy(last_block_buf, block_buf, slide_sz);
- memcpy(last_block_buf + slide_sz, buf, rwsize + bpos);
- }
- _FILE_CHUNK_SB_EXIT:
- lseek(fd, 0, SEEK_SET);
- return ret;
- }
(2) 数据块指纹计算
数据指纹是数据块的本质特征,理想状态是每个唯一数据块具有唯一的数据指纹,不同的数据块具有不同的数据指纹。数据块本身往往较大,因此数据指纹 的目标是期望以较小的数据表示(如16、32、64、128字节)来区别不同数据块。数据指纹通常是对数据块内容进行相关数学运算获得,从当前研究成果来 看Hash函数比较接近与理想目标,比如MD5、SHA1、SHA-256、SHA-512、为one-Way、RabinHash等。另外,还有许多字符串Hash函数 也 可以用来计算数据块指纹。然而,遗憾的是这些指纹函数都存在碰撞问题,即不同数据块可能会产生相同的数据指纹。相对来说,MD5和SHA系列HASH函数 具有非常低的碰撞发生概率,因此通常被采用作为指纹计算方法。其中,MD5和SHA1是128位的,SHA-X(X表示位数)具有更低的碰撞发生概率,但 同时计算量也会大大增加。实际应用中,需要在性能和数据安全性方面作权衡。另外,还可以同时使用多种Hash算法来为数据块计算指纹。
(3) 数据块检索
对于大存储容量的Dedupe系统来说,数据块数量非常庞大,尤其是数据块粒度细的情况下。因此,在这样一个大的数据指纹库中检索,性能就会成为 瓶颈。信息检索方法有很多种,如动态数组、数据库、RB/B/B+/B*树、Hashtable等。Hash查找因为其O(1)的查找性能而著称,被对查 找性能要求高的应用所广泛采用,Dedupe技术中也采用它。Hashtable处于内存中,会消耗大量内存资源,在设计Dedupe前需要对内存需求作 合理规划。根据数据块指纹长度、数据块数量(可以由存储容量和平均数据块大小估算)可以估算出内存需求量。
散列表(Hashtable,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记 录的数组叫做散列表。散列表的查找过程基本上和造表过程相同,一些关键码可通过散列函数转换的地址直接找到,另一些关键码在散列函数得到的地址上产生了冲 突,需要按处理冲突的方法进行查找。详细请参考散列表设计 。
4、Dedupe数据安全
这里的数据安全包含两个层面的含义:一是数据块碰撞,二是数据可用性。这两种安全性对用户来说都是至关重要的,必须事先考虑。
数据块指纹FP(FingerPrinter)通常使用Hash函数来计算获得,如MD5、SHA1、SHA-256、SHA-512等。从纯数 学角度看,如果两个数据块指纹不同,则这两个数据块肯定不同。然而,如果两个数据块指纹相同,我们则不能断定这两个数据块是相同的。因为Hash函数会产 生碰撞,山东大学的王小云教授所带领的团队已经找到快速产生碰撞的方法。但是,这种碰撞的概率是非常非常小的,小到甚至低于磁盘发生损坏的概率,因此通常 近似认为:如果数据块指纹相同,则数据块相同。由于数据产生碰撞可能性的存在,Dedupe技术很少被用于关键数据存储的应用场合,一旦发生碰撞将产生巨 大的经济损失。针对这种问题,目前主要有两种解决路径:一是对数据指纹相同的块进行字节级完全比较,它的难点在于数据块原始数据有时难以方便获得,另外性 能会产生一定损失。本人开发的开源软件deduputil采用就是这种策略,详见deduputil数据块零碰撞算法 。二是最大可能降低碰撞产生的概率,即采用更优的Hash函数(如SHA-512, SHA-1024),或者采用两种以上hash算法组合方式,这显然会对性能造成影响。本人在"数据同步算法研究 "中采用的是该种方法,为每个数据块计算两个指纹,一个类似Rsync算法中的弱校验值(Rsync滚动校验算法 )和一个强校验值MD5。弱校验值计算消耗远小于MD5计算量,先计算目标数据块的弱校验值,如果与源数据块不同则不必再计算其MD5校验值,相同则计算MD5并作比较。这种方式以较小的性能代价极大地降低了碰撞产生的概率,而且通过优化,性能损失无几。
Dedupe仅保存唯一的数据副本,如果该副本发生损坏将造成所有相关数据文件不可访问,数据可用性压力要高于不作Dedupe许多。数据可用性 问题可以采用传统数据保护方法来解决,常用的方式包括数据冗余(RAID1,RAID5, RAID6)、本地备份与复制、远程备份与复制、纠错数据编码技术(如海明码、信息分散算法IDA)、分布式存储技术。这些技术均可以有效消除单点故障, 从而提高数据可用性。当然,这需要付出一定代价,以空