Consistent hashing
Consistent hashing算法
网站为了支撑更大的用户访问量,往往需要对用户访问的数据做cache,对于访问量特别大的门户网站,一般都提供专门的cache服务机群和负载均衡来专 门处理缓存,负载均衡的算法很多,轮循算法、哈希算法、最少连接算法、响应速度算法等,hash算法是比较常用的一种,它的常用思想是先计算出一个 hash值,然后使用 CRC余数算法将hash值和机器数mod后取余数,机器的编号可以是0到N-1(N是机器数),计算出的结果一一对应即可。我们知道缓存最关键的就是命中率这个因素,如果命中率非常低,那么缓存也就失去了它的意义,因此实际生产环境中我们的一个重要目标就是提高缓存命中率。如 上所述,采用一般的CRC取余的hash算法虽然能达到负载均衡的目的,但是它存在一个严重的问题,那就是如果我们其中一台服务器down掉,那么我们就 需要在计算缓存过程中将这台服务器去掉,即N台服务器,目前就只有N-1台提供缓存服务,此时需要一个rehash过程,而reash得到的结果将导致正 常的用户请求不能找到原来缓存数据的正确机器,其他N-1台服务器上的缓存数据将大量失效,此时所有的用户请求全部会集中到数据库上,严重可能导致整个生 产环境挂掉.
举个例子,有5台服务器,他们编号分别是0(A),1(B),2(C),3(D),4(E) ,正常情况下,假设用户数据hash值为12,那么对应的数据应该缓存在12%5=2号服务器上,假设编号为3的服务器此时挂掉,那么将其移除后就得到一 个新的0(A),1(B),2(C),3(E)(注:这里的编号3其实就是原来的4号服务器)服务器列表,此时用户来取数据,同样hash值为 12,rehash后的得到的机器编号12%4=0号服务器,可见,此时用户到0号服务器去找数据明显就找不到,出现了cache不命中现象,如果不命中 此时应用会从后台数据库重新读取数据再cache到0号服务器上,如果大量用户出现这种情况,那么后果不堪设想。同样,增加一台缓存服务器,也会导致同样 的后果,感兴趣的读者可以自行推敲。
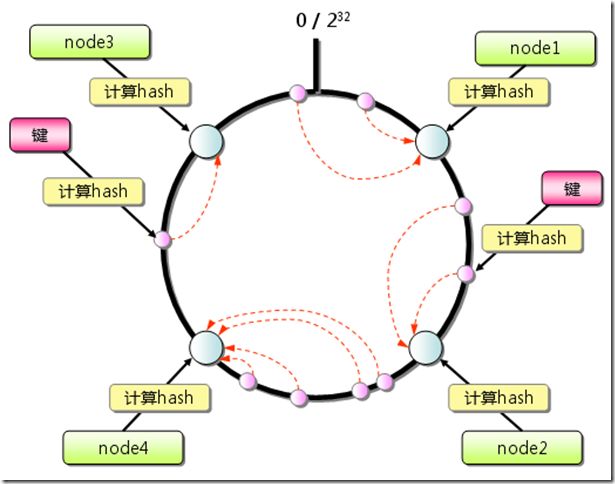
可以有一种设想,要提高命中率就得减少增加或者移除服务器rehash带来的影响,那么有这样一种算法么?Consistent hashing算法就是这样一种hash算法,它的算法思想是:首先求出服务器(节点)的哈希值,并将其配置到0~2^32的圆上。然后用同样的方法求出 存储数据的键的哈希值,并映射到圆上。然后从数据映射到的位置开始顺时针查找,将数据保存到找到的第一个服务器上。如果超过2^32仍然找不到服务器,就 会保存到第一台服务器上。下面有一张比较经典的图,直接用过来,不修改了。
图一 Consistent Hashing原理示意图
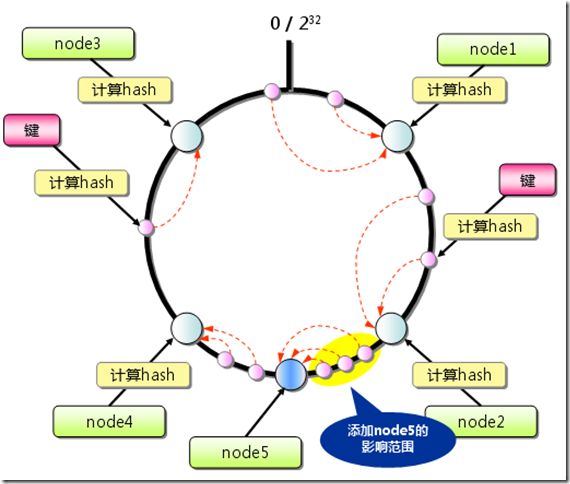
这里有四台服务器,我们假设增加一台服务器Node5,可以看到,它影响的数据只是在增加Node5逆时针方向的数据会受到影响。同样,删除其中一台服务器,例如删除服务器node4,那么影响的数据也只是node4上缓存的数据。
图二 Consistent Hashing添加服务器
Consistent Hashing最大限度地抑制了hash键的重新分布。另外要取得比较好的负载均衡的效果,往往在服务器数量比较少的时候需要增加虚拟节点来保证服务器能 均匀的分布在圆环上。因为使用一般的hash方法,服务器的映射地点的分布非常不均匀。使用虚拟节点的思想,为每个物理节点(服务器)在圆上分配 100~200个点。这样就能抑制分布不均匀,最大限度地减小服务器增减时的缓存重新分布。用户数据映射在虚拟节点上,就表示用户数据真正存储位置是在该 虚拟节点代表的实际物理服务器上。
下面有一个图描述了需要为每台物理服务器增加的虚拟节点。
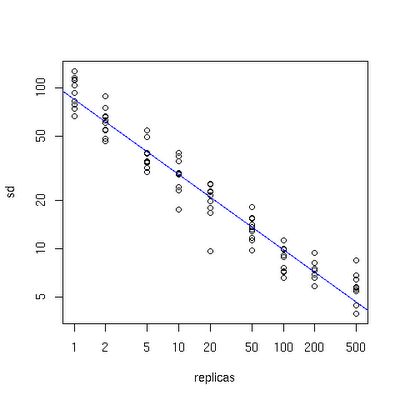
图三 虚拟节点倍数- 物理节点数关系图
x轴表示的是需要为每台物理服务器扩展的虚拟节点倍数(scale),y轴是实际物理服务器数,可以看出,当物理服务器的数量很小时,需要更大的虚拟节 点,反之则需要更少的节点,从图上可以看出,在物理服务器有10台时,差不多需要为每台服务器增加100~200个虚拟节点才能达到真正的负载均衡。
下面是一个简单的java参考实现:
import java.util.Collection;
import java.util.SortedMap;
import java.util.TreeMap;
public class ConsistentHash<T> {
private final HashFunction hashFunction;
private final int numberOfReplicas;
private final SortedMap<Integer, T> circle = new TreeMap<Integer, T>();
public ConsistentHash(
HashFunction hashFunction, //hash算法
int numberOfReplicas,//虚拟节点数
Collection<T> nodes//物理节点
) {
this.hashFunction = hashFunction;
this.numberOfReplicas = numberOfReplicas;
for (T node : nodes) {
add(node);
}
}
public void add(T node) {
for (int i = 0; i < numberOfReplicas; i++) {
circle.put(hashFunction.hash(node.toString() + i), node);
}
}
public void remove(T node) {
for (int i = 0; i < numberOfReplicas; i++) {
circle.remove(hashFunction.hash(node.toString() + i));
}
}
//关键算法
public T get(Object key) {
if (circle.isEmpty()) {
return null;
}
int hash = hashFunction.hash(key);
if (!circle.containsKey(hash)) {
SortedMap<Integer, T> tailMap = circle.tailMap(hash);
hash = tailMap.isEmpty() ? circle.firstKey() : tailMap.firstKey();
}
return circle.get(hash);
}
}
本文转自
http://blog.csdn.net/lovingprince/archive/2009/10/09/4645448.aspx
3q
原文作者。