Neil Brown精妙的avl实现
最近在复习数据结构,看到avl树,这样比较复杂的数据结构通常都很搞人。于是上网,找到一个实现看,写这代码的老外叫Neil Brown,一个大胡子,我们知道,在国外,开发人员的水平经常和胡子的多少成正比。还看到他在blog中说,这个代码打算用在linux kernel里,自然不会是普通代码了。
我拿下来,狠看一阵才看懂,不得不说,这个代码很多地方的实现是很精妙的,和教材上只是为了让你理解概念的代码,区别很大。
这个实现有一个特点,就是没有一般树实现中的left和right指针,作者用一个数组next[2]来表示,next[0]就是左子树,next[1]就是右子树,然后每个节点也不保存当前的层高,这个是教科书的做法,int longer:2,极其省俭的表示了是左子树长(值为0),还是右子树长(值为1),或者当前节点上这颗树是平衡的(值了-1)。
这里开始精妙了,我们平时的tree查找是怎么写的,target小于当前节点就下到左子树
继续找,大于就下到右子树继续找,这里就用一个direction next_step = (target > tree->value)得到了接下来操作的方向。next[next_step]就是接下来要查找的节点
作者不大喜欢single rotation和double rotation这样的说法,他把旋转分为两种,一种是2旋,就是single rotation,这个时候用数组的优势就出来了,不用把相似的single rotation写两遍,传入的dir值不同就可以了。
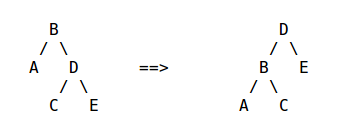
这里是三旋转,也就是double rotation.
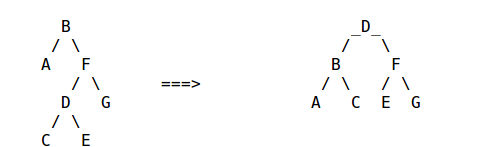
注意旋转后面third变量的作用,third表示新入节点在C还是在E上。如果在E上,独立的C的高度必小于A,因为在E上还没有插入新节点时,C只比A高1,而且C上有D,F垫底,所以独立的C的高度要减2,所以独立的C比独立的A高度小1。
插入新节点后已经,树已经不平衡了,需要重新计算节点上的longer值。
这里是插入新节点后使树重新平衡的全过程,包括旋转节点和更新高度信息。path_top是更新的起点。如果path_top节点是平衡的,不需要旋转,更新高度信息即可。如果在较短和路径上插入,也不需要旋转,还是更新高度信息,path_top变成平衡的,然后对插入的那棵树更新高度信息。如果在较长的路径上插入,就需要旋转了,first和second表示两次的操作方向,如果相同,就是2旋转,否则是3旋转,这时要注意third变量,如果C和E都为空,那么third变量就是NEITHER,不需要特殊处理,否则,third就传入3旋转的函数,用于下面更新高度信息。
avl_insert是插入接口,这里又有一个技巧,对于avl树,不用从根节点上开始更新高度信息。开始更新高度信息的起点,是path_top。如果查找的一路上下来,每个节点都是平衡的,那么只能从根上开始更新,否则,从第一个不平衡的节点开始更新。插入完成后,再调用avl_rebalance_insert来平衡树。
明天再写删除的,太晚了。
我拿下来,狠看一阵才看懂,不得不说,这个代码很多地方的实现是很精妙的,和教材上只是为了让你理解概念的代码,区别很大。
这个实现有一个特点,就是没有一般树实现中的left和right指针,作者用一个数组next[2]来表示,next[0]就是左子树,next[1]就是右子树,然后每个节点也不保存当前的层高,这个是教科书的做法,int longer:2,极其省俭的表示了是左子树长(值为0),还是右子树长(值为1),或者当前节点上这颗树是平衡的(值了-1)。
/*
* Usage: avl3 list of integers ...
*
* Each integer will be checked to see if it is currently in
* the AVL tree. If not, it will be inserted. If so, it will
* be deleted. The tree starts out empty and the final tree is
* printed (on its side) in an ASCII-art style
*/
#include <stdlib.h>
typedef int value_t;
#define LEFT 0 // 表示左节点,或者左子树长
#define RIGHT 1 // 表示右节点,或者右子树长
#define NEITHER -1 // 以当前节点为根的子树是平衡的
typedef int direction; //重定向一个,表示操作是在左子树还是右子树上
// 树节点的定义
typedef struct node_s {
value_t value;
struct node_s *next[2];
int longer:2;
} *node;
#define Balanced(n) (n->longer < 0) // 平衡时值了-1
这里开始精妙了,我们平时的tree查找是怎么写的,target小于当前节点就下到左子树
继续找,大于就下到右子树继续找,这里就用一个direction next_step = (target > tree->value)得到了接下来操作的方向。next[next_step]就是接下来要查找的节点
node avl_find(node tree, value_t target)
{
while (tree && target != tree->value) {
direction next_step = (target > tree->value);
tree = tree->next[next_step];
}
return tree;
}
作者不大喜欢single rotation和double rotation这样的说法,他把旋转分为两种,一种是2旋,就是single rotation,这个时候用数组的优势就出来了,不用把相似的single rotation写两遍,传入的dir值不同就可以了。
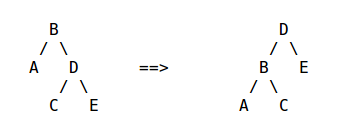
static node avl_rotate_2(node *path_top, direction dir)
{
node B, C, D, E;
B = *path_top;
D = B->next[dir];
C = D->next[1-dir];
E = D->next[dir];
*path_top = D;
D->next[1-dir] = B;
B->next[dir] = C;
B->longer = NEITHER;
D->longer = NEITHER;
return E;
}
这里是三旋转,也就是double rotation.
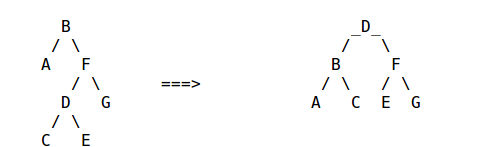
注意旋转后面third变量的作用,third表示新入节点在C还是在E上。如果在E上,独立的C的高度必小于A,因为在E上还没有插入新节点时,C只比A高1,而且C上有D,F垫底,所以独立的C的高度要减2,所以独立的C比独立的A高度小1。
static node avl_rotate_3(node *path_top, direction dir, direction third)
{
node B, F, D, C, E;
B = *path_top;
F = B->next[dir];
D = F->next[1-dir];
/* note: C and E can be NULL */
C = D->next[1-dir];
E = D->next[dir];
*path_top = D;
D->next[1-dir] = B;
D->next[dir] = F;
B->next[dir] = C;
F->next[1-dir] = E;
D->longer = NEITHER;
/* assume both trees are balanced */
B->longer = F->longer = NEITHER;
if (third == NEITHER)
return NULL;
else if (third == dir) {
/* E holds the insertion so B is unbalanced */
B->longer = 1-dir;
return E;
} else {
/* C holds the insertion so F is unbalanced */
F->longer = dir;
return C;
}
}
插入新节点后已经,树已经不平衡了,需要重新计算节点上的longer值。
/***************************************************
* INSERTION *
***************************************************/
static inline void avl_rebalance_path(node path, value_t target)
{
/* Each node in path is currently balanced.
* Until we find target, mark each node as longer
* in the direction of target because we know we have
* inserted target there
*/
while (path && target != path->value) {
direction next_step = (target > path->value);
path->longer = next_step;
path = path->next[next_step];
}
}
这里是插入新节点后使树重新平衡的全过程,包括旋转节点和更新高度信息。path_top是更新的起点。如果path_top节点是平衡的,不需要旋转,更新高度信息即可。如果在较短和路径上插入,也不需要旋转,还是更新高度信息,path_top变成平衡的,然后对插入的那棵树更新高度信息。如果在较长的路径上插入,就需要旋转了,first和second表示两次的操作方向,如果相同,就是2旋转,否则是3旋转,这时要注意third变量,如果C和E都为空,那么third变量就是NEITHER,不需要特殊处理,否则,third就传入3旋转的函数,用于下面更新高度信息。
static inline void avl_rebalance_insert(node *path_top, value_t target)
{
node path = *path_top;
direction first, second, third;
if (Balanced(path))
;
else if (path->longer != (first = (target > path->value))) {
/* took the shorter path */
path->longer = NEITHER;
path = path->next[first];
} else if (first == (second = (target > path->next[first]->value))) {
/* just a two-point rotate */
path = avl_rotate_2(path_top, first);
} else {
/* fine details of the 3 point rotate depend on the third step.
* However there may not be a third step, if the third point of the
* rotation is the newly inserted point. In that case we record
* the third step as NEITHER
*/
path = path->next[first]->next[second];
if (target == path->value) third = NEITHER;
else third = (target > path->value);
path = avl_rotate_3(path_top, first, third);
}
avl_rebalance_path(path, target);
}
avl_insert是插入接口,这里又有一个技巧,对于avl树,不用从根节点上开始更新高度信息。开始更新高度信息的起点,是path_top。如果查找的一路上下来,每个节点都是平衡的,那么只能从根上开始更新,否则,从第一个不平衡的节点开始更新。插入完成后,再调用avl_rebalance_insert来平衡树。
int avl_insert(node *treep, value_t target)
{
/* insert the target into the tree, returning 1 on success or 0 if it
* already existed
*/
node tree = *treep;
node *path_top = treep;
while (tree && target != tree->value) {
direction next_step = (target > tree->value);
if (!Balanced(tree)) path_top = treep;
treep = &tree->next[next_step];
tree = *treep;
}
if (tree) return 0;
tree = malloc(sizeof(*tree));
tree->next[0] = tree->next[1] = NULL;
tree->longer = NEITHER;
tree->value = target;
*treep = tree;
avl_rebalance_insert(path_top, target);
return 1;
}
明天再写删除的,太晚了。