彻底弄懂最大堆的四种操作(图解+程序)（JAVA）

http://128kj.iteye.com/blog/1728555

堆有最大堆和最小堆之分，最大堆就是每个节点的值都>=其左右孩子（如果有的话）值的完全二叉树。最小堆便是每个节点的值都<=其左右孩子值的完全二叉树。 

  设有n个元素的序列{k1,k2,...,kn},当且仅当满足下列关系时,称之为堆。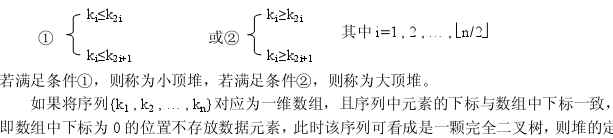 
 

堆的三种基本操作(以下以最大堆为例)： 
⑴最大堆的插入   

    由于需要维持完全二叉树的形态，需要先将要插入的结点x放在最底层的最右边，插入后满 足完全二叉树的特点； 
  然后把x依次向上调整到合适位置满足堆的性质,例如下图中插入80,先将80放在最后,然后两次上浮到合适位置. 
  时间：O(logn)。  “结点上浮”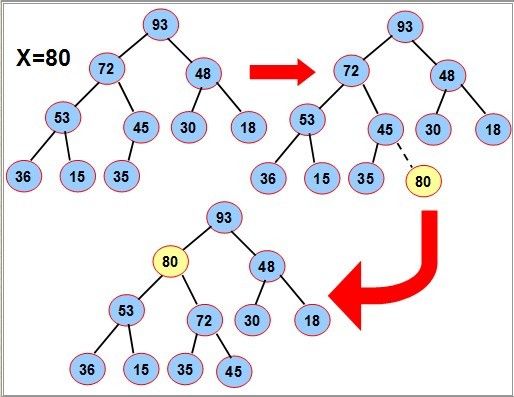 
 

程序实现: 

//向最大堆中插入元素, heap:存放堆元素的数组
   public static void insert(List<Integer> heap, int value) {
      //在数组的尾部添加
       if(heap.size()==0)
         heap.add(0);//数组下标为0的位置不放元素
       heap.add(value);
       //开始上升操作
      // heapUp2(heap, heap.size() - 1);
       heapUp(heap, heap.size() - 1);

   }

   //上升，让插入的数和父节点的数值比较，当大于父节点的时候就和父节点的值相交换
   public static void heapUp(List<Integer> heap, int index) {

       //注意由于数值是从下标为1开始，当index = 1的时候，已经是根节点了
       if (index > 1) {
           //求出父亲的节点
           int parent = index / 2;

           //获取相应位置的数值
           int parentValue = (Integer) heap.get(parent);
           int indexValue = (Integer) heap.get(index);
           //如果父亲节点比index的数值小，就交换二者的数值
           if (parentValue < indexValue) {
               //交换数值
               swap(heap, parent, index);
               //递归调用
               heapUp(heap, parent);
           }

       }
   }

⑵删除 
   操作原理是：当删除节点的数值时，原来的位置就会出现一个孔,填充这个孔的方法就是， 
把最后的叶子的值赋给该孔并下调到合适位置，最后把该叶子删除。 
  
如图中要删除72,先用堆中最后一个元素来35替换72,再将35下沉到合适位置,最后将叶子节点删除。 
　　“结点下沉”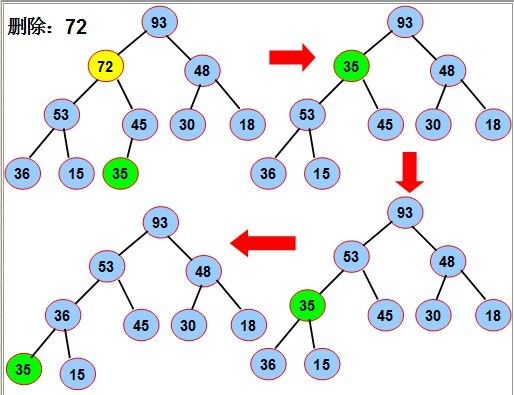 

 

程序:
 /**
     * 删除堆中位置是index处的节点
     * 操作原理是：当删除节点的数值时，原来的位置就会出现一个孔
     * 填充这个孔的方法就是，把最后的叶子的值赋给该孔，最后把该叶子删除
     * @param heap
     */
    public static void delete(List<Integer> heap,int index) {
        //把最后的一个叶子的数值赋值给index位置
        heap.set(index, heap.get(heap.size() - 1));
        //下沉操作
        //heapDown2(heap, index);
        heapDown(heap, index);
        //把最后一个位置的数字删除
        heap.remove(heap.size() - 1);
    }


    /**
     * 递归实现
     * 删除堆中一个数据的时候，根据堆的性质，应该把相应的位置下移，才能保持住堆性质不变
     * @param heap 保持堆元素的数组
     * @param index 被删除的那个节点的位置
     */
    public static void heapDown(List<Integer> heap, int index) {
        //因为第一个位置存储的是空值，不在考虑之内
        int n = heap.size() - 2;

        //记录最大的那个儿子节点的位置
        int child = -1;

        //2*index>n说明该节点没有左右儿子节点了，那么就返回
        if (2 * index > n) {
            return;
        } //如果左右儿子都存在
        else if (2 * index < n) {

            //定义左儿子节点
            child = 2 * index;
            //如果左儿子小于右儿子的数值，取右儿子的下标
            if ((Integer) heap.get(child) < (Integer) heap.get(child + 1)) {
                child++;
            }

        }//如果只有一个儿子（左儿子节点）
        else if (2 * index == n) {
            child = 2 * index;
        }

        if ((Integer) heap.get(child) > (Integer) heap.get(index)) {
            //交换堆中的child，和index位置的值
            swap(heap, child, index);

            //完成交换后递归调用，继续下降
            heapDown(heap, child);
        }
    }

⑶初始化 
方法1：插入法： 
  从空堆开始，依次插入每一个结点，直到所有的结点全部插入到堆为止。 
  时间：O(n*log(n)) 
  方法2：调整法： 
    序列对应一个完全二叉树；从最后一个分支结点（n div 2）开始，到根（1）为止，依次对每个分支结点进行调整（下沉），以便形成以每个分支结点为根的堆，当最后对树根结点进行调整后，整个树就变成了一个堆。 
  时间：O(n) 
对如图的序列,要使其成为堆,我们从最后一个分支结点(10/2),其值为72开始,依次对每个分支节点53,18,36 45进行调整(下沉).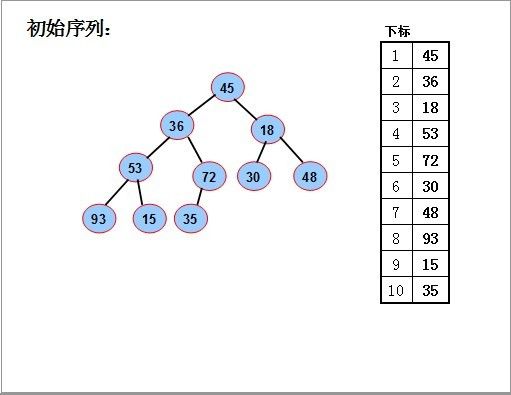 
 
 
 

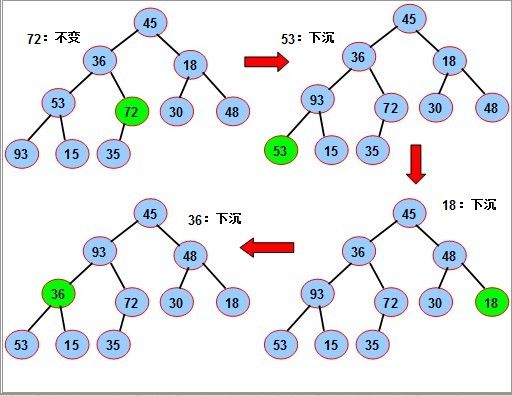
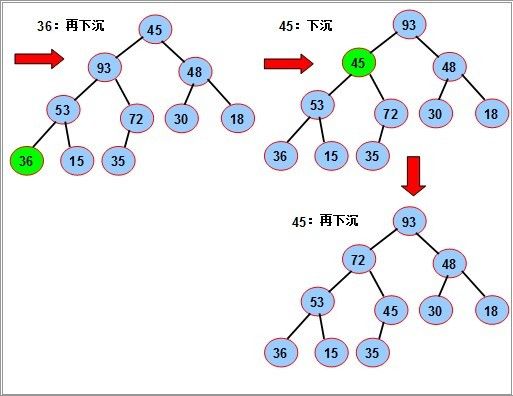
程序:

     /*根据树的性质建堆，树节点前一半一定是分支节点，即有孩子的，所以我们从这里开始调整出初始堆*/
     public static void adjust(List<Integer> heap){
        for (int i = heap.size() / 2; i > 0; i--)
            adjust(heap,i, heap.size()-1);


        System.out.println("=================================================");
        System.out.println("调整后的初始堆：");
          print(heap);
      }

    /**
     * 调整堆，使其满足堆得定义
     * @param i
     * @param n
     */
    public static void adjust(List<Integer> heap,int i, int n) {

        int child;
        for (; i <= n / 2; ) {
            child = i * 2;
            if(child+1<=n&&heap.get(child)<heap.get(child+1))
                child+=1;/*使child指向值较大的孩子*/
            if(heap.get(i)< heap.get(child)){
                swap(heap,i, child);
                /*交换后，以child为根的子树不一定满足堆定义，所以从child处开始调整*/
                i = child;

            }  else break;
        }
    }

(4)最大堆排序  

//对一个最大堆heap排序
   public static void heapSort(List<Integer> heap) {

       for (int i = heap.size()-1; i > 0; i--) {
        /*把根节点跟最后一个元素交换位置，调整剩下的n-1个节点，即可排好序*/
           swap(heap,1, i);
           adjust(heap,1, i - 1);
       }
   }

(5)完整的代码 

import java.util.*;

/**
 *实现的最大堆的插入和删除操作
 * @author Arthur
 */
public class Heap {

     /**
     * 删除堆中位置是index处的值
     * 操作原理是：当删除节点的数值时，原来的位置就会出现一个孔
     * 填充这个孔的方法就是，把最后的叶子的值赋给该孔，最后把该叶子删除
     * @param heap 一个最大堆
     */
    public static void delete(List<Integer> heap,int index) {
        //把最后的一个叶子的数值赋值给index位置
        heap.set(index, heap.get(heap.size() - 1));
        //下沉操作
        //heapDown2(heap, index);
        heapDown(heap, index); //节点下沉
        //把最后一个位置的数字删除
        heap.remove(heap.size() - 1);
    }


    /**
     * 节点下沉递归实现
     * 删除一个堆中一个数据的时候，根据堆的性质，应该把相应的位置下移，才能保持住堆性质不变
     * @param heap 保持最大堆元素的数组
     * @param index 被删除的那个节点的位置
     */
    public static void heapDown(List<Integer> heap, int index) {
        //因为第一个位置存储的是空值，不在考虑之内
        int n = heap.size() - 2;

        //记录最大的那个儿子节点的位置
        int child = -1;

        //2*index>n说明该节点没有左右儿子节点了，那么就返回
        if (2 * index > n) {
            return;
        } //如果左右儿子都存在
        else if (2 * index < n) {

            //定义左儿子节点
            child = 2 * index;
            //如果左儿子小于右儿子的数值，取右儿子的下标
            if ((Integer) heap.get(child) < (Integer) heap.get(child + 1)) {
                child++;
            }

        }//如果只有一个儿子（左儿子节点）
        else if (2 * index == n) {
            child = 2 * index;
        }

        if ((Integer) heap.get(child) > (Integer) heap.get(index)) {
            //交换堆中的child，和index位置的值
            swap(heap, child, index);

            //完成交换后递归调用，继续下降
            heapDown(heap, child);
        }
    }

    //非递归实现
    public static void heapDown2(List<Integer> heap, int index) {
        int child = 0;//存储左儿子的位置

        int temp = (Integer) heap.get(index);
        int n = heap.size() - 2;
        //如果有儿子的话
        for (; 2 * index <= n; index = child) {
            //获取左儿子的位置
            child = 2 * index;
            //如果只有左儿子
            if (child == n) {
                child = 2 * index;
            } //如果右儿子比左儿子的数值大
            else if ((Integer) heap.get(child) < (Integer) heap.get(child + 1)) {
                child++;
            }

            //如果数值最大的儿子比temp的值大
            if ((Integer) heap.get(child) >temp) {
                //交换堆中的child，和index位置的值
                swap(heap, child, index);
            } else {
                break;
            }
        }
    }


     //打印链表
    public static void print(List<Integer> list) {
        for (int i = 1; i < list.size(); i++) {
            System.out.print(list.get(i) + " ");
        }
        System.out.println();
    }

    //把堆中的a,b位置的值互换
    public static void swap(List<Integer> heap, int a, int b) {
        //临时存储child位置的值
        int temp = (Integer) heap.get(a);

        //把index的值赋给child的位置
        heap.set(a, heap.get(b));

        //把原来的child位置的数值赋值给index位置
        heap.set(b, temp);
    }

    //向最大堆中插入元素
    public static void insert(List<Integer> heap, int value) {
           //在数组的尾部添加要插入的元素
        if(heap.size()==0)
          heap.add(0);//数组下标为0的位置不放元素
        heap.add(value);
        //开始上升操作
       // heapUp2(heap, heap.size() - 1);
        heapUp(heap, heap.size() - 1);

    }

    //节点上浮，让插入的数和父节点的数值比较，当大于父节点的时候就和节点的值相交换
    public static void heapUp(List<Integer> heap, int index) {

        //注意由于数值是从小标为一开始，当index = 1的时候，已经是根节点了
        if (index > 1) {
            //保存父亲的节点
            int parent = index / 2;

            //获取相应位置的数值
            int parentValue = (Integer) heap.get(parent);
            int indexValue = (Integer) heap.get(index);
            //如果父亲节点比index的数值小，就交换二者的数值
            if (parentValue < indexValue) {
                //交换数值
                swap(heap, parent, index);
                //递归调用
                heapUp(heap, parent);
            }

        }
    }

    //非递归实现
    public static void heapUp2(List<Integer> heap, int index) {
        int parent = 0;
        for (; index > 1; index /= 2) {
            //获取index的父节点的下标
            parent = index / 2;

            //获得父节点的值
            int parentValue = (Integer) heap.get(parent);
            //获得index位置的值
            int indexValue = (Integer) heap.get(index);

            //如果小于就交换
            if (parentValue < indexValue) {
                swap(heap, parent, index);
            }
        }
    }

     /*根据树的性质建堆，树节点前一半一定是分支节点，即有孩子的，所以我们从这里开始调整出初始堆*/
     public static void adjust(List<Integer> heap){
        for (int i = heap.size() / 2; i > 0; i--)
            adjust(heap,i, heap.size()-1);


        System.out.println("=================================================");
        System.out.println("调整后的初始堆：");
          print(heap);
      }

    /**
     * 调整堆，使其满足堆得定义
     * @param i
     * @param n
     */
    public static void adjust(List<Integer> heap,int i, int n) {

        int child;
        for (; i <= n / 2; ) {
            child = i * 2;
            if(child+1<=n&&heap.get(child)<heap.get(child+1))
                child+=1;/*使child指向值较大的孩子*/
            if(heap.get(i)< heap.get(child)){
                swap(heap,i, child);
                /*交换后，以child为根的子树不一定满足堆定义，所以从child处开始调整*/
                i = child;

            }  else break;
        }
    }

   //对一个最大堆heap排序
    public static void heapSort(List<Integer> heap) {

        for (int i = heap.size()-1; i > 0; i--) {
        /*把根节点跟最后一个元素交换位置，调整剩下的n-1个节点，即可排好序*/
            swap(heap,1, i);
            adjust(heap,1, i - 1);
        }
    }

   public static void main(String args[]) {
        List<Integer> array = new ArrayList<Integer>(Arrays.asList(null, 1, 2, 5, 10, 3, 7, 11, 15, 17, 20, 9, 15, 8, 16));
        adjust(array);//调整使array成为最大堆

        delete(array,8);//堆中删除下标是8的元素
        System.out.println("删除后");
        print(array);

        insert(array, 99);//堆中插入
        print(array);

        heapSort(array);//排序
        System.out.println("将堆排序后:");
        print(array);
        System.out.println("-------------------------");
        List<Integer> array1=new ArrayList<Integer>();
        insert(array1,0);
        insert(array1, 1);insert(array1, 2);insert(array1, 5);
        insert(array1, 10);insert(array1, 3);insert(array1, 7);
        insert(array1, 11);insert(array1, 15); insert(array1, 17);
        insert(array1, 20);insert(array1, 9);
        insert(array1, 15);insert(array1, 8);insert(array1, 16);
        print(array1);

        System.out.println("==============================");
        array=new ArrayList<Integer>(Arrays.asList(null,45,36,18,53,72,30,48,93,15,35));
        adjust(array);
          insert(array, 80);//堆中插入
          print(array);
         delete(array,2);//堆中删除80的元素
         print(array);
         delete(array,2);//堆中删除72的元素
         print(array);

    }
}

程序运行: 
D:\java>java   Heap 
================================================= 
调整后的初始堆： 
20 17 16 15 9 15 11 1 10 3 2 7 8 5 
删除后 
20 17 16 15 9 15 11 5 10 3 2 7 8 
99 17 20 15 9 15 16 5 10 3 2 7 8 11 
将堆排序后: 
2 3 5 7 8 9 10 11 15 15 16 17 20 99 
------------------------- 
20 17 16 10 15 9 15 0 5 2 11 1 7 3 8 
============================== 
================================================= 
调整后的初始堆： 
93 72 48 53 45 30 18 36 15 35 
93 80 48 53 72 30 18 36 15 35 45 
93 72 48 53 45 30 18 36 15 35 
93 53 48 36 45 30 18 35 15 
源码下载