Reward
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2791 Accepted Submission(s): 819
The workers will compare their rewards ,and some one may have demands of the distributing of rewards ,just like a's reward should more than b's.Dandelion's unclue wants to fulfill all the demands, of course ,he wants to use the least money.Every work's reward will be at least 888 , because it's a lucky number.
then m lines ,each line contains two integers a and b ,stands for a's reward should be more than b's.
题意:
有n(1到10000)个人与m(1到20000)个关系,每个关系都有两个数a和b,表示a的钱数必须大于b的钱数,即a>b,根据所给出的关系来输出总共所需分配的钱数最少,每人最低分配钱数为888,如果给出的关系条件无论如何都无法达到则输出-1。
思路:
拓扑排序,判断是否有环和一共有多少层,有环说明不满足关系条件,输出-1。有多少层的意思就是,一个人可以同时大于几个人的钱数,那么这几个人的钱数相同,要使钱数最少,那么这几个人的钱数比那一个人的钱数多1块即为最少。用拓扑排序的话,就是每循环一次所有的顶点,算出有多少个入度为0的点,然后这几个顶点的钱数是相同的,将这几个点删去并且将这个顶点出发所到达终点的入度-1。有环即某一次循环会出现没有入度为0的情况,一旦出现这种情况就跳出整个循环,输出-1。
AC:
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define MAX 20000+5
//一开始WA了几次,发现是数组开小了
int main()
{
int u[MAX],v[MAX],fir[MAX],next[MAX];
int ind[MAX];
int n,m,time,temp,q,p;
__int64 sum,price;
//这里的钱数要用64位整型来存,要根据范围判断!
while(~scanf("%d%d",&n,&m))
{
memset(ind,0,sizeof(ind));
memset(fir,-1,sizeof(fir));
//输入部分
for(int i=0;i<m;i++)
{
scanf("%d%d",&v[i],&u[i]);
next[i]=fir[u[i]];
fir[u[i]]=i;
ind[v[i]]++;
}
// printf("\ndegree:\n");
// for(int i=1;i<=n;i++)
// printf("%d ",ind[i]);
// printf("\n");
// system("pause");
//测试用
price=888;
sum=0;
temp=1;
q=1;
//q代表每次删去的顶点的标记是不一样的
//为什么要不一样?
while(1)
{
time=0;
p=0;
//p是为了判断当前状态是否已经全部判断完
for(int i=1;i<=n;i++)
if(ind[i]<0) p++;
//如果入度数组全部变为负数
//说明所有点都已经被删去
//这时候p应该等于n
for(int i=1;i<=n;i++)
if(!ind[i])
{
time++;
ind[i]=-q;
}
//判断有多少个入度为0的顶点
//如果判断出来该顶点入度为0,则次数+1且删去该点
// printf("\ndegree:\n");
// for(int i=1;i<=n;i++)
// printf("%d ",ind[i]);
// printf("\n");
// system("pause");
if(!time&&p!=n) {temp=0;break;}
//判断在还未完全删去顶点之前,是否出现过全部顶点入度都不为0的情况
//即判断是否为环
if(p==n) break;
//p等于n的时候,说明已经全部点都已经删去
//这时候可以跳出循环了
else
{
sum+=(time*price);
//计算钱数
price++;
//这一层已经计算完毕,单价+1
for(int k=1;k<=n;k++)
{
if(ind[k]==-q)
{
for(int x=fir[k];x!=-1;x=next[x])
ind[v[x]]--;
}
}
//对这一层的顶点所到达终点入度-1处理
}
q++;
//q改变,作为标记下一层入度为0的顶点值
// printf("\ndegree:\n");
// for(int i=1;i<=n;i++)
// printf("%d ",ind[i]);
// printf("\n");
// system("pause");
}
if(!temp) printf("-1\n");
else printf("%I64d\n",sum);
}
return 0;
}
q的标记:
比如当输入的值为:
6 6
2 1
3 1
4 2
5 2
5 3
6 3
可以判断出,1在第一层,2和3在第二层,4,5和6在第三层。
如果每一次循环标记这一层入度都为一个固定的值-1的话,那么入度数组标记情况为:
第二次循环表示终点入度-1;
第三次循环表示删去第二层入度为0的顶点;
第四次循环本应该是对第二层顶点所到达终点入度-1的,但是因为第一层的也被标记成了-1,所以会先把第一层所达到终点的入度-1,这样的话,第二层被标记成了-2了,不再是-1了,那么第二层顶点所到达终点入度无法进行-1处理;
循环最后一次后,因为找不到入度为0的点,而且全部的数又没有变成负数,说明全部点还没被删去,那么说明有环,所以最终输出了-1这个值了。
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
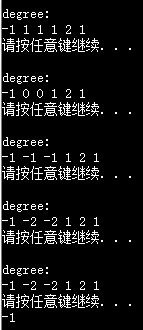
所以正确标记不同层的顶点的方法应该用不同的标记,故设了个变量p值,如图:
错误最后出错比较多是在开的数组开太小了,而且sum没有用64位整型,细节方面忽略了。