为什么选择跳表
目前经常使用的平衡数据结构有:B树,红黑树,AVL树,Splay Tree, Treep等。
想象一下,给你一张草稿纸,一只笔,一个编辑器,你能立即实现一颗红黑树,或者AVL树
出来吗? 很难吧,这需要时间,要考虑很多细节,要参考一堆算法与数据结构之类的树,
还要参考网上的代码,相当麻烦。
用跳表吧,跳表是一种随机化的数据结构,目前开源软件 Redis 和 LevelDB 都有用到它,
它的效率和红黑树以及 AVL 树不相上下,但跳表的原理相当简单,只要你能熟练操作链表,
就能轻松实现一个 SkipList。
有序表的搜索
考虑一个有序表:
从该有序表中搜索元素 < 23, 43, 59 > ,需要比较的次数分别为 < 2, 4, 6 >,总共比较的次数
为 2 + 4 + 6 = 12 次。有没有优化的算法吗? 链表是有序的,但不能使用二分查找。类似二叉
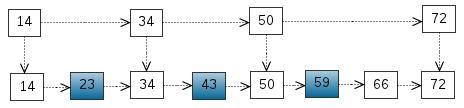
搜索树,我们把一些节点提取出来,作为索引。得到如下结构:
这里我们把 < 14, 34, 50, 72 > 提取出来作为一级索引,这样搜索的时候就可以减少比较次数了。
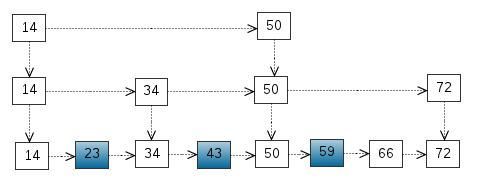
我们还可以再从一级索引提取一些元素出来,作为二级索引,变成如下结构:
这里元素不多,体现不出优势,如果元素足够多,这种索引结构就能体现出优势来了。
跳表
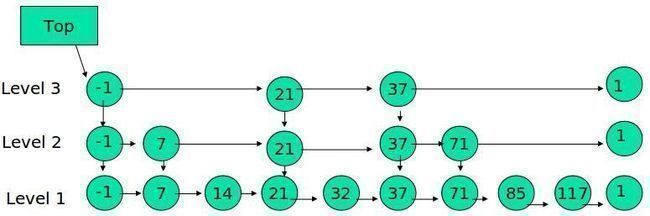
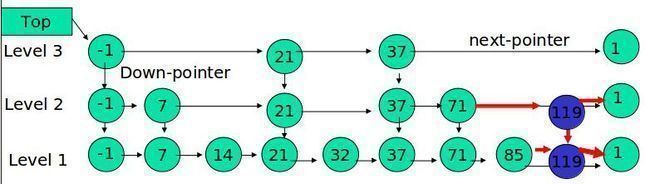
下面的结构是就是跳表:
其中 -1 表示 INT_MIN, 链表的最小值,1 表示 INT_MAX,链表的最大值。
跳表具有如下性质:
(1) 由很多层结构组成
(2) 每一层都是一个有序的链表
(3) 最底层(Level 1)的链表包含所有元素
(4) 如果一个元素出现在 Level i 的链表中,则它在 Level i 之下的链表也都会出现。
(5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
跳表的搜索
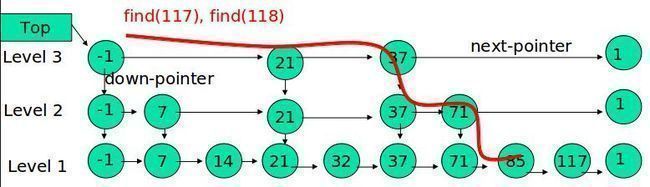
例子:查找元素 117
(1) 比较 21, 比 21 大,往后面找
(2) 比较 37, 比 37大,比链表最大值小,从 37 的下面一层开始找
(3) 比较 71, 比 71 大,比链表最大值小,从 71 的下面一层开始找
(4) 比较 85, 比 85 大,从后面找
(5) 比较 117, 等于 117, 找到了节点。
具体的搜索算法如下:
- /*如果存在x,返回x所在的节点,
- *否则返回x的后继节点*/
- find(x)
- {
- p=top;
- while(1){
- while(p->next->key<x)
- p=p->next;
- if(p->down==NULL)
- returnp->next;
- p=p->down;
- }
- }
跳表的插入
先确定该元素要占据的层数 K(采用丢硬币的方式,这完全是随机的)
然后在 Level 1 ... Level K 各个层的链表都插入元素。
例子:插入 119, K = 2
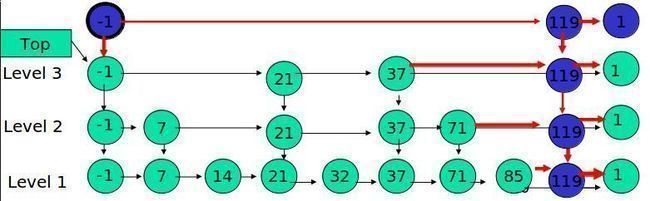
如果 K 大于链表的层数,则要添加新的层。
例子:插入 119, K = 4
丢硬币决定 K
插入元素的时候,元素所占有的层数完全是随机的,通过一下随机算法产生:
- intrandom_level()
- {
- K=1;
- while(random(0,1))
- K++;
- returnK;
- }
相当与做一次丢硬币的实验,如果遇到正面,继续丢,遇到反面,则停止,
用实验中丢硬币的次数 K 作为元素占有的层数。显然随机变量 K 满足参数为 p = 1/2 的几何分布,
K 的期望值 E[K] = 1/p = 2. 就是说,各个元素的层数,期望值是 2 层。
跳表的高度。
n 个元素的跳表,每个元素插入的时候都要做一次实验,用来决定元素占据的层数 K,
跳表的高度等于这n 次实验中产生的最大 K,待续。。。
跳表的空间复杂度分析
根据上面的分析,每个元素的期望高度为 2, 一个大小为 n 的跳表,其节点数目的
期望值是 2n。
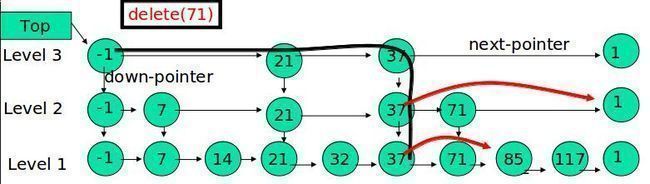
跳表的删除
在各个层中找到包含 x 的节点,使用标准的 delete from list 方法删除该节点。
例子:删除 71
- #include<stdio.h>
- #include<stdlib.h>
- #include<malloc.h>
- typedefintkey_t;
- typedefintvalue_t;
- typedefstructnode_t
- {
- key_tkey;
- value_tvalue;
- structnode_t*forward[];
- }node_t;
- typedefstructskiplist
- {
- intlevel;
- intlength;
- node_t*header;
- }list_t;
- #defineMAX_LEVEL16
- #defineSKIPLIST_P0.25
- node_t*slCreateNode(intlevel,key_tkey,value_tvalue)
- {
- node_t*n=(node_t*)malloc(sizeof(node_t)+level*sizeof(node_t*));
- if(n==NULL)returnNULL;
- n->key=key;
- n->value=value;
- returnn;
- }
- list_t*slCreate(void)
- {
- list_t*l=(list_t*)malloc(sizeof(list_t));
- inti=0;
- if(l==NULL)returnNULL;
- l->length=0;
- l->level=0;
- l->header=slCreateNode(MAX_LEVEL-1,0,0);
- for(i=0;i<MAX_LEVEL;i++)
- {
- l->header->forward[i]=NULL;
- }
- returnl;
- }
- intrandomLevel(void)
- {
- intlevel=1;
- while((rand()&0xFFFF)<(SKIPLIST_P*0xFFFF))
- level+=1;
- return(level<MAX_LEVEL)?level:MAX_LEVEL;
- }
- value_t*slSearch(list_t*list,key_tkey)
- {
- node_t*p=list->header;
- inti;
- for(i=list->level-1;i>=0;i--)
- {
- while(p->forward[i]&&(p->forward[i]->key<=key)){
- if(p->forward[i]->key==key){
- return&p->forward[i]->value;
- }
- p=p->forward[i];
- }
- }
- returnNULL;
- }
- intslDelete(list_t*list,key_tkey)
- {
- node_t*update[MAX_LEVEL];
- node_t*p=list->header;
- node_t*last=NULL;
- inti=0;
- for(i=list->level-1;i>=0;i--){
- while((last=p->forward[i])&&(last->key<key)){
- p=last;
- }
- update[i]=p;
- }
- if(last&&last->key==key){
- for(i=0;i<list->level;i++){
- if(update[i]->forward[i]==last){
- update[i]->forward[i]=last->forward[i];
- }
- }
- free(last);
- for(i=list->level-1;i>=0;i--){
- if(list->header->forward[i]==NULL){
- list->level--;
- }
- }
- list->length--;
- }else{
- return-1;
- }
- return0;
- }
- intslInsert(list_t*list,key_tkey,value_tvalue)
- {
- node_t*update[MAX_LEVEL];
- node_t*p,*node=NULL;
- intlevel,i;
- p=list->header;
- for(i=list->level-1;i>=0;i--){
- while((node=p->forward[i])&&(node->key<key)){
- p=node;
- }
- update[i]=p;
- }
- if(node&&node->key==key){
- node->value=value;
- return0;
- }
- level=randomLevel();
- if(level>list->level)
- {
- for(i=list->level;i<level;i++){
- update[i]=list->header;
- }
- list->level=level;
- }
- node=slCreateNode(level,key,value);
- for(i=0;i<level;i++){
- node->forward[i]=update[i]->forward[i];
- update[i]->forward[i]=node;
- }
- list->length++;
- return0;
- }
- intmain(intargc,char**argv)
- {
- list_t*list=slCreate();
- node_t*p=NULL;
- value_t*val=NULL;
- //插入
- for(inti=1;i<=15;i++){
- slInsert(list,i,i*10);
- }
- //删除
- if(slDelete(list,12)==-1){
- printf("delete:notfound\n");
- }else{
- printf("delete:deletesuccess\n");
- }
- //查找
- val=slSearch(list,1);
- if(val==NULL){
- printf("search:notfound\n");
- }else{
- printf("search:%d\n",*val);
- }
- //遍历
- p=list->header->forward[0];
- for(inti=0;i<list->length;i++){
- printf("%d,%d\n",p->key,p->value);
- p=p->forward[0];
- }
- getchar();
- return0;
- }
http://www.cxphp.com/?p=234(Redis中c语言的实现)
http://imtinx.iteye.com/blog/1291165
http://kenby.iteye.com/blog/1187303
http://bbs.bccn.net/thread-228556-1-1.html
http://blog.csdn.net/xuqianghit/article/details/6948554(leveldb源码)
- 上一篇:文件锁定flock结构
为什么选择跳表
目前经常使用的平衡数据结构有:B树,红黑树,AVL树,Splay Tree, Treep等。
想象一下,给你一张草稿纸,一只笔,一个编辑器,你能立即实现一颗红黑树,或者AVL树
出来吗? 很难吧,这需要时间,要考虑很多细节,要参考一堆算法与数据结构之类的树,
还要参考网上的代码,相当麻烦。
用跳表吧,跳表是一种随机化的数据结构,目前开源软件 Redis 和 LevelDB 都有用到它,
它的效率和红黑树以及 AVL 树不相上下,但跳表的原理相当简单,只要你能熟练操作链表,
就能轻松实现一个 SkipList。
有序表的搜索
考虑一个有序表:
从该有序表中搜索元素 < 23, 43, 59 > ,需要比较的次数分别为 < 2, 4, 6 >,总共比较的次数
为 2 + 4 + 6 = 12 次。有没有优化的算法吗? 链表是有序的,但不能使用二分查找。类似二叉
搜索树,我们把一些节点提取出来,作为索引。得到如下结构:
这里我们把 < 14, 34, 50, 72 > 提取出来作为一级索引,这样搜索的时候就可以减少比较次数了。
我们还可以再从一级索引提取一些元素出来,作为二级索引,变成如下结构:
这里元素不多,体现不出优势,如果元素足够多,这种索引结构就能体现出优势来了。
跳表
下面的结构是就是跳表:
其中 -1 表示 INT_MIN, 链表的最小值,1 表示 INT_MAX,链表的最大值。
跳表具有如下性质:
(1) 由很多层结构组成
(2) 每一层都是一个有序的链表
(3) 最底层(Level 1)的链表包含所有元素
(4) 如果一个元素出现在 Level i 的链表中,则它在 Level i 之下的链表也都会出现。
(5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
跳表的搜索
例子:查找元素 117
(1) 比较 21, 比 21 大,往后面找
(2) 比较 37, 比 37大,比链表最大值小,从 37 的下面一层开始找
(3) 比较 71, 比 71 大,比链表最大值小,从 71 的下面一层开始找
(4) 比较 85, 比 85 大,从后面找
(5) 比较 117, 等于 117, 找到了节点。
具体的搜索算法如下:
- /*如果存在x,返回x所在的节点,
- *否则返回x的后继节点*/
- find(x)
- {
- p=top;
- while(1){
- while(p->next->key<x)
- p=p->next;
- if(p->down==NULL)
- returnp->next;
- p=p->down;
- }
- }
跳表的插入
先确定该元素要占据的层数 K(采用丢硬币的方式,这完全是随机的)
然后在 Level 1 ... Level K 各个层的链表都插入元素。
例子:插入 119, K = 2
如果 K 大于链表的层数,则要添加新的层。
例子:插入 119, K = 4
丢硬币决定 K
插入元素的时候,元素所占有的层数完全是随机的,通过一下随机算法产生:
- intrandom_level()
- {
- K=1;
- while(random(0,1))
- K++;
- returnK;
- }
相当与做一次丢硬币的实验,如果遇到正面,继续丢,遇到反面,则停止,
用实验中丢硬币的次数 K 作为元素占有的层数。显然随机变量 K 满足参数为 p = 1/2 的几何分布,
K 的期望值 E[K] = 1/p = 2. 就是说,各个元素的层数,期望值是 2 层。
跳表的高度。
n 个元素的跳表,每个元素插入的时候都要做一次实验,用来决定元素占据的层数 K,
跳表的高度等于这n 次实验中产生的最大 K,待续。。。
跳表的空间复杂度分析
根据上面的分析,每个元素的期望高度为 2, 一个大小为 n 的跳表,其节点数目的
期望值是 2n。
跳表的删除
在各个层中找到包含 x 的节点,使用标准的 delete from list 方法删除该节点。
例子:删除 71
- #include<stdio.h>
- #include<stdlib.h>
- #include<malloc.h>
- typedefintkey_t;
- typedefintvalue_t;
- typedefstructnode_t
- {
- key_tkey;
- value_tvalue;
- structnode_t*forward[];
- }node_t;
- typedefstructskiplist
- {
- intlevel;
- intlength;
- node_t*header;
- }list_t;
- #defineMAX_LEVEL16
- #defineSKIPLIST_P0.25
- node_t*slCreateNode(intlevel,key_tkey,value_tvalue)
- {
- node_t*n=(node_t*)malloc(sizeof(node_t)+level*sizeof(node_t*));
- if(n==NULL)returnNULL;
- n->key=key;
- n->value=value;
- returnn;
- }
- list_t*slCreate(void)
- {
- list_t*l=(list_t*)malloc(sizeof(list_t));
- inti=0;
- if(l==NULL)returnNULL;
- l->length=0;
- l->level=0;
- l->header=slCreateNode(MAX_LEVEL-1,0,0);
- for(i=0;i<MAX_LEVEL;i++)
- {
- l->header->forward[i]=NULL;
- }
- returnl;
- }
- intrandomLevel(void)
- {
- intlevel=1;
- while((rand()&0xFFFF)<(SKIPLIST_P*0xFFFF))
- level+=1;
- return(level<MAX_LEVEL)?level:MAX_LEVEL;
- }
- value_t*slSearch(list_t*list,key_tkey)
- {
- node_t*p=list->header;
- inti;
- for(i=list->level-1;i>=0;i--)
- {
- while(p->forward[i]&&(p->forward[i]->key<=key)){
- if(p->forward[i]->key==key){
- return&p->forward[i]->value;
- }
- p=p->forward[i];
- }
- }
- returnNULL;
- }
- intslDelete(list_t*list,key_tkey)
- {
- node_t*update[MAX_LEVEL];
- node_t*p=list->header;
- node_t*last=NULL;
- inti=0;
- for(i=list->level-1;i>=0;i--){
- while((last=p->forward[i])&&(last->key<key)){
- p=last;
- }
- update[i]=p;
- }
- if(last&&last->key==key){
- for(i=0;i<list->level;i++){
- if(update[i]->forward[i]==last){
- update[i]->forward[i]=last->forward[i];
- }
- }
- free(last);
- for(i=list->level-1;i>=0;i--){
- if(list->header->forward[i]==NULL){
- list->level--;
- }
- }
- list->length--;
- }else{
- return-1;
- }
- return0;
- }
- intslInsert(list_t*list,key_tkey,value_tvalue)
- {
- node_t*update[MAX_LEVEL];
- node_t*p,*node=NULL;
- intlevel,i;
- p=list->header;
- for(i=list->level-1;i>=0;i--){
- while((node=p->forward[i])&&(node->key<key)){
- p=node;
- }
- update[i]=p;
- }
- if(node&&node->key==key){
- node->value=value;
- return0;
- }
- level=randomLevel();
- if(level>list->level)
- {
- for(i=list->level;i<level;i++){
- update[i]=list->header;
- }
- list->level=level;
- }
- node=slCreateNode(level,key,value);
- for(i=0;i<level;i++){
- node->forward[i]=update[i]->forward[i];
- update[i]->forward[i]=node;
- }
- list->length++;
- return0;
- }
- intmain(intargc,char**argv)
- {
- list_t*list=slCreate();
- node_t*p=NULL;
- value_t*val=NULL;
- //插入
- for(inti=1;i<=15;i++){
- slInsert(list,i,i*10);
- }
- //删除
- if(slDelete(list,12)==-1){
- printf("delete:notfound\n");
- }else{
- printf("delete:deletesuccess\n");
- }
- //查找
- val=slSearch(list,1);
- if(val==NULL){
- printf("search:notfound\n");
- }else{
- printf("search:%d\n",*val);
- }
- //遍历
- p=list->header->forward[0];
- for(inti=0;i<list->length;i++){
- printf("%d,%d\n",p->key,p->value);
- p=p->forward[0];
- }
- getchar();
- return0;
- }
http://www.cxphp.com/?p=234(Redis中c语言的实现)
http://imtinx.iteye.com/blog/1291165
http://kenby.iteye.com/blog/1187303
http://bbs.bccn.net/thread-228556-1-1.html
http://blog.csdn.net/xuqianghit/article/details/6948554(leveldb源码)