Sorting Slides（二分图最大匹配 + 匈牙利算法）

Sorting Slides

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 3110		Accepted: 1203

Description

Professor Clumsey is going to give an important talk this afternoon. Unfortunately, he is not a very tidy person and has put all his transparencies on one big heap. Before giving the talk, he has to sort the slides. Being a kind of minimalist, he wants to do this with the minimum amount of work possible. 

The situation is like this. The slides all have numbers written on them according to their order in the talk. Since the slides lie on each other and are transparent, one cannot see on which slide each number is written. 

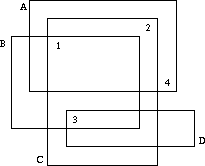
Well, one cannot see on which slide a number is written, but one may deduce which numbers are written on which slides. If we label the slides which characters A, B, C, ... as in the figure above, it is obvious that D has number 3, B has number 1, C number 2 and A number 4. 

Your task, should you choose to accept it, is to write a program that automates this process.

Input

The input consists of several heap descriptions. Each heap descriptions starts with a line containing a single integer n, the number of slides in the heap. The following n lines contain four integers xmin, xmax, ymin and ymax, each, the bounding coordinates of the slides. The slides will be labeled as A, B, C, ... in the order of the input. 

This is followed by n lines containing two integers each, the x- and y-coordinates of the n numbers printed on the slides. The first coordinate pair will be for number 1, the next pair for 2, etc. No number will lie on a slide boundary. 

The input is terminated by a heap description starting with n = 0, which should not be processed. 

Output

For each heap description in the input first output its number. Then print a series of all the slides whose numbers can be uniquely determined from the input. Order the pairs by their letter identifier. 

If no matchings can be determined from the input, just print the word none on a line by itself. 

Output a blank line after each test case. 

Sample Input

4
6 22 10 20
4 18 6 16
8 20 2 18
10 24 4 8
9 15
19 17
11 7
21 11
2
0 2 0 2
0 2 0 2
1 1
1 1
0

Sample Output

Heap 1
(A,4) (B,1) (C,2) (D,3)

Heap 2
none

 

       题意：

       给出N，后给出 N 个区域，每个区域给出Xi，Xj，Yi，Yj，说明这个区域是Xi ~ Xj，Yi ~ Yj 区域的。后给出 N 个点，给出每个点的 X ，Y 坐标。每个坐标都对应有一个区域，问能不能确定某些点在某个区域中。每个区域开始到结束用A,B,C,D,……来表示，点用1,2,3,4,……来表示。能确定则输出对应关系。若任何点都不能确定则输出none。

 

       思路：

       二分图最大匹配。这题与之前的题不同，找的是二分图必须边。并且要明确题意。

       每个点都会对应一个区域，相同的每个区域都会对应到一个值，所以这是满射的关系。现在要判断的是能不能确定下来每个点对应的是哪个区域。比如1号点对应的是A,B区域，2号点对应的也是A和B区域，那么就不能确定下来到底是1号点对应A区域还是2号点对应A区域了。

       既然是满射的话，任何区域或者点的度数为1的点，该边就应该是确定的边了，换句话说就是二分图最大匹配不能缺少的一条边，若缺少了的话，最大匹配就会减少了。继续往下看，当找完这条边后，删除这条边，那么与该边相关联的度为2点，也会产生一条必须边，递推下去的话，就是不断找必须边的过程，那么要找的就是二分图的必须边了。既然是必须边的话，缺少的话，最大匹配就会减少。

       而且，在这题还有隐含的条件就是满射，说明它的最大匹配就是 N。之后再枚举每条边，删除后匹配一次，匹配减少了的话，说明这条是必须边了，找的同时输出即可。找不到则输出none。

 

       二分图必须边：

       二分图必须边就是二分图最大匹配所不能缺少的边。这道题有个条件就是，度为1的点或者区域所关联的边就是必须边，但是在其他题中就不一定是了。若其他题也要找必须边的话，要先最大匹配一次，后再枚举每条边再匹配，若匹配减少了则说明这条边是必须边。

    

       AC：

#include <cstdio>
#include <algorithm>
#include <string.h>
using namespace std;

int n;
int r[200][5],w[200][200];
int vis[200],linker[200];

bool dfs(int u) {
    for(int v = 1;v <= n;v++)
        if(w[u][v] && !vis[v]) {
            vis[v] = 1;
            if(linker[v] == -1 || dfs(linker[v])) {
                linker[v] = u;
                return true;
            }
        }
    return false;
}

int hungary() {
    int res = 0;
    memset(linker,-1,sizeof(linker));
    for(int u = 1;u <= n;u++) {
        memset(vis,0,sizeof(vis));
        if(dfs(u)) res++;
    }
    return res;
}

int main() {
    int time = 0;
    while(~scanf("%d",&n) && n) {
        ++time;
        memset(w,0,sizeof(w));

        for(int i = 1;i <= n;i++)
            for(int j = 1;j <= 4;j++)
                scanf("%d",&r[i][j]);

        for(int i = 1;i <= n;i++) {
            int x,y;
            scanf("%d%d",&x,&y);
            for(int j = 1;j <= n;j++)
                if(x >= r[j][1] &&
                   x <= r[j][2] &&
                   y >= r[j][3] &&
                   y <= r[j][4]) {
                   w[j][i] = 1;
                }
        }

        printf("Heap %d\n",time);
        int sum = 0;
        for(int i = 1;i <= n;i++)
            for(int j = 1;j <= n;j++) {
                if(w[i][j]) {
                   w[i][j] = 0;
                   if(hungary() < n) {
                        if(!sum) printf("(%c,%d)",'A' + i - 1,j);
                        else printf(" (%c,%d)",'A' + i - 1,j);
                        sum++;
                   }
                   w[i][j] = 1;
                }
            }

        if(!sum) printf("none\n\n");
        else printf("\n\n");
    }
    return 0;
}