空间参考系统
1.1 空间参考系相关概念
谈到空间参考系统的时候,我们会用到许多专业术语,诸如坐标(Coordinate)、坐标系(Coordinate System)、椭球体(Ellipsoid)、大地基准面(Datum)、投影(Projection)、坐标转换(Coordinate System Transformation)等。在许多的资料中,并没有准确地区分这些术语。例如:许多资料中会使用坐标系这个词来代表一个空间参考系统。为此,国际标准化组织在ISO 19111 – Geographic information – Spatial referencing by coordinates中对这些术语进行了定义,本章中我们使用的术语也遵循了ISO 19111。
下图显示了空间参考系统的抽象模型。坐标是用来描述一个位置的序列值,有时我们将这个序列称之为坐标元组(Coordinate Tuple),它引用了一个空间参考系统。空间参考系统是引用了一个基准面的坐标系。坐标系是一个抽象的数学概念,不绑定于任何物理对象,它定义了如何计算坐标空间中两个坐标之间的距离、角度等信息,如笛卡尔坐标系、极坐标等。基准面一般是指地球的基准面,当然也可以是其它对象的基准面。坐标操作(Coordinate Operation)可以用于将一个空间参考系的坐标值转换为另一个空间参考系的坐标值。在不同基准面之间进行的坐标变换称之为坐标转换(Transformation),在不同的地图投影和不同地区的坐标之间进行的坐标变换称之为坐标变换(Conversion)。
1.1.1 坐标系的类型
不同的空间参考系统使用了不同的坐标系统,下面我们介绍几种常用的坐标系统。
l 椭球体坐标系(Ellipsoidal Coordinate System):一种二维或三维的坐标系。如果是二维,使用经度和纬度表示某一坐标的位置;如果是三维,使用距离椭球体表面的垂直高度作为第三维。
l 笛卡尔坐标系(Cartesian Coordinate System):。一种一维、二维或三维的坐标系。如果为一维,那么它只包含一根轴;如果为二维或三维,通过相对于这些正交轴的距离来定位一个坐标。
l 球形坐标系(Spherical Coordinate System):一种三维的坐标系,它使用了一个到原点的距离和两个角度来定位一个坐标。
1.1.2 椭球体和基准面
为了在地球表面上确定一个准确的位置,我们必须知道地球本身的形状和大小。正如我们所知,地球不是一个完美的球体,更像是一个在轴附近发生扁平的椭球体。因而,为了实用化,经常用椭球体的形状来描述地球的形状。人们以假想的平均静止的海水面形成的“大地体”为参照,计算出近似的椭球体。地球椭球体有长半轴a和短半轴b之分,长半轴即赤道半径,短半轴即极半径。f=(a-b)/a为椭球体的扁率,表示椭球体的扁平程度。由此可见,地球椭球体的形状和大小取决于a、b、f 。因此,a、b、f被称为地球椭球体的三要素。
从1953年起我国参照前苏联采用的克拉索夫斯基(Krassovsky)椭球体建立了我国的北京54坐标系,1978年采用国际大地测量协会推荐的IAG 75地球椭球体建立了我国新的坐标系——西安80坐标系。目前全球定位系统(GPS)采用的是WGS84椭球体。
| 椭球体 |
长半轴(a) |
短半轴(b) |
| Krassovsky |
6378245 |
6356863.0188 |
| IAG 75 |
6378140 |
6356755.2882 |
| WGS 84 |
6378137 |
6356752.3142 |
基准面是地球的一个模型,它给出了坐标系统和地球之间的关联关系。通过以下的两点可以定义一个基准面。
1) 椭球体的大小和形状(长半轴a,短半轴b)。
2) 依据一个定位点,基于地球物理表面对椭球体进行定位。
基准面是利用特定椭球体对特定地区地球表面的逼近。如果把地球比做是“马铃薯”,表面凸凹不平,而地球椭球体就好比一个“鸭蛋”,那么按照我们前面的定义,基准面就定义了怎样拿这个“鸭蛋”去逼近“马铃薯”某一个区域的表面,X、Y、Z轴进行一定的偏移,并各自旋转一定的角度,大小不适当的时候就缩放一下“鸭蛋”,那么通过如上的处理必定可以达到很好的逼近地球某一区域的表面。因为不同的地区关心的位置不同,需要最大限度的贴合自己的那一部分,大地基准面就会不同。因此,全世界有许多地方和区域性的基准面。
由此,我们可以看到椭球体与基准面之间的关系是一对多的关系,也就是基准面是在椭球体基础上建立的,但椭球体不能代表基准面,同样的椭球体能定义不同的基准面。如前苏联的Pulkovo 1942、非洲索马里的Afgooye基准面都采用了Krassovsky椭球体,但它们的基准面显然是不同的。
许多商业的GIS系统中,基准面是通过当地基准面向WGS84的转换7参数来定义,即三个平移参数ΔX、ΔY、ΔZ表示两坐标原点的平移值;三个旋转参数εx、εy、εz表示当地坐标系旋转至与地心坐标系平行时,分别绕Xt、Yt、Zt的旋转角;最后是比例校正因子,用于调整椭球大小。
1.1.3 投影
投影是为解决不可展的椭球面描绘到平面上的矛盾,用几何透视方法或数学分析的方法,将地球上的点和线投影到可展的曲面(平面、园柱面或圆锥面)上,将此可展曲面展成平面,建立该平面上的点、线和地球椭球面上的点、线的对应关系。
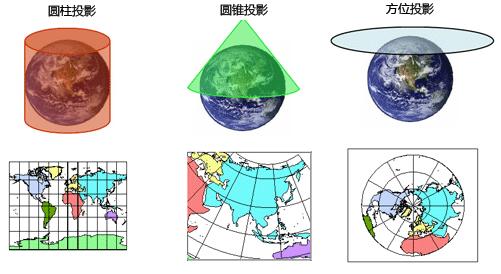
地图投影的过程是可以想象用一张足够大的纸去包裹地球,将地球上的地物投射到这张纸上。地球表面投影到平面上、圆锥面或者圆柱面上,然后把圆锥面、圆柱面沿母线切开后展成平面。根据这张纸包裹的方式,地图投影又可以分成:方位投影、圆锥投影和圆柱投影。根据这张纸与地球相交的方式,地图投影又可以分成切投影和割投影,在切线或者割线上的地物是没有变形的,而距离切线或者割线越远变形越大。
还有不少投影直接用解析法得到。根据所借助的几何面不同可分为伪方位投影、伪圆锥投影、伪圆柱投影等。
地图投影会存在两种误差,形状变化(也称角度变化)或者面积变化。投影以后能保持形状不变化的投影,称为等角投影 (Conformal Mapping),它的优点除了地物形状保持不变以外,在地图上测量两个地物之间的角度也能和实地保持一致,这非常重要,当在两地间航行必须保持航向的准确;或者另外一个例子是无论长距离发射导弹还是短距离发射炮弹,发射角度必须准确测量出来。因此等角投影是最常被使用的投影。等角投影的缺点是高纬度地区地物的面积会被放大。投影以后能保持形状不变化的投影,称为等面积投影 (Equivalent mapping),在有按面积分析需要的应用中很重要,显示出来的地物相对面积比例准确,但是形状会有变化,假设地球上有个圆,投影后绘制出来即变成个椭圆了。还有第三种投影,非等角等面积投影,意思是既有形状变化也有面积变化,这类投影既不等角也不等积,长度、角度、面积都有变形。其中有些投影在某个主方向上保持长度比例等于1,称为等距投影。
每一种投影都有其各自的适用方面。例如,墨卡托投影适用于海图,其面积变形随着纬度的增高而加大,但其方向变形很小;横轴墨卡托投影的面积变形随着距中央经线的距离的加大而增大,适用于制作不同的国家地图。等角投影常用于航海图、风向图、洋流图等。现在世界各国地形图采用此类投影比较多。等积投影用于绘制经济地区图和某些自然地图。对于大多数数学地图和小比例尺普通地图来说,应优先考虑等积的要求。地理区域,诸如国家、水域和地理分类地区(植被、人口、气候等)相对分布范围,显然是十分重要的内容。任意投影常用作数学地图,以及要求沿某一主方向保持距离正确的地图。常用作世界地图的投影有墨卡托投影、高尔投影、摩尔威特投影、等差分纬线多圆锥投影、格灵顿投影、桑森投影、乌尔马耶夫投影等。我国地形图所采用的高斯克吕格投影。
1.1.4 空间参考系的类型
在GIS中,应用最为普遍的空间参考系有:
l 地心参考系(Geocentric Reference System):以地球中心为原点,使用X、Y、Z来描述一个坐标值。
l 地理参考系(Geographic Reference System):它基于一个基准面,使用经度、纬度和高程描述一个坐标值。
l 投影参考系(Projected Reference System):它使用X(Easting)、Y(Northing)来描述地球上某个点的位置,单位米、英尺等。
地心参考系统基于笛卡尔坐标系统,以地球的中心为原点。z轴与地球旋转的轴共轴,在北极的方向上是正向;x轴穿过零度格林威治子午线;y轴与正向x和z轴形成直角。地心参考系统的优点在于它覆盖了整个地球,这也是它用于全球定位系统的原因。然而,地心参考系统只具有有限的实用性,当为了高程参考而引入椭球体时,我们只能获取椭球体高程,而这与通常国家高程系统中的表示方式是不一致的。
地理参考系统是基于椭球体坐标系,使用经度和纬度确定地球上任何一坐标的位置。如果我们将地球看作一个椭球体,而经纬网就是加在地球表面的地理坐标参照系格网,经度和纬度是从地球中心对地球表面给定点量测得到的角度。经度用位于格林威治子午线东面和西面的度数来表示,纬度用位于赤道平面的北面或南面的度数来表示。需要说明的是度不是标准的长度单位,不可用其量测长度。
1.1.5 高程参考
高程是定位地球上任何一点位置的重要部分。一个点的高程是它到所选择的参考表面的距离。通常,我们使用椭球体或大地水准面作为参照表面。因而,也有两种不同的垂直坐标系统。
l 正射高程系统:基于大地水准面给出高程。
l 球形高程系统:基于椭球体给出高程。
绝大多数国家都已经在正射高程系统的基础上建立了国家垂直参考系统,亦称之为垂直基准面。通常,一个高程系统的参照点是一检潮仪为基础,与全球标准上大偏差为1.0米的范围内的平均海平面相对应。这个贯穿所有零高程点的表面成为大地水准面。
1.2 空间参考系的表示
不同的GIS应用程序经常会使用不同的名称或代码代表相同的空间参考系统,这样会导致难于在不同的GIS系统间进行数据交换。所以,后来就出现了一些表示空间参考的标准。其中,最常用的要数EPSG代码和WKT。
1.2.1 EPSG代码
EPSG是欧洲石油勘探组织(European Petroleum Survey Group)的简称。在1985年,它创建了一个测量参数数据集(Geodetic Parameter Dataset)。1993年,它将这个数据集公布于众。2005年,欧洲石油勘测组织重组为国际油气生产者协会(International Association of Oil and Gas Producers,简称为OGP)勘探及定位委员会(Surveying and Positioning Committee)。现在,此数据集由国际油气生产者协会下属的测量委员会来维护。为了保持此数据集命名的连续性,所以现在仍然称之为ESPG测量参数数据集,简称为ESPG数据集。
ESPG数据集主要包含如下两方面的参数信息。
l 用来定义一个空间参考系统的参数。
l 坐标转换和坐标变换参数。
ESPG数据集由以下的三种方式发布。
l EPSG Registry:以Web的方式发布,用户可以通过http://www.epsg-registry.org/访问和查询此数据集。下面的表格是此网站生成的EPSG::4326的报告。
l EPSG Database:以关系数据库的方式发布。当前,它使用了在MS Access数据库,用户可以通过http://www.epsg.org/下载此数据库。
l SQL Scripts:以SQL脚本的方式发布,用户可以通过此SQL脚本在Oracle、MySQL等数据库中创建此数据集。
EPSG预留了从0到32767的整数用来对不同类型的椭球体、基准面、空间参考系统等参数进行编码,我们将这些整数称之为EPSG代码。通常情况下,我们所说的EPSG代码是指空间参考系统的代码。例如:EPSG::4326代表空间参考系统WGS 84。
1.2.2 WKT
WKT(Well-known Text)表示的空间参考系统是一种使用文字的方式表示的空间参考系统。正如大家所知,空间参考系统是由若干个子对象所组成。WKT使用一个大写的关键词来表示每一个对象,例如DATUM和UNIT。这些关键词之后跟着一些括号括起来的参数,参数之间使用逗号进行分割。OGC规定括号可以是圆括号“()”,也可以是方括号“[]”。一些对象是由其它对象所组成的,所以WKT(Well-known Text)表示的空间参考系统是一个嵌套的结构。
如下的扩展巴科斯范式(Extended Backus Naur Form,简称为EBNF)显示了定义一个WKT表示的空间参考系统的语法。
l 用于数学转换的子句。
| <math transform> |
= |
<param mt> | <concat mt> | <inv mt> | <passthrough mt> |
| <param mt> |
= |
PARAM_MT["<classification name>" {,<parameter>}* ] |
| <parameter> |
= |
PARAMETER["<name>", <value>] |
| <value> |
= |
<number> |
| <concat mt> |
= |
CONCAT_MT[<math transform> {,<math transform>}* ] |
| <inv mt> |
= |
INVERSE_MT[<math transform>] |
| <passthrough mt> |
= |
PASSTHROUGH_MT[<integer>, <math transform>] |
l 用于定义空间参考系统的子句。
| <coordinate system> |
= |
<horz cs> | <geocentric cs> | <vert cs> | <compd cs> | <fitted cs> | <local cs> |
| <horz cs> |
= |
<geographic cs> | <projected cs> |
| <projected cs> |
= |
PROJCS["<name>", <geographic cs>, <projection>, {<parameter>,}* <linear unit> {,<twin axes>}{,<authority>}] |
| <projection> |
= |
PROJECTION["<name>" {,<authority>}] |
| <geographic cs> |
= |
GEOGCS["<name>", <datum>, <prime meridian>, <angular unit> {,<twin axes>} {,<authority>}] |
| <datum> |
= |
DATUM["<name>", <spheroid> {,<to wgs84>} {,<authority>}] |
| <spheroid> |
= |
SPHEROID["<name>", <semi-major axis>, <inverse flattening> {,<authority>}] |
| <semi-major axis> |
= |
<number> |
| <inverse flattening> |
= |
<number> |
| <prime meridian> |
= |
PRIMEM["<name>", <longitude> {,<authority>}] |
| <longitude> |
= |
<number> |
| <angular unit> |
= |
<unit> |
| <linear unit> |
= |
<unit> |
| <unit> |
= |
UNIT["<name>", <conversion factor> {,<authority>}] |
| <conversion factor> |
= |
< 发表评论
最新评论
|






评论