无损联接分解
定义:无损联接分解是将一个关系模式分解成若干个关系模式后,通过自然联接和投影等运算仍能还原到原来的关系模式,则称这种分解为无损联接分解。
可还原
例1:关系模式:成绩(学号,姓名,课程号,课程名,分数)
函数依赖:学号->姓名,课程号->课程名, (学号,课程号)->分数
若将其分解为下面三个关系模式:
成绩(学号,课程号,分数)
学生(学号,姓名)
课程(课程号,课程名)
问,这样的分解是无损分解么?
----
由于:学号->姓名,所以:
成绩(
学号,课程号,分数,
姓名)
由于:课程号->课程名,所以:
成绩(学号,
课程号,分数,姓名,
课程名)
所以这个例子是无损分解
例2:设R=ABCDE, R1=AD,R2=BC,R3=BE,R4=CDE, R5=AE, 设函数依赖:
A->C, B->C, C->D, DE->C, CE->A. 判断R分解成
ρ={R1, R2, R3, R4, R5}是否无损联接分解?
解:
这样的题要通过画表的方法来解,首先,原始表:
|
|
A
|
B
|
C
|
D
|
E
|
|
AD
|
a1
|
b12
|
b13
|
a4
|
b15
|
|
BC
|
b21
|
a2
|
a3
|
b24
|
b25
|
|
BE
|
b31
|
a2
|
b33
|
b34
|
a5
|
|
CDE
|
b41
|
b42
|
a3
|
a4
|
a5
|
|
AE
|
a1
|
b52
|
b53
|
b54
|
a5
|
表
1
(A B C D E
是关系
R
的属性,
AD, BC, BE, CDE, AE
是分解之后每一个关系对应的属性集
)
填表的过程:
当横竖相交的时候,如果在分解关系中存在对应列的单个的属性(譬如第一列第一行AD与A相交的单元格,AD含有A,就填写a1),则填写
a
下标
, 下标就是单元格对应所在的列号。否则填写b下标, 下标是单元格对应所在的行列号。
填写之后的初始表就是表
1
所示
2.根据依赖关系修改原始表:
对于依赖关系A->C,看A列中有两行a1是相等的(第一行和第五行),所以在C列中对应的两行也应该相等,但是看到这两行都是b(b13,b53),所以将这个b都换成b13(上面的较小的标)
|
|
A
|
B
|
C
|
D
|
E
|
|
AD
|
a1
|
b12
|
b13
|
a4
|
b15
|
|
BC
|
b21
|
a2
|
a3
|
b24
|
b25
|
|
BE
|
b31
|
a2
|
b33
|
b34
|
a5
|
|
CDE
|
b41
|
b42
|
a3
|
a4
|
a5
|
|
AE
|
a1
|
b52
|
b53
à
b13
|
b54
|
a5
|
对于依赖BàC, 同样的道理,看B这一列中,第二行和第三行都是a2,那么对C这一列同样的操作,但是看到C这一列中第二行是a3,那么就将第三行改成a3,优先级比b要高。
|
|
A
|
B
|
C
|
D
|
E
|
|
AD
|
a1
|
b12
|
b13
|
a4
|
b15
|
|
BC
|
b21
|
a2
|
a3
|
b24
|
b25
|
|
BE
|
b31
|
a2
|
b33àa3
|
b34
|
a5
|
|
CDE
|
b41
|
b42
|
a3
|
a4
|
a5
|
|
AE
|
a1
|
b52
|
b13
|
b54
|
a5
|
对依赖CàD,C列的1,5行相等,D的1,5行也应该相等,D的第1行有a,所以b54换成a4;另外C列的2,3,4行也相等,D的2,3,4行也应该相等,D的第4行有a,所以将对应的行都换成a4
|
|
A
|
B
|
C
|
D
|
E
|
|
AD
|
a1
|
b12
|
b13
|
a4
|
b15
|
|
BC
|
b21
|
a2
|
a3
|
b24àa4
|
b25
|
|
BE
|
b31
|
a2
|
a3
|
b34àa4
|
a5
|
|
CDE
|
b41
|
b42
|
a3
|
a4
|
a5
|
|
AE
|
a1
|
b52
|
b13
|
b54àa4
|
a5
|
对于DEàC, DE公共的相等的行是3,4,5行,对应C的3,4,5行也应该相等,故将C列的两个的b13换成a3,所以表格经过这个函数依赖关系,就是:
|
|
A
|
B
|
C
|
D
|
E
|
|
AD
|
a1
|
b12
|
b13àa3
|
a4
|
b15
|
|
BC
|
b21
|
a2
|
a3
|
a4
|
b25
|
|
BE
|
b31
|
a2
|
a3
|
a4
|
a5
|
|
CDE
|
b41
|
b42
|
a3
|
a4
|
a5
|
|
AE
|
a1
|
b52
|
b13àa3
|
a4
|
a5
|
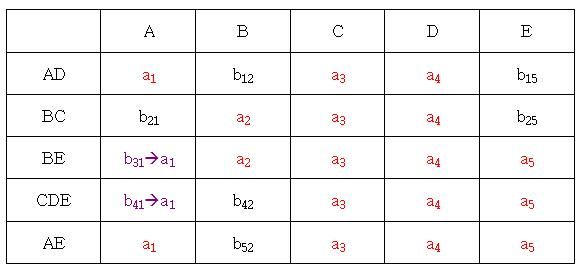
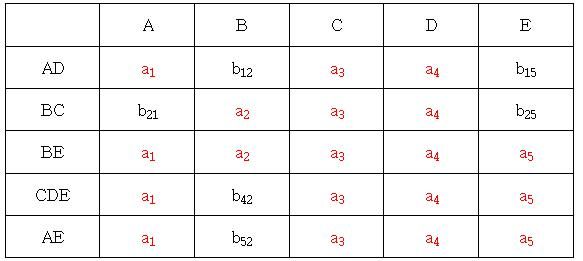
对于CEàA, CE的公共行是3,4,5行,所以将A的3,4,5行也对应相等,因为A列的第五行含有a1,所以将3,4行的b31,b41都换成a1
最终得到的表格就是:
最后,我们从表格里看到对于DE行来说,都是a,所以得出结论,题中的分解是无损联接分解
********************
无损分解的一个简便的判别方法(适用于分解成2个关系的情况)
譬如:
有关系R=ABC, 依赖关系{A-->B}那么下面哪个是无损分解:
A. {R1(AB),R2(AC)}
B.{R1(AB),R3(BC)}
首先看选项A,R1∩R2=A,R1-R2=B,R1 ∩ R2-->(R1-R2).所以它是无损分解
选项B, R1∩R2=B, R1-R2=A, R2-R1=C,
所以它不是无损分解
那么这里快速判断无损分解的方法就是
对两个集合先求集合的∩,然后求集合的差(2个集合有两个差的结果)
如果集合的∩-->集合的差(得到差结果的任意一个)成立那么就是无损分解
本文出自 “李骥平” 博客,请务必保留此出处http://fsjoy.blog.51cto.com/318484/137130