分类与聚类
首先分清聚类和分类的区别:
分类——监督学习算法,需要给定训练数据
聚类——无监督学习算法,无训练数据。
聚类分为 层次方法和非层次方法:
层次方法——最后形成一棵tree,每个node或者有k个分支,或者是叶子节点。( 过程似huffman tree)
非层次方法——是一个迭代过程,直至满足某个阀值退出。(主要包括k-mean 和 EM算法)
k-mean算法的步骤:(每个样本只能属于一个聚类)
1)随机选出k个centroid(质心)
2)将每个样本分配给与之距离最近的centroid
3)重新计算centroid
4)重复2) 3)直至centroid所对应的set不变
EM算法:(每个样本可以属于不同的聚类,但概率不同)
理论基础—计算极大似然估计,需要求似然函数的极值。输入是样本,但这个样本并不是完整数据,它只是观测数据。
完整数据(Z)包括观测数据(X)和未知数据(Y)。
log似然函数:ℓ ( θ; Z ) = log p( Z|θ)=log p( X,Y|θ)-----(1)
它的步骤跟EM所代表的单词有关,
<wbr><wbr><wbr><wbr>E——expectation,<br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>已知: 观测数据X,<span style="word-wrap:normal; word-break:normal; line-height:17px; font-size:11pt">参数θ的当前值</span><span style="word-wrap:normal; word-break:normal; line-height:17px; font-size:11pt">θt</span><br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><span style="word-wrap:normal; word-break:normal; line-height:17px; font-size:11pt">未知:Y<br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>对公式(1)求Y的期望,</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></span>得表达式Q(<span style="word-wrap:normal; word-break:normal; line-height:17px; font-size:11pt">θ,</span><span style="word-wrap:normal; word-break:normal; line-height:17px; font-size:11pt">θt</span>), Q中不含有变量Y。<br><wbr><wbr><wbr><wbr>M——maximization,对E步得到的Q(<span style="word-wrap:normal; word-break:normal; line-height:17px; font-size:11pt">θ,</span><span style="word-wrap:normal; word-break:normal; line-height:17px; font-size:11pt">θt</span>)求极大值,<br><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><span style="word-wrap:normal; word-break:normal; line-height:17px; font-size:11pt">即θt+1 =</span>argmax Q(<span style="word-wrap:normal; word-break:normal; line-height:17px; font-size:11pt">θ,</span><span style="word-wrap:normal; word-break:normal; line-height:17px; font-size:11pt">θt )</span><br><wbr><wbr><wbr><wbr>每次参数更新会增加非完整似然函数值<br><wbr><wbr><wbr><wbr>重复E、M两步,直至似然函数收敛到局部极大值。<br><br> EM会收敛到局部极值,但不保证收敛到全局最优;对初值很敏感,需要一个好的、快速的初始化过程。<br></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>
<wbr></wbr>
<wbr></wbr>
k-mean聚类算法如下:
1.<wbr><wbr><wbr><wbr><wbr><wbr>从数据点中,随机选取k个数据中心作为初始的聚类中心。例如k=3,则选择3个数据点</wbr></wbr></wbr></wbr></wbr></wbr>
2.<wbr><wbr><wbr><wbr><wbr><wbr>分别计算每一个点到k个中心点的距离(本文计算的是欧式距离),如果当前计算的数据点离第i个(i=1,2,…,k)中心点最近,则把当前点归到第i类.</wbr></wbr></wbr></wbr></wbr></wbr>
3.<wbr><wbr><wbr><wbr><wbr><wbr>重新计算k个聚类中心点。计算方式如下,如果第i类有n个数据点,则第i类新的中心为:</wbr></wbr></wbr></wbr></wbr></wbr>
<wbr><a href="http://photo.blog.sina.com.cn/showpic.html#blogid=48b8276f01013us7&url=http://s7.sinaimg.cn/orignal/48b8276ftc1ef8902ca86" target="_blank" style="text-decoration:none; color:rgb(27,113,155)"></a><br><a href="http://photo.blog.sina.com.cn/showpic.html#blogid=48b8276f01013us7&url=http://s3.sinaimg.cn/orignal/48b8276ftc1ef8bcd5472" target="_blank" style="text-decoration:none; color:rgb(27,113,155)"><img src="http://s3.sinaimg.cn/bmiddle/48b8276ftc1ef9044f7c3&690" name="image_operate_65101339134613281" alt="分类与聚类" title="分类与聚类" style="margin:0px; padding:0px; border:0px; list-style:none"></a><br><br><br></wbr>
<wbr><wbr><wbr><wbr>4.如果新的聚类中心跟上一次的聚类中心比较变化小于某值算法结束,否则转到第二步。</wbr></wbr></wbr></wbr>
聚类结果如下:
<wbr></wbr>
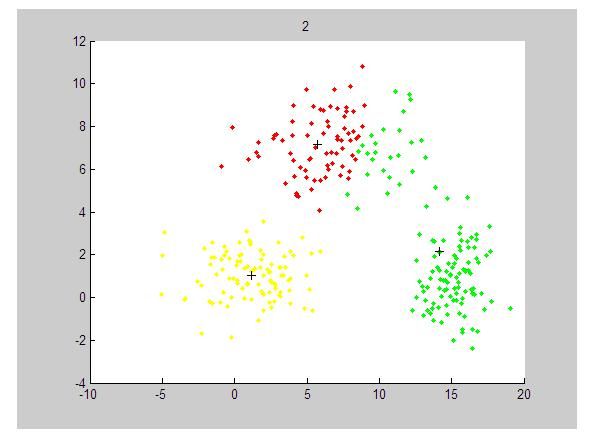
代码如下:http://download.csdn.net/source/3374443
load gaussdata; %由于我先前生成好了,直接load进来
maxiter = 50;<wbr><wbr>%设定最大频数</wbr></wbr>
iter = 1;
num = size(X,2);<wbr>%num为数据点个数</wbr>
index = randperm(num); %产生1到num个数字的一个随机排列
center = X(:,index(1:3)); %选择出3个初始的聚类中心
�nter = X(:,1:3);
old = center;<wbr><wbr><wbr><wbr><wbr><wbr>%记录旧的聚类中心</wbr></wbr></wbr></wbr></wbr></wbr>
<wbr></wbr>
hold on ;
plot(X(1,:),X(2,:),'g.');<wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>%绘制数据点</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>
plot(center(1,:),center(2,:),'ro'); %绘制数据中心
title(num2str(iter));<wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>%显示迭代步数</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>
hold off;
xnum = size(X,2);
cdim = size(center,2);
while iter<=maxiter
<wbr><wbr>clf;</wbr></wbr>
<wbr><wbr>hold on;</wbr></wbr>
<wbr><wbr>5-39行计算每一个点到k个中心的距离,一个很神奇的技巧,自己想吧,呵呵</wbr></wbr>
<wbr><wbr>sumX = sum(X.^2,1);</wbr></wbr>
<wbr><wbr>sumC = sum(center.^2,1);</wbr></wbr>
<wbr><wbr>XY = (2*X'*center)';</wbr></wbr>
<wbr><wbr>distance = repmat(sumX,cdim,1)+repmat(sumC',1,xnum)-XY;</wbr></wbr>
<wbr><wbr>[v,idx] = min(distance,[],1);<wbr><wbr>%求出数据点到哪一个中心的距离最近</wbr></wbr></wbr></wbr>
<wbr><wbr>Y = idx;<wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr><wbr>%对数据点进行分类</wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr></wbr>
<wbr><wbr>idx1 = find(idx==1);</wbr></wbr>
<wbr><wbr>idx2 = find(idx==2);</wbr></wbr>
<wbr><wbr>idx3 = find(idx==3);</wbr></wbr>
<wbr><wbr>%下面三行计算出新的聚类中心</wbr></wbr>
<wbr><wbr>center(:,1) = mean(X(:,idx1),2);</wbr></wbr>
<wbr><wbr>center(:,2) = mean(X(:,idx2),2);</wbr></wbr>
<wbr><wbr>center(:,3) = mean(X(:,idx3),2);</wbr></wbr>
<wbr><wbr>title(num2str(iter));</wbr></wbr>
<wbr><wbr>plot_data(X,Y,center);</wbr></wbr>
<wbr><wbr>hold off;</wbr></wbr>
<wbr><wbr>pause(0.1);</wbr></wbr>
<wbr><wbr>error = sum((center(:,1)-old(:,1)).^2,1);<wbr><wbr><wbr>%计算迭代中止条件</wbr></wbr></wbr></wbr></wbr>
<wbr><wbr>if error<0.000001</wbr></wbr>
<wbr><wbr><wbr><wbr><wbr>break;</wbr></wbr></wbr></wbr></wbr>
<wbr><wbr>end</wbr></wbr>
<wbr><wbr>old = center;</wbr></wbr>
<wbr><wbr>iter = iter+1;</wbr></wbr>
end