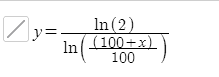编程珠玑--何为72法则
所谓的“72法则”就是以1%的复利来计息,经过72年以后,你的本金就会变成原来的一倍。这个公式好用的地方在于它能以一推十,例如:利用5%年报酬率的投资工具,经过14.4年(72/5)本金就变成一倍;利用12%的投资工具,则要6年左右(72/12),才能让1块钱变成2块钱。 因此,今天如果你手中有100万元,运用了报酬率15%的投资工具,你可以很快便知道,经过约4.8年,你的100万元就会变成200万元。
刚刚看到的时候感觉有点奇怪,这个72真的是正确的吗?72是怎么得到的呢?
在编程珠玑中看到,如果一个菌群中的细菌数量增长率为3%/小时,那么大概多长时间细菌的书目会翻番。答案就是72/3 =24小时。
自己也动手写了个简单的测试程序,随便修改增长率,得到的结果都基本上符合72法则。
/*****************
*验证72法则
******************/
#include <stdio.h>
double gain(double rate,double capital)
{
return ((double)(100+rate) * capital)/(double)100;
}
int main()
{
int i;
double rate;//增长率% rate/100.0
double capital = 2000;
double gole = 2 * capital;
rate = 3;
for(i = 1;capital <= gole; ++i)
{
capital = gain(rate,capital);
printf("第%d年\t总收益:%g\n",i,capital);
}
return 0;
}
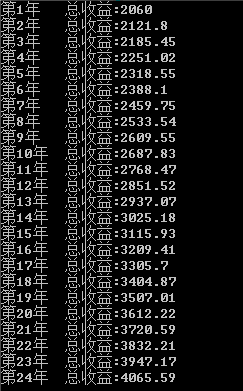
虽然利用72法则不像查表计算那么精确,但也已经十分接近了,因此当你手中少了一份复利表时,记住简单的 72法则,或许能够帮你不少的忙。
那么这72法则的原理是什么呢?
这个问题就是定期存款复利的问题。
下面从数学的角度来大体计算一下:
定期复利的将来值(FV)为:
FV = PV * (1+r)^t
当中PV为现在值、t为期数、r为每一期的利率。
当该笔投资倍增,则FV = 2PV。代入上式后,可简化为:
2 = (1+r)^t
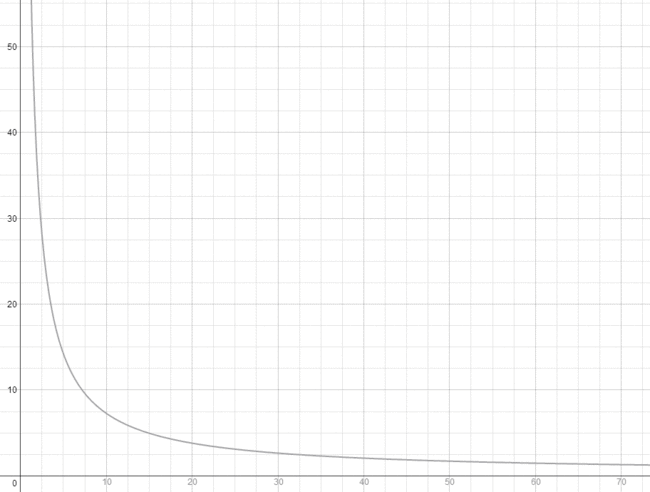
解方程得,t = ln2 ÷ ln(1+r),由软件将表达式画出来的结果如下:
若r数值较小,则ln(1+r)约等于r(这是泰勒级数的第一项),
而ln2 ≈ 0.693147,于是:
t ≈ 0.693147 ÷ r
其实在利率较小的情况下是由69.3会更加准确,但是由于72的因子比较多,估计计算的时候相对容易计算,所以选择了72。