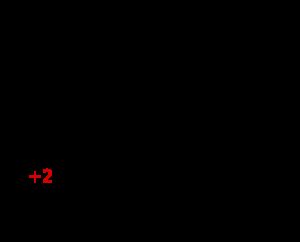“Sketching” data structures store a summary of a data set in situations where the whole data would be prohibitively costly to store (at least in a fast-access place like the memory as opposed to the hard disk). Variants of trees, hash tables, etc. are not sketching structures, they just facilitate access to the data, but they still store the data itself. However, the concept of hashing is closely related to most sketching ideas as we will see.
The main feature of sketching data structures is that they can answer certain questions about the data extremely efficiently, at the price of the occasional error. The best part is that the probability of an error can be quantified and the programmer can trade off the expected error rate with the amount of resources (storage, time) afforded. At the limit of this trade-off (when no error is allowed) these sketching structures collapse into traditional data structures.
Sketching data structures are somewhat counter-intuitive, but they can be useful in many real applications. I look at two such structures mostly for my own benefit: As I try to understand them, I write down my notes. Perhaps someone else will find them useful. Links to further information can be found in the end. Leave comments if you know of other sketching data structures that you found useful or if you have some favorite elegant and unusual data structure.
The Count-Min (CM) sketch is less known than the Bloom filter, but it is somewhat similar (especially to the counting variants of the Bloom filter). The problem here is to store a numerical value associated with each element, say the number of occurrences of the element in a stream (for example when counting accesses from different IP addresses to a server). Surprisingly, this can be done using less space than the number of elements, with the trade-off that the result can be slightly off sometimes, but mostly on the small values. Again, the parameters of the data structure can be chosen such as to obtain a desired accuracy.
CM works as follows: we have k different hash functions and k different tables which are indexed by the outputs of these functions (note that the Bloom filter can be implemented in this way as well). The fields in the tables are now integer values. Initially we have all fields set to 0 (all unseen elements have count 0). When we increase the count of an element, we increment all the corresponding k fields in the different tables (given by the hash values of the element). If a decrease operation is allowed (which makes things more difficult), we similarly subtract a value from all k elements.
To obtain the count of an element, we take the minimum of the k fields that correspond to that element (as given by the hashes). This makes intuitive sense. Out of the k values, probably some have been incremented on other elements also (if there were collisions on the hash values). However, if not all k fields have been returned by the hash functions on other elements, the minimum will give the correct value. See illustration for an example on counting hits from IP addresses:
In this example the scenario could be that we want to notice if an IP address is responsible for a lot of traffic (to further investigate if there is a problem or some kind of attack). The CM structure allows us to do this without storing a record for each address. When we increment the fields corresponding to an address, simultaneously we check if the minimum is above some threshold and we do some costly operation if it is (which might be a false alert). On the other hand, the real count can never be larger than the reported number, so if the minimum is a small number, we don’t have to do anything (this holds for the presented simple variant that does not allow decreases). As the example shows, CM sketch is most useful for detecting “heavy hitters” in a stream.
It is interesting to note that if we take the CM data structure and make the counters such that they saturate at 1, we obtain the Bloom filter.
Refrences
http://en.wikipedia.org/wiki/Count%E2%80%93min_sketch
http://research.neustar.biz/2011/09/08/our-approach/
http://lkozma.net/blog/sketching-data-structures/
http://research.neustar.biz/tag/count-min-sketch/