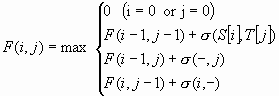SMITH WATERMAN算法
1.1 序列相似性比较
生物信息学中,对各种生物大分子序列进行分析是一件非常基本的工作。从序列的片段测定,拼接,基因的表达分析,到RNA和蛋白质的结构功能预测,物种亲缘树的构建都需要进行生物分子序列相似性的比较。在遗传物质长期的演化过程中,原本相同的DNA序列由于其中一条序列缺失了几个片断,或增加了几个片断,或某段子序列发生了位置的变化等,从而导致他们发生了不同,这两条序列不一定能进行精确的匹配,但是他们有一定的相似度。我们应该如何判定序列之间的这种相似性?对于这种情况,生物学家提出了一种用来评定序列相似性的方法,称为记分函数的方法。
定义1:如果![]() 是一个序列,那么
是一个序列,那么![]() 表示
表示![]() 中的字符长度,
中的字符长度,![]() 表示序列的第
表示序列的第![]() 个字符。如果序列
个字符。如果序列![]() 和序列
和序列![]() 相同,必须满足如下条件:
相同,必须满足如下条件:
(1)、![]() ;
;
(2)、![]() ;
;
定义2:如果![]() 和
和![]() 是两个字符,那么
是两个字符,那么![]() 表示
表示![]() 和
和![]() 字符在进行比较时所得的分值,
字符在进行比较时所得的分值,![]() 称为一个记分函数,记分函数还包括当
称为一个记分函数,记分函数还包括当![]() 为空字符或
为空字符或![]() 为空字符的情况,在序列中一个所谓的空字符表示序列中空字符的位置可能缺失一个未知的字符,我们只能使用空字符来表示这种缺失;
为空字符的情况,在序列中一个所谓的空字符表示序列中空字符的位置可能缺失一个未知的字符,我们只能使用空字符来表示这种缺失;
定义3:如果![]() 和
和![]() 是两个序列,那么
是两个序列,那么![]() 的一个相似性比较
的一个相似性比较![]() 可以用
可以用![]() 和
和![]() 来表示,其中:
来表示,其中:
(1)、![]() ;
;
(2)、将![]() 和
和![]() 中的空字符除去后所得的序列分别和
中的空字符除去后所得的序列分别和![]() 、
、![]() 相同;
相同;
相似性比较![]() 就是
就是![]() 和
和![]() 中字符一一比对,相似性比较
中字符一一比对,相似性比较![]() 的得分
的得分![]() 可以用如下公式表示:
可以用如下公式表示:
其中![]() ;
;
定义4:对于两个序列![]() 和
和![]() ,它们的最优相似性比较
,它们的最优相似性比较![]() 是指在
是指在![]() 和
和![]() 的所有相似性比较中得分最高的一个,序列相似性比较算法的主要目标就是如何寻找出序列间的最优相似性比较。
的所有相似性比较中得分最高的一个,序列相似性比较算法的主要目标就是如何寻找出序列间的最优相似性比较。
|
|
1 |
2 |
|
i-1 |
I |
| 1 |
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
| j-1 |
|
|
|
|
|
| J |
|
|
|
|
|
1.2 Smith Waterman算法
在寻找序列最优相似比较的算法中有两种算法使用最为广泛:Blast算法和Smith Waterman算法,Blast算法的运行速度要比Smith Waterman算法快,但是Smith Waterman算法要比BLAST算法更为精确。Smith Waterman算法先用迭代方法计算出两个序列的所有可能相似性比较的分值,然后通过动态规划的方法回溯寻找最优相似性比较。
Smith Waterman算法的具体描述如下:
对于两个序列![]() 和
和![]() ,
,![]() 和
和![]() ,其中
,其中![]() ,都属于某个字符集
,都属于某个字符集![]() ,对
,对![]() 中的任何元素和空符号,他们两两之间都有一个记分值,用记分函数
中的任何元素和空符号,他们两两之间都有一个记分值,用记分函数![]() 表示,
表示,![]() 表示序列
表示序列![]() 的前缀
的前缀![]() 和序列
和序列![]() 的前缀
的前缀![]() 之间的最优相似性比较的得分。那么有如下公式:
之间的最优相似性比较的得分。那么有如下公式:
通过公式我们可以得到如下的一个得分矩阵![]() :
:
通过得分矩阵进行动态规划回溯法获得相似性比较的算法如下:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
其中![]() 函数表示在一个序列b的第c个位置插入一个字符a
函数表示在一个序列b的第c个位置插入一个字符a
Smith Waterman算法中,假设![]() ,
,![]() , 在开始计算得分矩阵
, 在开始计算得分矩阵![]() 时需要计算矩阵的每一个得分值,计算复杂度为
时需要计算矩阵的每一个得分值,计算复杂度为![]() 。从上面的回溯算法中可以看到,第二步回溯算法的计算复杂度为
。从上面的回溯算法中可以看到,第二步回溯算法的计算复杂度为![]() 。这样Smith Waterman算法的整体时间复杂度为
。这样Smith Waterman算法的整体时间复杂度为![]() 。使用Smith Waterman算法计算两个序列最大相似性比较时绝大部分计算时间将消耗在计算得分矩阵上
。使用Smith Waterman算法计算两个序列最大相似性比较时绝大部分计算时间将消耗在计算得分矩阵上![]() 。
。
的值。当![]() ,
,![]() 和
和![]() 已经计算出来后,我们称
已经计算出来后,我们称![]() 是可计算的。如下图所示:
是可计算的。如下图所示:
| a | t | g | c | ||
| 0 | 1 | 2 | 3 | -> | |
| a | 1 | 0 | 1 | -> | |
| t | 2 | 1 | -> | ||
| g | 3 | -> | |||
| c | -> |
图中“->”表示该矩阵元素当时可计算
通过上图的分析,在某个特定的时候,矩阵中出现多个可以同时计算的元素,实际上就是在计算得分矩阵的过程中包含着可并行性。Smith Waterman算法就可以利用这种并行性进行并行优化。 一般来说,类似于Smith Waterman算法这种具有明显数据依赖和迭代的算法最适合于在数据流模型的并行计算机上进行并行化,但是这种数据流模型的计算机仅仅作为一种模型存在,这种体系结构的计算机现在并不存在。