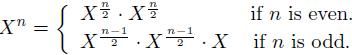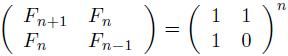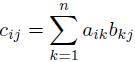算法导论Lecture 3:分治法
Lecture 3真得很重要,因为Divide and Conquer思想很重要。本课又是Erik主讲。听了70多分钟,写了6页的Notes,现在整理一下。
分治(Divide and conquer, or divide et impera)
分治法是非常基本但却很强大的算法设计技巧。这也是这个课程的几个设计技巧中的第一个。分治法将会用到很多的递归技术,也就是前面两课中着重讲到的。
分治法有三个步骤:
- Divide the problem into a number of subproblems
- Conquer the subproblems by solving them recursively. // 如果问题足够小就直接解决
- Combine the solutions to the subproblems into the solution for the original problem.
我们已经说过的利用分治思想的算法有Merge sort, Binary search。Erik又额外讲了四个利用分治思想的例子。
数的幂乘(Powering a number) 给定一个数X和一个整数n>=0,计算X^n。
直接的解法就是将X乘上n次,需要Theta(n)。我们可以使用分治的思想,将n个X的乘法分成2个X^(n/2)的子问题,并递归的求出X^(n/2)。
递归式为T(n) = T(n/2) + Theta(1)。用主方法可以解得T(n) = Theta(lgn)。
斐波纳契数(Fibonacci Numbers) 斐波纳契数定义如下式,给定非负整数n,求第n个Fibonacci数。
最原始的方法是使用直接使用这个递归式,即递归地求出F_{n-1},F_{n-2},注意到求F_{n-1}的时候会重复地计算F_{n-2},所以这种原始的算法开销是很大的,如果你熟悉斐波纳契数的通项的话你应该知道这个算法是个指数算法,需要Theta(phi^n),phi = (1+sqrt(5))/2 > 1。可以讲指数算法几乎是没什么用的,你可以写出这个算法的代码,但是当n变得的稍大一点你的堆栈就要开始抱怨了,当然前提是你使用的语言的确是使用堆栈来传递参数的。即使你的语言不使用堆栈或者有什么优化能避免堆栈溢出,你也等不了那么长的时间,程序员一般都是看起来文静但实际上却很急躁的...尤其是在等待程序运行结果的时候。
当然我们可以换一种思路,比如采用自低向上的方法来计算出每一个F_i,一直到F_n,这要用到一点点缓存,但是算法的时间与n成比例,即我们可以在线性时间内来计算F_n。
或者可以有另一种想法,我们可以利用斐波纳契数的一个性质:F_n = phi^n / sqrt(5) rounded to the nearest integer,即计算phi^n/sqrt(5)然后四舍五入即得F_n,计算phi^n的时候也许可以用上面的数的幂乘技巧来提高效率Theta(lg n)。但是实际上这也是不实用的(impractical),由于精度的原因,我们使用的机器模型不适合处理这样的有理数。当n很大的时候,机器的舍入部分会使得结果不正确。
还有一种方法不仅实用,而且可以将时间约束在Theta(lg n)内。还是使用前面的幂乘技巧,但是我们转而处理整数而不是有理数。注意到斐波纳契数的一个性质:
这个式子可以用归纳法证明。前面数的幂乘的方法可以推广到矩阵的幂乘上,每一步的操作仍然是Theta(1),只是这个常数比数乘中稍大一些,数乘只有一个操作,而这里的2*2矩阵乘需要8个乘法和4个加法。不管怎么样,这个开销仍然是一个常数。也就是T(n) = T(n/2) + Theta(1),T(n) = Theta(lg(n))。
矩阵乘(Matrix Multiplication) 将两个n*n的方阵相乘。
输入:A=[a_{i,j}], B=[b_{i,j}], i,j = 1, 2, ... , n.
输出:C=[c_{i,j}] = AB, 也就是
原始的方法是将每一项相乘再相加求得c_{i,j},这需要Theta(n^3)的时间。如果我们使用分治法来设计算法,最直观的想法是将矩阵划成块:n*n matrix=2*2 block matrix of n/2 * n/2 submatrices。Like this:
其中r = ae+bg, s = af + bh, t = ce + dg, u = cf+dh。我们需要8个矩阵乘和4个矩阵加法,8个矩阵乘用递归来解,而4个矩阵加是非递归的工作,需要Theta(n^2)的时间。所以T(n) = 8T(n/2) + Theta(n^2),解得T(n) = Theta(n^3)。啊!这样做似乎并没有什么提升,是的,这还是一个3阶多项式时间的算法。
Strassen's algorithms
注意到在解上面这个递归式T(n) = 8T(n/2) + Theta(n^2)的时候,由于我们有8个矩阵乘,所以渐近时间是由n^3=n^(lg8)来控制的,如果我们能将乘法减少一点呢?Strassen算法的思想就是将8个矩阵乘消到7个,加法操作仍然是Theta(n^2)。这7个乘法如下:
p1 = a(f-h)
p2 = (a+b)h
p3 = (c+d)e
p4 = d(g-e)
p5 = (a+d)(e+h)
p6 = (b-d)(g+h)
p7 = (a-c)(e+f)
剩下的是加(减)法:
r = p5 + p4 - p2 + p6
s = p2 + p1
t = p3 + p4
u = p2 + p1 - p3 - p7
如果你读到这里了,就拿笔验证一下上面的式子吧,Erik说:“Strassen就是Strassen。”他如何才能想到会这样去做矩阵乘呢?早在1969年的时候Volker Strassen就发表了他的算法,尽管这个算法只比标准的矩阵乘快那么一点点,但他是第一个指出标准矩阵乘不是最优的(Strassen, Volker, Gaussian Elimination is not Optimal, Numer. Math. 13, p. 354-356, 1969)。他的这篇论文也开启了人们对更快的矩阵乘算法的寻找工作(在这之前人们是很难想像标准算法还是能再提高的),比如1987年出现的Coppersmith-Winogard算法,这一算法也是直到现在所知的渐近最快的算法。
我们来算一下Strassen算法的渐近运行时间:T(n) = 7T(n/2) + Theta(n^2),用主方法可知T(n) = Theta(n^(lg7)),lg7大概为2.81,因此T(n)=O(n^2.81)。上面提到的Coppersmith–Winograd算法是O(n^2.376)。我们应该能看出矩阵乘算法的一个下界:Omega(n^2),因为C中有n^2个元素要计算。2.376和2之间仍然有很大的空间,我相信人们仍然在寻找着更快的算法,谁也不知道这样的算法存不存在, who knows?
最后一个例子是VLSI布局问题,只是用到了Divide and conquer的思想而不是算法。不写了。